Difference between revisions of "Thue-Mahler equation"
(Importing text file) |
m (Automatically changed introduction) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 50 formulas, 49 were replaced by TEX code.--> | |
| − | in | + | {{TEX|semi-auto}}{{TEX|part}} |
| + | Let $F ( X , Y ) \in \mathbf{Z} [ X , Y ]$ be a [[Binary form|binary form]] of degree $r \geq 3$, irreducible over $\mathbf{Q}$, let $S = \{ p _ { 1 } , \dots , p _ { s } \}$ be a fixed set of rational prime numbers and let $a \neq 0$ be a fixed rational integer. The Diophantine equation (cf. also [[Diophantine equations|Diophantine equations]]) | ||
| − | + | \begin{equation} \tag{a1} F ( x , y ) = a p _ { 1 } ^ { z _ { 1 } } \dots p _ { s } ^ { z _ { s } } \end{equation} | |
| − | is called a | + | in the unknowns $x , y , z _ { 1 } , \dots , z _ { s } \in \mathbf{Z}$, with $x$ and $y$ relatively prime, is called a Thue–Mahler equation. More generally, let $K$ be an algebraic number field (cf. [[Number field|Number field]]; [[Algebraic number|Algebraic number]]), let $S$ be a fixed finite set of places in $K$ (cf. also [[Place of a field|Place of a field]]), containing all infinite ones, let $\mathcal{O} _ { S }$ be the ring of $S$-integers and let $\mathcal{O} _ { S } ^ { * }$ be the group of $S$-units of $K$. Let $F ( X , Y ) \in O _ { S } [ X , Y ]$ be a binary form of degree $r \geq 3$, irreducible over $K$. The Diophantine equation |
| − | + | \begin{equation} \tag{a2} F ( x , y ) \in \mathcal{O} _ { S } ^ { * }\quad \text { in} ( x , y ) \in \mathcal{O} _ { S } \times \mathcal{O} _ { S } \end{equation} | |
| − | + | is called a generalized Thue–Mahler equation. If $a, p _ { 1 } , \dots , p _ { s }$ are as in (a1) and one takes in (a2) $K = \mathbf{Q}$ and $S = \{ p _ { 1 } , \dots , p _ { s } \} \cup \{ p : p \text{ is prime and divides } a\}$, then all solutions of (a1) are also solutions of (a2). Hence, any result concerning the solutions of (a1) applies also to those of (a2). | |
| − | + | In 1933, K. Mahler, using his $p$-adic analogues of the methods of A. Thue [[#References|[a7]]] and C.L. Siegel [[#References|[a5]]], proved in [[#References|[a3]]] that a Thue–Mahler equation (a1) has at most finitely many solutions. Because of the applied methods, this result is non-effective, i.e. it does not imply an explicit bound for either the size of the unknowns, or for the number of solutions. The development of Baker's theory (cf. also [[Gel'fond–Baker method|Gel'fond–Baker method]]) and its $p$-adic analogues made possible, in the 1970s, the proof of effective, though not explicit, bounds for the size of the unknowns; see [[#References|[a4]]], Chap. 7. Subsequently, very explicit upper bounds for | |
| − | + | \begin{equation*} \operatorname { max } \{ | x | , | y | , p _ { 1 } ^ { z _ { 1 } } \ldots p _ { s } ^ { z _ { s } } \} \end{equation*} | |
| − | In the early 1990s, constructive methods for the explicit computation of all solutions of a Thue–Mahler equation (a1) were developed by N. Tzanakis and B.M.M. de Weger [[#References|[a8]]], [[#References|[a9]]]. These are based on the theory (real and complex as well as | + | have been proved. A characteristic result of this type is due to Y. Bugeaud and K. Gőry [[#References|[a1]]], in which the quantities $s$, $a$, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120080/t12008030.png"/>, $r$, $H$, $h$, $R$ are involved; here, $H > 3$ is an upper bound for the absolute values of the coefficients of $F$ and $h$, $R$ are, respectively, the class number and the regulator of the number field generated (over $\mathbf{Q}$) by a root of the polynomial $F ( X , 1 )$ (cf. also [[Class field theory|Class field theory]]). |
| + | |||
| + | Due to techniques in [[Diophantine approximations|Diophantine approximations]], explicit upper bounds for the number of essentially distinct solutions have been proved for (a2), where two solutions $( x _ { 1 } , y _ { 1 } )$, $( x _ { 2 } , y _ { 2 } )$ are considered as essentially distinct if $( x _ { 2 } , y _ { 2 } )$ is not of the form $( \epsilon x _ { 1 } , \epsilon y _ { 1 } )$ for some $\epsilon \in \mathcal{O} _ { S } ^ { * }$. In view of the observation following (a2), such a bound is also valid for the number of solutions of (a1). Thus, Mahler's finiteness result has been considerably generalized and, what is more, in an explicit form. A characteristic result of this type is due to J.-H. Evertse [[#References|[a2]]]: Let the cardinality of $S$ in (a2) be $s$. Then, the number of essentially distinct solutions $( x , y ) \in \mathcal{O} _ { S } \times \mathcal{O} _ { S }$ is at most $( 5 \times 10 ^ { 6 } r ) ^ { s }$. | ||
| + | |||
| + | In the early 1990s, constructive methods for the explicit computation of all solutions of a Thue–Mahler equation (a1) were developed by N. Tzanakis and B.M.M. de Weger [[#References|[a8]]], [[#References|[a9]]]. These are based on the theory (real and complex as well as $p$-adic) of linear forms in logarithms of algebraic numbers (cf. [[Linear form in logarithms|Linear form in logarithms]]) and reduction techniques, like the LLL-basis reduction algorithm and the computation of "small" vectors in a lattice (cf. also [[LLL basis reduction method|LLL basis reduction method]]). This method can, in principle, be extended to equations of the form (a2), as shown by N.P. Smart in [[#References|[a6]]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> Y. Bugeaud, K. Győry, "Bounds for the solutions of Thue–Mahler equations and norm form equations" ''Acta Arith.'' , '''74''' (1996) pp. 273–292</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> J.-H. Evertse, "The number of solutions of the Thue–Mahler equation" ''J. Reine Angew. Math.'' , '''482''' (1997) pp. 121–149</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> K. Mahler, "Zur Approximation algebraischer Zahlen, I: Ueber den grössten Primteiler binärer Formen" ''Math. Ann.'' , '''107''' (1933) pp. 691–730</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> T.N. Shorey, R. Tijdeman, "Exponential Diophantine equations" , ''Tracts in Math.'' , '''87''' , Cambridge Univ. Press (1986)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> C.L. Siegel, "Approximation algebraischer Zahlen" ''Math. Z.'' , '''10''' (1921) pp. 173–213</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> N.P. Smart, "Thue and Thue–Mahler equations over rings of integers" ''J. London Math. Soc.'' , '''56''' : 2 (1997) pp. 455–462</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> A. Thue, "Ueber Annäherungswerte algebraischer Zahlen" ''J. Reine Angew. Math.'' , '''135''' (1909) pp. 284–305</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> N. Tzanakis, B.M.M. de Weger, "Solving a specific Thue–Mahler equation" ''Math. Comp.'' , '''57''' (1991) pp. 799–815</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> N. Tzanakis, B.M.M. de Weger, "How to explicitly solve a Thue–Mahler equation" ''Compositio Math.'' , '''84''' (1992) pp. 223–288</td></tr></table> |
Revision as of 17:46, 1 July 2020
Let $F ( X , Y ) \in \mathbf{Z} [ X , Y ]$ be a binary form of degree $r \geq 3$, irreducible over $\mathbf{Q}$, let $S = \{ p _ { 1 } , \dots , p _ { s } \}$ be a fixed set of rational prime numbers and let $a \neq 0$ be a fixed rational integer. The Diophantine equation (cf. also Diophantine equations)
\begin{equation} \tag{a1} F ( x , y ) = a p _ { 1 } ^ { z _ { 1 } } \dots p _ { s } ^ { z _ { s } } \end{equation}
in the unknowns $x , y , z _ { 1 } , \dots , z _ { s } \in \mathbf{Z}$, with $x$ and $y$ relatively prime, is called a Thue–Mahler equation. More generally, let $K$ be an algebraic number field (cf. Number field; Algebraic number), let $S$ be a fixed finite set of places in $K$ (cf. also Place of a field), containing all infinite ones, let $\mathcal{O} _ { S }$ be the ring of $S$-integers and let $\mathcal{O} _ { S } ^ { * }$ be the group of $S$-units of $K$. Let $F ( X , Y ) \in O _ { S } [ X , Y ]$ be a binary form of degree $r \geq 3$, irreducible over $K$. The Diophantine equation
\begin{equation} \tag{a2} F ( x , y ) \in \mathcal{O} _ { S } ^ { * }\quad \text { in} ( x , y ) \in \mathcal{O} _ { S } \times \mathcal{O} _ { S } \end{equation}
is called a generalized Thue–Mahler equation. If $a, p _ { 1 } , \dots , p _ { s }$ are as in (a1) and one takes in (a2) $K = \mathbf{Q}$ and $S = \{ p _ { 1 } , \dots , p _ { s } \} \cup \{ p : p \text{ is prime and divides } a\}$, then all solutions of (a1) are also solutions of (a2). Hence, any result concerning the solutions of (a1) applies also to those of (a2).
In 1933, K. Mahler, using his $p$-adic analogues of the methods of A. Thue [a7] and C.L. Siegel [a5], proved in [a3] that a Thue–Mahler equation (a1) has at most finitely many solutions. Because of the applied methods, this result is non-effective, i.e. it does not imply an explicit bound for either the size of the unknowns, or for the number of solutions. The development of Baker's theory (cf. also Gel'fond–Baker method) and its $p$-adic analogues made possible, in the 1970s, the proof of effective, though not explicit, bounds for the size of the unknowns; see [a4], Chap. 7. Subsequently, very explicit upper bounds for
\begin{equation*} \operatorname { max } \{ | x | , | y | , p _ { 1 } ^ { z _ { 1 } } \ldots p _ { s } ^ { z _ { s } } \} \end{equation*}
have been proved. A characteristic result of this type is due to Y. Bugeaud and K. Gőry [a1], in which the quantities $s$, $a$, 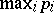 , $r$, $H$, $h$, $R$ are involved; here, $H > 3$ is an upper bound for the absolute values of the coefficients of $F$ and $h$, $R$ are, respectively, the class number and the regulator of the number field generated (over $\mathbf{Q}$) by a root of the polynomial $F ( X , 1 )$ (cf. also Class field theory).
, $r$, $H$, $h$, $R$ are involved; here, $H > 3$ is an upper bound for the absolute values of the coefficients of $F$ and $h$, $R$ are, respectively, the class number and the regulator of the number field generated (over $\mathbf{Q}$) by a root of the polynomial $F ( X , 1 )$ (cf. also Class field theory).
Due to techniques in Diophantine approximations, explicit upper bounds for the number of essentially distinct solutions have been proved for (a2), where two solutions $( x _ { 1 } , y _ { 1 } )$, $( x _ { 2 } , y _ { 2 } )$ are considered as essentially distinct if $( x _ { 2 } , y _ { 2 } )$ is not of the form $( \epsilon x _ { 1 } , \epsilon y _ { 1 } )$ for some $\epsilon \in \mathcal{O} _ { S } ^ { * }$. In view of the observation following (a2), such a bound is also valid for the number of solutions of (a1). Thus, Mahler's finiteness result has been considerably generalized and, what is more, in an explicit form. A characteristic result of this type is due to J.-H. Evertse [a2]: Let the cardinality of $S$ in (a2) be $s$. Then, the number of essentially distinct solutions $( x , y ) \in \mathcal{O} _ { S } \times \mathcal{O} _ { S }$ is at most $( 5 \times 10 ^ { 6 } r ) ^ { s }$.
In the early 1990s, constructive methods for the explicit computation of all solutions of a Thue–Mahler equation (a1) were developed by N. Tzanakis and B.M.M. de Weger [a8], [a9]. These are based on the theory (real and complex as well as $p$-adic) of linear forms in logarithms of algebraic numbers (cf. Linear form in logarithms) and reduction techniques, like the LLL-basis reduction algorithm and the computation of "small" vectors in a lattice (cf. also LLL basis reduction method). This method can, in principle, be extended to equations of the form (a2), as shown by N.P. Smart in [a6].
References
| [a1] | Y. Bugeaud, K. Győry, "Bounds for the solutions of Thue–Mahler equations and norm form equations" Acta Arith. , 74 (1996) pp. 273–292 |
| [a2] | J.-H. Evertse, "The number of solutions of the Thue–Mahler equation" J. Reine Angew. Math. , 482 (1997) pp. 121–149 |
| [a3] | K. Mahler, "Zur Approximation algebraischer Zahlen, I: Ueber den grössten Primteiler binärer Formen" Math. Ann. , 107 (1933) pp. 691–730 |
| [a4] | T.N. Shorey, R. Tijdeman, "Exponential Diophantine equations" , Tracts in Math. , 87 , Cambridge Univ. Press (1986) |
| [a5] | C.L. Siegel, "Approximation algebraischer Zahlen" Math. Z. , 10 (1921) pp. 173–213 |
| [a6] | N.P. Smart, "Thue and Thue–Mahler equations over rings of integers" J. London Math. Soc. , 56 : 2 (1997) pp. 455–462 |
| [a7] | A. Thue, "Ueber Annäherungswerte algebraischer Zahlen" J. Reine Angew. Math. , 135 (1909) pp. 284–305 |
| [a8] | N. Tzanakis, B.M.M. de Weger, "Solving a specific Thue–Mahler equation" Math. Comp. , 57 (1991) pp. 799–815 |
| [a9] | N. Tzanakis, B.M.M. de Weger, "How to explicitly solve a Thue–Mahler equation" Compositio Math. , 84 (1992) pp. 223–288 |
Thue-Mahler equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Thue-Mahler_equation&oldid=18261