Difference between revisions of "Buchsbaum ring"
(Importing text file) |
m (Automatically changed introduction) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 225 formulas, 223 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|part}} | |
| + | The notion of a Buchsbaum ring (and module) is a generalization of that of a [[Cohen–Macaulay ring|Cohen–Macaulay ring]] (respectively, module). Let $A$ denote a Noetherian [[Local ring|local ring]] (cf. also [[Noetherian ring|Noetherian ring]]) with [[Maximal ideal|maximal ideal]] $\mathfrak{m}$ and $d = \operatorname { dim } A$. Let $M$ be a finitely-generated $A$-module with $\dim_AM = s$. Then $M$ is called a Buchsbaum module if the difference | ||
| − | + | \begin{equation*} \operatorname{l} _ { A } ( M / \mathfrak{q}M ) - e _ { \mathfrak{q} } ^ { 0 } ( M ) \end{equation*} | |
| − | is | + | is independent of the choice of a parameter ideal $\mathfrak { q } = ( a _ { 1 } , \ldots , a _ { s } )$ of $M$, where $a _ { 1 } , \dots , a _ { s }$ is a system of parameters of $M$ and ${\bf l} _ { A } ( M / \text{q}M )$ (respectively, $e _ { \mathfrak{q} } ^ { 0 } ( M )$) denotes the length of the $A$-module $M / \mathfrak { q } M$ (respectively, the multiplicity of $M$ with respect to $\text{q}$). When this is the case, the difference |
| + | |||
| + | \begin{equation*} I ( M ) = {\bf l } _ { A } ( M / \mathfrak { q } M ) - e _ { \mathfrak { q } } ^ { 0 } ( M ) \end{equation*} | ||
| + | |||
| + | is called the Buchsbaum invariant of $M$. The $A$-module $M$ is a Cohen–Macaulay module if and only if $\text{l} _ { A } ( M / \text{q}M ) = e _ { \text{q} } ^ { 0 } ( M )$ for some (and hence for any) parameter ideal $\text{q}$ of $M$, so that $M$ is a Cohen–Macaulay $A$-module if and only if $M$ is a Buchsbaum $A$-module with $I ( M ) = 0$. The ring $A$ is said to be a Buchsbaum ring if $A$ is a Buchsbaum module over itself. If $A$ is a Buchsbaum ring, then $A _ { \mathfrak{p} }$ is a Cohen–Macaulay ring with $\operatorname { dim } A _ { \mathfrak { p } } = \operatorname { dim } A - \operatorname { dim } A / \mathfrak { p }$ for every $\mathfrak{p} \in \operatorname { Spec } A \backslash \{ \mathfrak{m} \}$. | ||
A typical example of Buchsbaum rings is as follows. Let | A typical example of Buchsbaum rings is as follows. Let | ||
| − | + | \begin{equation*} A = B / ( X _ { 1 } , \dots , X _ { d } ) \bigcap ( Y _ { 1 } , \dots , Y _ { d } ), \end{equation*} | |
| − | where | + | where $B = k [ [ X _ { 1 } , \dots , X _ { d } , Y _ { 1 } , \dots , Y _ { d } ]]$, with $d \geq 1$, denotes the [[Formal power series|formal power series]] ring in $2 d$ variables over a [[Field|field]] $k$. Then $A$ is a Buchsbaum ring with $\operatorname { dim } A = d$ and $I ( A ) = d - 1$. |
| − | A, not necessarily local, [[Noetherian ring|Noetherian ring]] | + | A, not necessarily local, [[Noetherian ring|Noetherian ring]] $R$ is said to be a Buchsbaum ring if the local rings $R _ { \mathfrak{p} }$ are Buchsbaum for all $\mathfrak { p } \in \operatorname { Spec } R$. |
| − | The theory of Buchsbaum rings and modules dates back to a question raised in 1965 by D.A. Buchsbaum [[#References|[a3]]]. He asked whether the difference | + | The theory of Buchsbaum rings and modules dates back to a question raised in 1965 by D.A. Buchsbaum [[#References|[a3]]]. He asked whether the difference $ \operatorname{l} _ { A } ( A / \mathfrak { q } ) - e _ { \mathfrak { q } } ^ { 0 } ( A )$, with $\text{q}$ a parameter ideal, is an invariant for any Noetherian local ring $A$. This is, however, not the case and a counterexample was given in [[#References|[a28]]]. Thereafter, in 1973 J. Stückrad and W. Vogel published the classic paper [[#References|[a29]]], from which the history of Buchsbaum rings and modules started. In [[#References|[a29]]] they gave a characterization of Buchsbaum rings in terms of the following property of systems of parameters: A $d$-dimensional Noetherian local ring $A$ with maximal ideal $\mathfrak{m}$ is Buchsbaum if and only if every system $a _ { 1 } , \dots , a _ { d }$ of parameters for $A$ forms a weak $A$-sequence, that is, the equality |
| − | + | \begin{equation*} ( a _ { 1 } , \dots , a _ { i - 1 } ) : a _ { i } = ( a _ { 1 } , \dots , a _ { i - 1 } ) : \mathfrak{m} \end{equation*} | |
| − | holds for all | + | holds for all $1 \leq i \leq d$. Therefore, systems $a _ { 1 } , \dots , a _ { d }$ of parameters in a Buchsbaum local ring need not be regular sequences, but the differences |
| − | + | \begin{equation*} [ ( a _ { 1 } , \dots , a _ { i - 1 } ) : a _ { i } ] / ( a _ { 1 } , \dots , a _ { i - 1 } ) ,\; 1 \leq i \leq d, \end{equation*} | |
| − | are very small and only finite-dimensional vector spaces over the residue class field | + | are very small and only finite-dimensional vector spaces over the residue class field $A /_{ \mathfrak{m}}$ of $A$. Weak sequences are closely related to $d$-sequences introduced by C. Huneke [[#References|[a21]]]. Actually, $A$ is a Buchsbaum ring if and only if every system $a _ { 1 } , \dots , a _ { d }$ of parameters for $A$ forms a $d$-sequence, that is, the equality |
| − | + | \begin{equation*} ( a _ { 1 } , \dots , a _ { i - 1 } ) : a _ { i } a _ { j } = ( a _ { 1 } , \dots , a _ { i - 1 } ) : a _ { j } \end{equation*} | |
| − | holds for all | + | holds for all $1 \leq i \leq j \leq d$. |
One of the fundamental results on Buchsbaum rings and modules is the surjectivity criterion. Let | One of the fundamental results on Buchsbaum rings and modules is the surjectivity criterion. Let | ||
| − | + | \begin{equation*} H _ { \mathfrak{m} } ^ { i } ( M ) = \operatorname { lim } _ { n \rightarrow \infty } \operatorname { Ext } _ { A } ^ { i } ( A / \mathfrak { m } ^ { n } , M ) \quad ( i \in \mathbf{Z} ) \end{equation*} | |
| − | denote the | + | denote the $i$th [[Local cohomology|local cohomology]] of $M$ with respect to the maximal ideal $\mathfrak{m}$. If $M$ is a Buchsbaum $A$-module, then $\mathfrak { m } \cdot H _ { \mathfrak { m } } ^ { i } ( M ) = ( 0 )$ for all $i \neq s$ and the equality |
| − | + | \begin{equation*} \operatorname {I} ( M ) = \sum _ { i = 0 } ^ { s - 1 } \left( \begin{array} { c } { s - 1 } \\ { i } \end{array} \right) .\operatorname { l}_ { A } ( H _ {\frak m } ^ { i } ( M ) ) \end{equation*} | |
| − | holds, where | + | holds, where $s = \operatorname { dim } _ { A } M$. |
| − | Unfortunately, the vanishing does not characterize Buchsbaum modules. Modules | + | Unfortunately, the vanishing does not characterize Buchsbaum modules. Modules $M$ with $\mathfrak { m } \cdot H _ { \mathfrak { m } } ^ { i } ( M ) = ( 0 )$ for all $i \neq \operatorname { dim } _ { A } M$ are called quasi-Buchsbaum and constitute a class which is strictly larger than that of Buchsbaum modules. However, if the canonical homomorphism |
| − | + | \begin{equation*} \varphi _ { M } ^ { i } : \operatorname { Ext } _ { A } ^ { i } ( A / \mathfrak { m } , M ) \rightarrow H _ {\frak m } ^ { i } ( M ) = \operatorname { lim } _ { n \rightarrow \infty } \operatorname { Ext } _ { A } ^ { i } ( A / \mathfrak { m } ^ { n } , M ) \end{equation*} | |
| − | is surjective for all | + | is surjective for all $i \neq \operatorname { dim } _ { A } M$, then $M$ is a Buchsbaum $A$-module. The converse is also true if the base ring $A$ is regular (cf. also [[Regular ring (in commutative algebra)|Regular ring (in commutative algebra)]]). |
| − | After the establishment of the surjectivity criterion, by Stückrad and Vogel [[#References|[a30]]] in 1978, the development of the theory became rather rapid. The ubiquity of Buchsbaum normal local rings was established by S. Goto [[#References|[a6]]] as an application of the Evans–Griffith construction [[#References|[a5]]]. Namely, let | + | After the establishment of the surjectivity criterion, by Stückrad and Vogel [[#References|[a30]]] in 1978, the development of the theory became rather rapid. The ubiquity of Buchsbaum normal local rings was established by S. Goto [[#References|[a6]]] as an application of the Evans–Griffith construction [[#References|[a5]]]. Namely, let $d \geq 1$ and $\{ h _ { i } \} _ { 0 \leq i \leq d - 1 }$ be integers. Then there exists a Buchsbaum local ring $A$ with $\operatorname { dim } A = d$ and $\operatorname{l} _ { A } ( H _ { \text{m} } ^ { i } ( A ) ) = h _ { i }$ for $0 \leq i \leq d - 1$. If $h _ { 0 } = 0$ (respectively, $d \geq 2$ and $h _ { 0 } = h _ { 1 } = 0$), one may choose the ring $A$ so that $A$ is an [[Integral domain|integral domain]] (respectively, a [[Normal ring|normal ring]]). See [[#References|[a1]]] for progress in the research about the ubiquity of Buchsbaum homogeneous integral domains. Besides, Buchsbaum local rings of multiplicity $2$ have been classified [[#References|[a8]]]. Also, certain famous isolated singularities are Buchsbaum (cf. [[#References|[a23]]]). |
| − | The theory of Buchsbaum rings and modules is closely related to that of Cohen–Macaulayness in blowing-ups. Let | + | The theory of Buchsbaum rings and modules is closely related to that of Cohen–Macaulayness in blowing-ups. Let $I$ be an ideal of positive height in a Noetherian local ring $A$. Let $R ( I ) = \oplus _ { n \geq 0 } I ^ { n }$ and call it the Rees algebra of $I$. Then the canonical morphism $\operatorname{Proj} R ( I ) \rightarrow \operatorname{Spec} A$ is the blowing-up of $A$ with centre $I$ (cf. also [[Blow-up algebra|Blow-up algebra]]). If the ring $R ( I )$ is Cohen–Macaulay, then the scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130290/b130290110.png"/> naturally is locally Cohen–Macaulay. The problem when the Rees algebra $R ( I )$ is Cohen–Macaulay has been intensively studied from the 1980s onwards ([[#References|[a18]]], [[#References|[a38]]], [[#References|[a16]]], [[#References|[a39]]], [[#References|[a17]]]). |
| − | The ring | + | The ring $R ( I )$ is Cohen–Macaulay if the ideal $I$ is generated by a regular sequence and if the base ring $A$ is Cohen–Macaulay [[#References|[a2]]]. However, the converse is not true even for parameter ideals $I$. Actually, $A$ is a Buchsbaum ring if and only if the Rees algebra $R ( \mathfrak { q } )$ is a Cohen–Macaulay ring for every parameter ideal $\text{q}$ in $A$, provided that $A$ is an integral domain with $\operatorname { dim } A = 2$. This insightful result of Y. Shimoda [[#References|[a35]]] in 1979 opened the door towards a further development of the theory. Firstly, Goto and Shimoda [[#References|[a19]]] showed that a Noetherian local ring $A$ is a Buchsbaum ring with $H _ { \mathfrak{m} } ^ { i } ( A ) = ( 0 )$ ($i \neq 1 , \operatorname { dim } A$) if and only if the Rees algebra $R ( \mathfrak { q } )$ is a Cohen–Macaulay ring for every parameter ideal $\text{q}$ in $A$. When this is the case, the Rees algebras $R ( \mathfrak{q} ^ { n } )$ are also Cohen–Macaulay for all $n \geq 1$. In 1981, Buchsbaum rings were characterized in terms of the blowing-ups of parameter ideals. Let $A$ be a Noetherian local ring with maximal ideal $\mathfrak{m}$ and $d = \operatorname { dim } A \geq 1$. Then $A / H _ { \mathfrak{m} } ^ { 0 } ( A )$ is a Buchsbaum ring if and only if the scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130290/b130290134.png"/> is locally Cohen–Macaulay for every parameter ideal $\text{q}$ in $A$ [[#References|[a7]]]. Subsequently, Goto [[#References|[a10]]] proved that the associated graded rings $G ( \mathfrak { q } ) = \oplus _ { n \geq 0} \mathfrak { q } ^ { n } / \mathfrak { q } ^ { n + 1 }$ of parameter ideals $\text{q}$ in a Buchsbaum local ring are always Buchsbaum. In addition, Stückrad showed that $R ( \mathfrak { q } )$ is a Buchsbaum ring for every parameter ideal $\text{q}$ in a Buchsbaum local ring [[#References|[a36]]]. The systems of parameters in Buchsbaum local rings behave very well and enjoy the monomial property [[#References|[a10]]]. |
Buchsbaum rings are yet (2000) the only non-trivial case for which the monomial conjecture, raised by M. Hochster, has been solved affirmatively (except for the equi-characteristic case). See [[#References|[a31]]] for these results, together with geometric applications and concrete examples. See [[#References|[a31]]] for researches on the Buchsbaum property in affine semi-group rings and Stanley–Reisner rings of simplicial complexes. | Buchsbaum rings are yet (2000) the only non-trivial case for which the monomial conjecture, raised by M. Hochster, has been solved affirmatively (except for the equi-characteristic case). See [[#References|[a31]]] for these results, together with geometric applications and concrete examples. See [[#References|[a31]]] for researches on the Buchsbaum property in affine semi-group rings and Stanley–Reisner rings of simplicial complexes. | ||
| − | Let | + | Let $M$ be a Buchsbaum module over a Noetherian local ring $A$. Then $M$ is said to be maximal if $\operatorname{dim}_{A} M = \operatorname{dim} A $. Noetherian local rings possessing only finitely many isomorphism classes of indecomposable maximal Buchsbaum modules are said to have finite Buchsbaum-representation type. Buchsbaum representation theory was studied by Goto and K. Nishida [[#References|[a15]]], [[#References|[a11]]], [[#References|[a13]]], and the Cohen–Macaulay local rings $A$ of finite Buchsbaum-representation type have been classified under certain mild conditions. If $\operatorname { dim } A \geq 2$, then $A$ must be regular [[#References|[a15]]]. The situation is a little more complicated if $\operatorname { dim } A = 1$ [[#References|[a13]]]. In [[#References|[a11]]] (not necessarily Cohen–Macaulay) surface singularities of finite Buchsbaum-representation type are classified. |
| − | Suppose that | + | Suppose that $A$ is a regular local ring with $\operatorname { dim } A = d$ and let $M$ be a maximal Buchsbaum $A$-module. Then $M _ { \mathfrak{p} }$ is a free $A _ { \mathfrak{p} }$-module for all $\mathfrak{p} \in \operatorname { Spec } A \backslash \{ \mathfrak{m} \}$, so that the $A$-module $M$ defines a [[Vector bundle|vector bundle]] on the punctured spectrum $\operatorname {Spec} A \backslash \{ \mathfrak{m} \}$ of $A$. Thanks to the surjectivity criterion, one can prove the structure theorem of maximal Buchsbaum modules over regular local rings: Every maximal Buchsbaum $A$-module $M$ has the form |
| − | + | \begin{equation*} M \cong \bigoplus _ { i = 0 } ^ { d } E _ { i } ^ { h _ { i } }, \end{equation*} | |
| − | where | + | where $E_i$ denotes the $i$th syzygy module of the residue class field $A /_{ \mathfrak{m}}$ of $A$, $h _ { i } = \operatorname { l } _ { A } ( H _ { \mathfrak{m} } ^ { i } ( M ) )$ ($0 \leq i \leq d - 1$), and $h _ { d } = \operatorname { rank } _ { A } M - \sum _ { i = 1 } ^ { d - 1 } \left( \begin{array} { c } { d - 1 } \\ { i - 1 } \end{array} \right) h _ { i }$, if $A$ is a regular local ring ([[#References|[a4]]], [[#References|[a12]]]). This result has been generalized by Y. Yoshino [[#References|[a40]]] and T. Kawasaki [[#References|[a24]]]. They showed a similar decomposition theorem of a special kind of maximal Buchsbaum modules over Gorenstein local rings; see [[#References|[a32]]] for the characterization of Buchsbaum rings and modules in terms of dualizing complexes. (It should be noted here that the main result in [[#References|[a32]]] contains a serious mistake, which has been repaired in [[#References|[a40]]].) |
| − | A local ring | + | A local ring $A$ satisfying the condition that all the local cohomology modules $H _ { \mathfrak{m} } ^ { i } ( A )$ ($i \neq \operatorname { dim } A$) are finitely generated is said to be an FLC ring (or a generalized Cohen–Macaulay ring). The class of FLC rings includes Buchsbaum rings as typical examples. In fact, a Noetherian local ring $A$ is FLC if and only if it contains at least one system $a _ { 1 } , \dots , a _ { d }$ ($d = \operatorname { dim } A$) of parameters such that the sequence $\alpha _ { 1 } ^ { n _ { 1 } } , \dots , \alpha _ { d } ^ { n _ { d } }$ forms a $d$-sequence in any order for all integers $n _ { i } \geq 1$. Such a sequence is called an unconditioned strong $d$-sequence (for short, USD-sequence or $d ^ { + }$-sequence); they have been intensively studied [[#References|[a27]]], [[#References|[a37]]], [[#References|[a20]]]. Recently (1999), Kawasaki [[#References|[a25]]] used the results in [[#References|[a20]]] to establish the arithmetic Cohen–Macaulayfications of Noetherian local rings. Namely, every unmixed local ring $A$ contains an ideal $I$ of positive height with the Cohen–Macaulay Rees algebra $R ( I )$, provided $\operatorname { dim } A \geq 1$ and all the formal fibres of $A$ are Cohen–Macaulay. Hence, the Sharp conjecture [[#References|[a34]]] concerning the existence of dualizing complexes is solved affirmatively. |
| − | Let | + | Let $R = \oplus _ { n \geq 0} R _ { n }$ be a Noetherian graded ring with $k = R _ { 0 }$ a field and let $\mathfrak { M } = R _ { + }$. Then $R$ is a Buchsbaum ring if and only if the local ring $R _ {\frak M }$ is Buchsbaum. When this is the case, the local cohomology modules $H _ { \mathfrak{M} } ^ { i } ( R )$ ($i \neq \operatorname { dim } R$) are finite-dimensional vector spaces over the field $k$. The vanishing of certain homogeneous components $[ H _ { \mathfrak{M} } ^ { i } ( R ) ] _ { n }$ of $H _ { \mathfrak{M} } ^ { i } ( R )$ may affect the Buchsbaumness in graded algebras $R$. For example, if there exist integers $\{ t _ { i } \} _ { 0 \leq i \leq d - 1}$ ($d = \operatorname { dim } R$) such that $t _ { i } \leq t_{i + 1} + 1$ for all $0 \leq i \leq d - 1$ and if |
| − | + | \begin{equation*} [ H _ { \mathfrak{M} } ^ { i } ( R ) ] _ { n } = ( 0 ) \end{equation*} | |
| − | for all | + | for all $n \neq t_i$ and $0 \leq i \leq d - 1$, then $R$ is a Buchsbaum ring [[#References|[a9]]]. Therefore $R$ is a Buchsbaum ring if $H _ { \mathfrak{M} } ^ { i } ( R ) = [ H _ { \mathfrak{M} } ^ { i } ( R ) ] _ { 0 }$ for all $i \neq d$ [[#References|[a33]]]. Hence the scheme $X = \operatorname { Proj } R$ is arithmetically Buchsbaum if $X$ is locally Cohen–Macaulay, provided that $R = k [ R _ { 1 }]$ and $R$ is equi-dimensional. See [[#References|[a22]]] for the bounds of Castelnuovo–Mumford regularities of Buchsbaum schemes $X = \operatorname { Proj } R$. |
| − | Researches of the Buchsbaumness in Rees algebras recently (1999) started again, although the progress remains tardy (possibly because of the lack of characterizations of Trung–Ikeda type [[#References|[a38]]] for Buchsbaumness). In [[#References|[a14]]] the Buchsbaumness in Rees algebras | + | Researches of the Buchsbaumness in Rees algebras recently (1999) started again, although the progress remains tardy (possibly because of the lack of characterizations of Trung–Ikeda type [[#References|[a38]]] for Buchsbaumness). In [[#References|[a14]]] the Buchsbaumness in Rees algebras $R ( I )$ of certain $\mathfrak{m}$-primary ideals $I$ in Cohen–Macaulay local rings is closely studied in connection with the Buchsbaumness in the associated graded rings $G ( I ) = \oplus _ { n \geq 0} I ^ { n } / I ^ { n + 1 }$ and that of the extended Rees algebras $R ^ { \prime } ( I ) = \oplus _ { n \in \bf Z} I^ { n }$. In [[#References|[a26]]], [[#References|[a41]]], [[#References|[a42]]], Buchsbaumness in graded rings associated to certain $\mathfrak{m}$-primary ideals in Buchsbaum local rings is explored. Especially, the Rees algebra $R ( \mathfrak{m} )$ of the maximal ideal $\mathfrak{m}$ in a Buchsbaum local ring $A$ of maximal embedding dimension (that is, a Buchsbaum local ring $A$ for which the equality $v ( A ) = e _ { \mathfrak{m} } ^ { 0 } ( A ) + \operatorname { dim } A + I ( A ) - 1$ holds) is again a Buchsbaum ring [[#References|[a42]]]. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> M. Amasaki, "Existence of homogeneous prime ideals fitting into long Bourbaki sequences" , ''Proc. 21st Symp. Commutative Algebra in Tokyo, Japan, November 23-26, 1999'' (1999) pp. 104–111 {{MR|1610925}} {{ZBL|}} </td></tr><tr><td valign="top">[a2]</td> <td valign="top"> J. Barshay, "Graded algebras of powers of ideals generated by A-sequences" ''J. Algebra'' , '''25''' (1973) pp. 90–99 {{MR|0332748}} {{ZBL|0256.13017}} </td></tr><tr><td valign="top">[a3]</td> <td valign="top"> D.A. Buchsbaum, "Complexes in local ring theory" , ''Some Aspects of Ring Theory'' , C.I.M.E. Roma (1965) pp. 223–228 {{MR|}} {{ZBL|0178.37201}} </td></tr><tr><td valign="top">[a4]</td> <td valign="top"> G. Eisenbud, S. Goto, "Linear free resolutions and minimal multiplicity" ''J. Algebra'' , '''88''' (1984) pp. 89–133 {{MR|0741934}} {{ZBL|0531.13015}} </td></tr><tr><td valign="top">[a5]</td> <td valign="top"> E.G. Evans Jr., P.A. Griffith, "Local cohomology modules for normal domains" ''J. London Math. Soc.'' , '''19''' (1979) pp. 277–284 {{MR|0533326}} {{ZBL|0407.13019}} </td></tr><tr><td valign="top">[a6]</td> <td valign="top"> S. Goto, "On Buchsbaum rings" ''J. Algebra'' , '''67''' (1980) pp. 272–279 {{MR|0602063}} {{ZBL|0473.13010}} {{ZBL|0473.13009}} {{ZBL|0413.13012}} </td></tr><tr><td valign="top">[a7]</td> <td valign="top"> S. Goto, "Blowing-up of Buchsbaum rings" , ''Commutative Algebra'' , ''Lecture Notes'' , '''72''' , London Math. Soc. (1981) pp. 140–162 {{MR|0693633}} {{ZBL|0519.13021}} </td></tr><tr><td valign="top">[a8]</td> <td valign="top"> S. Goto, "Buchsbaum rings with multiplicity 2" ''J. Algebra'' , '''74''' (1982) pp. 494–508 {{MR|0647250}} {{ZBL|0479.13007}} </td></tr><tr><td valign="top">[a9]</td> <td valign="top"> S. Goto, "Buchsbaum rings of maximal embedding dimension" ''J. Algebra'' , '''76''' (1982) pp. 383–399 {{MR|0661862}} {{ZBL|0482.13012}} </td></tr><tr><td valign="top">[a10]</td> <td valign="top"> S. Goto, "On the associated graded rings of parameter ideals in Buchsbaum rings" ''J. Algebra'' , '''85''' (1983) pp. 490–534 {{MR|0725097}} {{ZBL|0529.13010}} </td></tr><tr><td valign="top">[a11]</td> <td valign="top"> S. Goto, "Surface singularities of finite Buchsbaum-representation type" , ''Commutative Algebra: Proc. Microprogram June 15–July 2'' , Springer (1987) pp. 247–263 {{MR|1015521}} {{ZBL|0741.13015}} </td></tr><tr><td valign="top">[a12]</td> <td valign="top"> S. Goto, "Maximal Buchsbaum modules over regular local rings and a structure theorem for generalized Cohen–Macaulay modules" M. Nagata (ed.) H. Matsumura (ed.) , ''Commutative Algebra and Combinatorics'' , ''Adv. Stud. Pure Math.'' , '''11''' , Kinokuniya (1987) pp. 39–46 {{MR|0951196}} {{ZBL|0649.13009}} </td></tr><tr><td valign="top">[a13]</td> <td valign="top"> S. Goto, "Curve singularities of finite Buchsbaum-representation type" ''J. Algebra'' , '''163''' (1994) pp. 447–480 {{MR|1262714}} {{ZBL|0807.13007}} </td></tr><tr><td valign="top">[a14]</td> <td valign="top"> S. Goto, "Buchsbaumness in Rees algebras associated to ideals of minimal multiplicity" ''J. Algebra'' , '''213''' (1999) pp. 604–661 {{MR|1673472}} {{ZBL|0942.13003}} </td></tr><tr><td valign="top">[a15]</td> <td valign="top"> S. Goto, K. Nishida, "Rings with only finitely many isomorphism classes of indecomposable maximal Buchsbaum modules" ''J. Math. Soc. Japan'' , '''40''' (1988) pp. 501–518 {{MR|0945349}} {{ZBL|0657.13022}} </td></tr><tr><td valign="top">[a16]</td> <td valign="top"> S. Goto, K. Nishida, "The Cohen–Macaulay and Gorenstein Rees algebras associated to filtrations" , ''Memoirs'' , '''526''' , Amer. Math. Soc. (1994) {{MR|1287443}} {{ZBL|0812.13016}} </td></tr><tr><td valign="top">[a17]</td> <td valign="top"> S. Goto, Y. Nakamura, K. Nishida, "Cohen–Macaulay graded rings associated ideals" ''Amer. J. Math.'' , '''118''' (1996) pp. 1197–1213 {{MR|}} {{ZBL|0878.13002}} </td></tr><tr><td valign="top">[a18]</td> <td valign="top"> S. Goto, Y. Shimoda, "On the Rees algebras of Cohen–Macaulay local rings" R.N. Draper (ed.) , ''Commutative Algebra, Analytic Methods'' , ''Lecture Notes in Pure Applied Math.'' , '''68''' , M. Dekker (1982) pp. 201–231 {{MR|0655805}} {{ZBL|0482.13011}} </td></tr><tr><td valign="top">[a19]</td> <td valign="top"> S. Goto, Y. Shimoda, "On Rees algebras over Buchsbaum rings" ''J. Math. Kyoto Univ.'' , '''20''' (1980) pp. 691–708 {{MR|0592354}} {{ZBL|0473.13010}} </td></tr><tr><td valign="top">[a20]</td> <td valign="top"> S. Goto, K. Yamagishi, "The theory of unconditioned strong $d$-sequences and modules of finite local cohomology" ''Preprint'' (1978)</td></tr><tr><td valign="top">[a21]</td> <td valign="top"> C. Huneke, "The theory of d-sequences and powers of ideals" ''Adv. Math.'' , '''46''' (1982) pp. 249–279 {{MR|0683201}} {{ZBL|0505.13004}} </td></tr><tr><td valign="top">[a22]</td> <td valign="top"> L.T. Hoa, C. Miyazaki, "Bounds on Castelnuovo–Mumford regularity for generalized Cohen–Macaulay graded rings" ''Math. Ann.'' , '''301''' (1995) pp. 587–598 {{MR|1324528}} {{ZBL|0834.13016}} </td></tr><tr><td valign="top">[a23]</td> <td valign="top"> M.-N. Ishida, "Tsuchihashi's cusp singularities are Buchsbaum singularities" ''Tôhoku Math. J.'' , '''36''' (1984) pp. 191–201 {{MR|742594}} {{ZBL|}} </td></tr><tr><td valign="top">[a24]</td> <td valign="top"> T. Kawasaki, "Local cohomology modules of indecomposable surjective–Buchsbaum modules over Gorenstein local rings" ''J. Math. Soc. Japan'' , '''48''' (1996) pp. 551–566 {{MR|1389995}} {{ZBL|0866.13007}} </td></tr><tr><td valign="top">[a25]</td> <td valign="top"> T. Kawasaki, "Arithmetic Cohen–Macaulayfications of local rings" , ''Proc. 21st Symp. Commutative Algebra in Tokyo, Japan, November 23-26, 1999'' (1999) pp. 88–92</td></tr><tr><td valign="top">[a26]</td> <td valign="top"> Y. Nakamura, "On the Buchsbaum property of associated graded rings" ''J. Algebra'' , '''209''' (1998) pp. 345–366 {{MR|1652142}} {{ZBL|0942.13002}} </td></tr><tr><td valign="top">[a27]</td> <td valign="top"> P. Schenzel, N.V. Trung, N.T. Cuong, "Verallgemeinerte Cohen–Macaulay-Moduln" ''Math. Nachr.'' , '''85''' (1978) pp. 57–73 {{MR|0517641}} {{ZBL|0398.13014}} </td></tr><tr><td valign="top">[a28]</td> <td valign="top"> J. Stückrad, W. Vogel, "Ein Korrekturglied in der Multiplizitätstheorie von D.G. Northcott und Anwendungen" ''Monatsh. Math.'' , '''76''' (1972) pp. 264–271 {{MR|}} {{ZBL|0248.13026}} </td></tr><tr><td valign="top">[a29]</td> <td valign="top"> J. Stückrad, W. Vogel, "Eine Verallgemeinerung der Cohen–Macaulay-Ringe und Anwendungen auf ein Problem der Multiplitätstheorie" ''J. Math. Kyoto Univ.'' , '''13''' (1973) pp. 513–528</td></tr><tr><td valign="top">[a30]</td> <td valign="top"> J. Stückrad, W. Vogel, "Toward a theory of Buchsbaum singularities" ''Amer. J. Math.'' , '''100''' (1978) pp. 727–746 {{MR|0509072}} {{ZBL|0429.14001}} </td></tr><tr><td valign="top">[a31]</td> <td valign="top"> J. Stückrad, W. Vogel, "Buchsbaum rings and applications" , Springer (1986) {{MR|0881220}} {{MR|0873945}} {{ZBL|0606.13018}} {{ZBL|0606.13017}} </td></tr><tr><td valign="top">[a32]</td> <td valign="top"> P. Schenzel, "Dualisierende Komplexe in der lokalen Algebra und Buchsbaum–Ringe" , ''Lecture Notes in Mathematics'' , '''907''' , Springer (1982) {{MR|0654151}} {{ZBL|0484.13016}} </td></tr><tr><td valign="top">[a33]</td> <td valign="top"> P. Schenzel, "On Veronesean embeddings and projections of Veronesean varieties" ''Archiv Math.'' , '''30''' (1978) pp. 391–397 {{MR|0485849}} {{ZBL|0417.14040}} </td></tr><tr><td valign="top">[a34]</td> <td valign="top"> R.Y. Sharp, "Necessary conditions for the existence of dualizing complexes in commutative algebra" , ''Lecture Notes in Mathematics'' , '''740''' , Springer (1979) pp. 213–229 {{MR|0563505}} {{ZBL|0421.13003}} </td></tr><tr><td valign="top">[a35]</td> <td valign="top"> Y. Shimoda, "A note on Rees algebras of two-dimensional local domains" ''J. Math. Kyoto Univ.'' , '''19''' (1979) pp. 327–333 {{MR|0545713}} {{ZBL|0447.13010}} </td></tr><tr><td valign="top">[a36]</td> <td valign="top"> J. Stückrad, "On the Buchsbaum property of Rees and form modules" ''Beitr. Algebra Geom.'' , '''19''' (1985) pp. 83–103 {{MR|0785248}} {{ZBL|0567.13008}} </td></tr><tr><td valign="top">[a37]</td> <td valign="top"> N.V. Trung, "Toward a theory of generalized Cohen–Macaulay modules" ''Nagoya Math. J.'' , '''102''' (1986) pp. 1–49 {{MR|}} {{ZBL|0649.13008}} {{ZBL|0637.13013}} </td></tr><tr><td valign="top">[a38]</td> <td valign="top"> N.V. Trung, S. Ikeda, "When is the Rees algebra Cohen–Macaulay?" ''Commun. Algebra'' , '''17''' (1989) pp. 2893–2922 {{MR|}} {{ZBL|0696.13015}} </td></tr><tr><td valign="top">[a39]</td> <td valign="top"> W. Vasconcelos, "Arithmetic of blowup algebras" , ''London Math. Soc. Lecture Notes'' , '''195''' , Cambridge Univ. Press (1994) {{MR|1275840}} {{ZBL|0813.13008}} </td></tr><tr><td valign="top">[a40]</td> <td valign="top"> Y. Yoshino, "Maximal Buchsbaum modules of finite projective dimension" ''J. Algebra'' , '''159''' (1993) pp. 240–264 {{MR|1231212}} {{ZBL|0791.13009}} </td></tr><tr><td valign="top">[a41]</td> <td valign="top"> K. Yamagishi, "The associated graded modules of Buchsbaum modules with respect to $\mathfrak{m}$-primary ideals in equi-I-invariant case" ''J. Algebra'' , '''225''' (2000) pp. 1–27 {{MR|1743648}} {{ZBL|}} </td></tr><tr><td valign="top">[a42]</td> <td valign="top"> K. Yamagishi, "Buchsbaumness in Rees algebras associated to $\mathfrak{m}$-primary ideals of minimal multiplicity in Buchsbaum local rings" , ''Proc. 21st Symp. Commutative Algebra in Tokyo, Japan, November 23-26, 1999'' (1999) pp. 39–45</td></tr></table> |
Latest revision as of 17:43, 1 July 2020
The notion of a Buchsbaum ring (and module) is a generalization of that of a Cohen–Macaulay ring (respectively, module). Let $A$ denote a Noetherian local ring (cf. also Noetherian ring) with maximal ideal $\mathfrak{m}$ and $d = \operatorname { dim } A$. Let $M$ be a finitely-generated $A$-module with $\dim_AM = s$. Then $M$ is called a Buchsbaum module if the difference
\begin{equation*} \operatorname{l} _ { A } ( M / \mathfrak{q}M ) - e _ { \mathfrak{q} } ^ { 0 } ( M ) \end{equation*}
is independent of the choice of a parameter ideal $\mathfrak { q } = ( a _ { 1 } , \ldots , a _ { s } )$ of $M$, where $a _ { 1 } , \dots , a _ { s }$ is a system of parameters of $M$ and ${\bf l} _ { A } ( M / \text{q}M )$ (respectively, $e _ { \mathfrak{q} } ^ { 0 } ( M )$) denotes the length of the $A$-module $M / \mathfrak { q } M$ (respectively, the multiplicity of $M$ with respect to $\text{q}$). When this is the case, the difference
\begin{equation*} I ( M ) = {\bf l } _ { A } ( M / \mathfrak { q } M ) - e _ { \mathfrak { q } } ^ { 0 } ( M ) \end{equation*}
is called the Buchsbaum invariant of $M$. The $A$-module $M$ is a Cohen–Macaulay module if and only if $\text{l} _ { A } ( M / \text{q}M ) = e _ { \text{q} } ^ { 0 } ( M )$ for some (and hence for any) parameter ideal $\text{q}$ of $M$, so that $M$ is a Cohen–Macaulay $A$-module if and only if $M$ is a Buchsbaum $A$-module with $I ( M ) = 0$. The ring $A$ is said to be a Buchsbaum ring if $A$ is a Buchsbaum module over itself. If $A$ is a Buchsbaum ring, then $A _ { \mathfrak{p} }$ is a Cohen–Macaulay ring with $\operatorname { dim } A _ { \mathfrak { p } } = \operatorname { dim } A - \operatorname { dim } A / \mathfrak { p }$ for every $\mathfrak{p} \in \operatorname { Spec } A \backslash \{ \mathfrak{m} \}$.
A typical example of Buchsbaum rings is as follows. Let
\begin{equation*} A = B / ( X _ { 1 } , \dots , X _ { d } ) \bigcap ( Y _ { 1 } , \dots , Y _ { d } ), \end{equation*}
where $B = k [ [ X _ { 1 } , \dots , X _ { d } , Y _ { 1 } , \dots , Y _ { d } ]]$, with $d \geq 1$, denotes the formal power series ring in $2 d$ variables over a field $k$. Then $A$ is a Buchsbaum ring with $\operatorname { dim } A = d$ and $I ( A ) = d - 1$.
A, not necessarily local, Noetherian ring $R$ is said to be a Buchsbaum ring if the local rings $R _ { \mathfrak{p} }$ are Buchsbaum for all $\mathfrak { p } \in \operatorname { Spec } R$.
The theory of Buchsbaum rings and modules dates back to a question raised in 1965 by D.A. Buchsbaum [a3]. He asked whether the difference $ \operatorname{l} _ { A } ( A / \mathfrak { q } ) - e _ { \mathfrak { q } } ^ { 0 } ( A )$, with $\text{q}$ a parameter ideal, is an invariant for any Noetherian local ring $A$. This is, however, not the case and a counterexample was given in [a28]. Thereafter, in 1973 J. Stückrad and W. Vogel published the classic paper [a29], from which the history of Buchsbaum rings and modules started. In [a29] they gave a characterization of Buchsbaum rings in terms of the following property of systems of parameters: A $d$-dimensional Noetherian local ring $A$ with maximal ideal $\mathfrak{m}$ is Buchsbaum if and only if every system $a _ { 1 } , \dots , a _ { d }$ of parameters for $A$ forms a weak $A$-sequence, that is, the equality
\begin{equation*} ( a _ { 1 } , \dots , a _ { i - 1 } ) : a _ { i } = ( a _ { 1 } , \dots , a _ { i - 1 } ) : \mathfrak{m} \end{equation*}
holds for all $1 \leq i \leq d$. Therefore, systems $a _ { 1 } , \dots , a _ { d }$ of parameters in a Buchsbaum local ring need not be regular sequences, but the differences
\begin{equation*} [ ( a _ { 1 } , \dots , a _ { i - 1 } ) : a _ { i } ] / ( a _ { 1 } , \dots , a _ { i - 1 } ) ,\; 1 \leq i \leq d, \end{equation*}
are very small and only finite-dimensional vector spaces over the residue class field $A /_{ \mathfrak{m}}$ of $A$. Weak sequences are closely related to $d$-sequences introduced by C. Huneke [a21]. Actually, $A$ is a Buchsbaum ring if and only if every system $a _ { 1 } , \dots , a _ { d }$ of parameters for $A$ forms a $d$-sequence, that is, the equality
\begin{equation*} ( a _ { 1 } , \dots , a _ { i - 1 } ) : a _ { i } a _ { j } = ( a _ { 1 } , \dots , a _ { i - 1 } ) : a _ { j } \end{equation*}
holds for all $1 \leq i \leq j \leq d$.
One of the fundamental results on Buchsbaum rings and modules is the surjectivity criterion. Let
\begin{equation*} H _ { \mathfrak{m} } ^ { i } ( M ) = \operatorname { lim } _ { n \rightarrow \infty } \operatorname { Ext } _ { A } ^ { i } ( A / \mathfrak { m } ^ { n } , M ) \quad ( i \in \mathbf{Z} ) \end{equation*}
denote the $i$th local cohomology of $M$ with respect to the maximal ideal $\mathfrak{m}$. If $M$ is a Buchsbaum $A$-module, then $\mathfrak { m } \cdot H _ { \mathfrak { m } } ^ { i } ( M ) = ( 0 )$ for all $i \neq s$ and the equality
\begin{equation*} \operatorname {I} ( M ) = \sum _ { i = 0 } ^ { s - 1 } \left( \begin{array} { c } { s - 1 } \\ { i } \end{array} \right) .\operatorname { l}_ { A } ( H _ {\frak m } ^ { i } ( M ) ) \end{equation*}
holds, where $s = \operatorname { dim } _ { A } M$.
Unfortunately, the vanishing does not characterize Buchsbaum modules. Modules $M$ with $\mathfrak { m } \cdot H _ { \mathfrak { m } } ^ { i } ( M ) = ( 0 )$ for all $i \neq \operatorname { dim } _ { A } M$ are called quasi-Buchsbaum and constitute a class which is strictly larger than that of Buchsbaum modules. However, if the canonical homomorphism
\begin{equation*} \varphi _ { M } ^ { i } : \operatorname { Ext } _ { A } ^ { i } ( A / \mathfrak { m } , M ) \rightarrow H _ {\frak m } ^ { i } ( M ) = \operatorname { lim } _ { n \rightarrow \infty } \operatorname { Ext } _ { A } ^ { i } ( A / \mathfrak { m } ^ { n } , M ) \end{equation*}
is surjective for all $i \neq \operatorname { dim } _ { A } M$, then $M$ is a Buchsbaum $A$-module. The converse is also true if the base ring $A$ is regular (cf. also Regular ring (in commutative algebra)).
After the establishment of the surjectivity criterion, by Stückrad and Vogel [a30] in 1978, the development of the theory became rather rapid. The ubiquity of Buchsbaum normal local rings was established by S. Goto [a6] as an application of the Evans–Griffith construction [a5]. Namely, let $d \geq 1$ and $\{ h _ { i } \} _ { 0 \leq i \leq d - 1 }$ be integers. Then there exists a Buchsbaum local ring $A$ with $\operatorname { dim } A = d$ and $\operatorname{l} _ { A } ( H _ { \text{m} } ^ { i } ( A ) ) = h _ { i }$ for $0 \leq i \leq d - 1$. If $h _ { 0 } = 0$ (respectively, $d \geq 2$ and $h _ { 0 } = h _ { 1 } = 0$), one may choose the ring $A$ so that $A$ is an integral domain (respectively, a normal ring). See [a1] for progress in the research about the ubiquity of Buchsbaum homogeneous integral domains. Besides, Buchsbaum local rings of multiplicity $2$ have been classified [a8]. Also, certain famous isolated singularities are Buchsbaum (cf. [a23]).
The theory of Buchsbaum rings and modules is closely related to that of Cohen–Macaulayness in blowing-ups. Let $I$ be an ideal of positive height in a Noetherian local ring $A$. Let $R ( I ) = \oplus _ { n \geq 0 } I ^ { n }$ and call it the Rees algebra of $I$. Then the canonical morphism $\operatorname{Proj} R ( I ) \rightarrow \operatorname{Spec} A$ is the blowing-up of $A$ with centre $I$ (cf. also Blow-up algebra). If the ring $R ( I )$ is Cohen–Macaulay, then the scheme 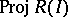 naturally is locally Cohen–Macaulay. The problem when the Rees algebra $R ( I )$ is Cohen–Macaulay has been intensively studied from the 1980s onwards ([a18], [a38], [a16], [a39], [a17]).
naturally is locally Cohen–Macaulay. The problem when the Rees algebra $R ( I )$ is Cohen–Macaulay has been intensively studied from the 1980s onwards ([a18], [a38], [a16], [a39], [a17]).
The ring $R ( I )$ is Cohen–Macaulay if the ideal $I$ is generated by a regular sequence and if the base ring $A$ is Cohen–Macaulay [a2]. However, the converse is not true even for parameter ideals $I$. Actually, $A$ is a Buchsbaum ring if and only if the Rees algebra $R ( \mathfrak { q } )$ is a Cohen–Macaulay ring for every parameter ideal $\text{q}$ in $A$, provided that $A$ is an integral domain with $\operatorname { dim } A = 2$. This insightful result of Y. Shimoda [a35] in 1979 opened the door towards a further development of the theory. Firstly, Goto and Shimoda [a19] showed that a Noetherian local ring $A$ is a Buchsbaum ring with $H _ { \mathfrak{m} } ^ { i } ( A ) = ( 0 )$ ($i \neq 1 , \operatorname { dim } A$) if and only if the Rees algebra $R ( \mathfrak { q } )$ is a Cohen–Macaulay ring for every parameter ideal $\text{q}$ in $A$. When this is the case, the Rees algebras $R ( \mathfrak{q} ^ { n } )$ are also Cohen–Macaulay for all $n \geq 1$. In 1981, Buchsbaum rings were characterized in terms of the blowing-ups of parameter ideals. Let $A$ be a Noetherian local ring with maximal ideal $\mathfrak{m}$ and $d = \operatorname { dim } A \geq 1$. Then $A / H _ { \mathfrak{m} } ^ { 0 } ( A )$ is a Buchsbaum ring if and only if the scheme 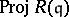 is locally Cohen–Macaulay for every parameter ideal $\text{q}$ in $A$ [a7]. Subsequently, Goto [a10] proved that the associated graded rings $G ( \mathfrak { q } ) = \oplus _ { n \geq 0} \mathfrak { q } ^ { n } / \mathfrak { q } ^ { n + 1 }$ of parameter ideals $\text{q}$ in a Buchsbaum local ring are always Buchsbaum. In addition, Stückrad showed that $R ( \mathfrak { q } )$ is a Buchsbaum ring for every parameter ideal $\text{q}$ in a Buchsbaum local ring [a36]. The systems of parameters in Buchsbaum local rings behave very well and enjoy the monomial property [a10].
is locally Cohen–Macaulay for every parameter ideal $\text{q}$ in $A$ [a7]. Subsequently, Goto [a10] proved that the associated graded rings $G ( \mathfrak { q } ) = \oplus _ { n \geq 0} \mathfrak { q } ^ { n } / \mathfrak { q } ^ { n + 1 }$ of parameter ideals $\text{q}$ in a Buchsbaum local ring are always Buchsbaum. In addition, Stückrad showed that $R ( \mathfrak { q } )$ is a Buchsbaum ring for every parameter ideal $\text{q}$ in a Buchsbaum local ring [a36]. The systems of parameters in Buchsbaum local rings behave very well and enjoy the monomial property [a10].
Buchsbaum rings are yet (2000) the only non-trivial case for which the monomial conjecture, raised by M. Hochster, has been solved affirmatively (except for the equi-characteristic case). See [a31] for these results, together with geometric applications and concrete examples. See [a31] for researches on the Buchsbaum property in affine semi-group rings and Stanley–Reisner rings of simplicial complexes.
Let $M$ be a Buchsbaum module over a Noetherian local ring $A$. Then $M$ is said to be maximal if $\operatorname{dim}_{A} M = \operatorname{dim} A $. Noetherian local rings possessing only finitely many isomorphism classes of indecomposable maximal Buchsbaum modules are said to have finite Buchsbaum-representation type. Buchsbaum representation theory was studied by Goto and K. Nishida [a15], [a11], [a13], and the Cohen–Macaulay local rings $A$ of finite Buchsbaum-representation type have been classified under certain mild conditions. If $\operatorname { dim } A \geq 2$, then $A$ must be regular [a15]. The situation is a little more complicated if $\operatorname { dim } A = 1$ [a13]. In [a11] (not necessarily Cohen–Macaulay) surface singularities of finite Buchsbaum-representation type are classified.
Suppose that $A$ is a regular local ring with $\operatorname { dim } A = d$ and let $M$ be a maximal Buchsbaum $A$-module. Then $M _ { \mathfrak{p} }$ is a free $A _ { \mathfrak{p} }$-module for all $\mathfrak{p} \in \operatorname { Spec } A \backslash \{ \mathfrak{m} \}$, so that the $A$-module $M$ defines a vector bundle on the punctured spectrum $\operatorname {Spec} A \backslash \{ \mathfrak{m} \}$ of $A$. Thanks to the surjectivity criterion, one can prove the structure theorem of maximal Buchsbaum modules over regular local rings: Every maximal Buchsbaum $A$-module $M$ has the form
\begin{equation*} M \cong \bigoplus _ { i = 0 } ^ { d } E _ { i } ^ { h _ { i } }, \end{equation*}
where $E_i$ denotes the $i$th syzygy module of the residue class field $A /_{ \mathfrak{m}}$ of $A$, $h _ { i } = \operatorname { l } _ { A } ( H _ { \mathfrak{m} } ^ { i } ( M ) )$ ($0 \leq i \leq d - 1$), and $h _ { d } = \operatorname { rank } _ { A } M - \sum _ { i = 1 } ^ { d - 1 } \left( \begin{array} { c } { d - 1 } \\ { i - 1 } \end{array} \right) h _ { i }$, if $A$ is a regular local ring ([a4], [a12]). This result has been generalized by Y. Yoshino [a40] and T. Kawasaki [a24]. They showed a similar decomposition theorem of a special kind of maximal Buchsbaum modules over Gorenstein local rings; see [a32] for the characterization of Buchsbaum rings and modules in terms of dualizing complexes. (It should be noted here that the main result in [a32] contains a serious mistake, which has been repaired in [a40].)
A local ring $A$ satisfying the condition that all the local cohomology modules $H _ { \mathfrak{m} } ^ { i } ( A )$ ($i \neq \operatorname { dim } A$) are finitely generated is said to be an FLC ring (or a generalized Cohen–Macaulay ring). The class of FLC rings includes Buchsbaum rings as typical examples. In fact, a Noetherian local ring $A$ is FLC if and only if it contains at least one system $a _ { 1 } , \dots , a _ { d }$ ($d = \operatorname { dim } A$) of parameters such that the sequence $\alpha _ { 1 } ^ { n _ { 1 } } , \dots , \alpha _ { d } ^ { n _ { d } }$ forms a $d$-sequence in any order for all integers $n _ { i } \geq 1$. Such a sequence is called an unconditioned strong $d$-sequence (for short, USD-sequence or $d ^ { + }$-sequence); they have been intensively studied [a27], [a37], [a20]. Recently (1999), Kawasaki [a25] used the results in [a20] to establish the arithmetic Cohen–Macaulayfications of Noetherian local rings. Namely, every unmixed local ring $A$ contains an ideal $I$ of positive height with the Cohen–Macaulay Rees algebra $R ( I )$, provided $\operatorname { dim } A \geq 1$ and all the formal fibres of $A$ are Cohen–Macaulay. Hence, the Sharp conjecture [a34] concerning the existence of dualizing complexes is solved affirmatively.
Let $R = \oplus _ { n \geq 0} R _ { n }$ be a Noetherian graded ring with $k = R _ { 0 }$ a field and let $\mathfrak { M } = R _ { + }$. Then $R$ is a Buchsbaum ring if and only if the local ring $R _ {\frak M }$ is Buchsbaum. When this is the case, the local cohomology modules $H _ { \mathfrak{M} } ^ { i } ( R )$ ($i \neq \operatorname { dim } R$) are finite-dimensional vector spaces over the field $k$. The vanishing of certain homogeneous components $[ H _ { \mathfrak{M} } ^ { i } ( R ) ] _ { n }$ of $H _ { \mathfrak{M} } ^ { i } ( R )$ may affect the Buchsbaumness in graded algebras $R$. For example, if there exist integers $\{ t _ { i } \} _ { 0 \leq i \leq d - 1}$ ($d = \operatorname { dim } R$) such that $t _ { i } \leq t_{i + 1} + 1$ for all $0 \leq i \leq d - 1$ and if
\begin{equation*} [ H _ { \mathfrak{M} } ^ { i } ( R ) ] _ { n } = ( 0 ) \end{equation*}
for all $n \neq t_i$ and $0 \leq i \leq d - 1$, then $R$ is a Buchsbaum ring [a9]. Therefore $R$ is a Buchsbaum ring if $H _ { \mathfrak{M} } ^ { i } ( R ) = [ H _ { \mathfrak{M} } ^ { i } ( R ) ] _ { 0 }$ for all $i \neq d$ [a33]. Hence the scheme $X = \operatorname { Proj } R$ is arithmetically Buchsbaum if $X$ is locally Cohen–Macaulay, provided that $R = k [ R _ { 1 }]$ and $R$ is equi-dimensional. See [a22] for the bounds of Castelnuovo–Mumford regularities of Buchsbaum schemes $X = \operatorname { Proj } R$.
Researches of the Buchsbaumness in Rees algebras recently (1999) started again, although the progress remains tardy (possibly because of the lack of characterizations of Trung–Ikeda type [a38] for Buchsbaumness). In [a14] the Buchsbaumness in Rees algebras $R ( I )$ of certain $\mathfrak{m}$-primary ideals $I$ in Cohen–Macaulay local rings is closely studied in connection with the Buchsbaumness in the associated graded rings $G ( I ) = \oplus _ { n \geq 0} I ^ { n } / I ^ { n + 1 }$ and that of the extended Rees algebras $R ^ { \prime } ( I ) = \oplus _ { n \in \bf Z} I^ { n }$. In [a26], [a41], [a42], Buchsbaumness in graded rings associated to certain $\mathfrak{m}$-primary ideals in Buchsbaum local rings is explored. Especially, the Rees algebra $R ( \mathfrak{m} )$ of the maximal ideal $\mathfrak{m}$ in a Buchsbaum local ring $A$ of maximal embedding dimension (that is, a Buchsbaum local ring $A$ for which the equality $v ( A ) = e _ { \mathfrak{m} } ^ { 0 } ( A ) + \operatorname { dim } A + I ( A ) - 1$ holds) is again a Buchsbaum ring [a42].
References
| [a1] | M. Amasaki, "Existence of homogeneous prime ideals fitting into long Bourbaki sequences" , Proc. 21st Symp. Commutative Algebra in Tokyo, Japan, November 23-26, 1999 (1999) pp. 104–111 MR1610925 |
| [a2] | J. Barshay, "Graded algebras of powers of ideals generated by A-sequences" J. Algebra , 25 (1973) pp. 90–99 MR0332748 Zbl 0256.13017 |
| [a3] | D.A. Buchsbaum, "Complexes in local ring theory" , Some Aspects of Ring Theory , C.I.M.E. Roma (1965) pp. 223–228 Zbl 0178.37201 |
| [a4] | G. Eisenbud, S. Goto, "Linear free resolutions and minimal multiplicity" J. Algebra , 88 (1984) pp. 89–133 MR0741934 Zbl 0531.13015 |
| [a5] | E.G. Evans Jr., P.A. Griffith, "Local cohomology modules for normal domains" J. London Math. Soc. , 19 (1979) pp. 277–284 MR0533326 Zbl 0407.13019 |
| [a6] | S. Goto, "On Buchsbaum rings" J. Algebra , 67 (1980) pp. 272–279 MR0602063 Zbl 0473.13010 Zbl 0473.13009 Zbl 0413.13012 |
| [a7] | S. Goto, "Blowing-up of Buchsbaum rings" , Commutative Algebra , Lecture Notes , 72 , London Math. Soc. (1981) pp. 140–162 MR0693633 Zbl 0519.13021 |
| [a8] | S. Goto, "Buchsbaum rings with multiplicity 2" J. Algebra , 74 (1982) pp. 494–508 MR0647250 Zbl 0479.13007 |
| [a9] | S. Goto, "Buchsbaum rings of maximal embedding dimension" J. Algebra , 76 (1982) pp. 383–399 MR0661862 Zbl 0482.13012 |
| [a10] | S. Goto, "On the associated graded rings of parameter ideals in Buchsbaum rings" J. Algebra , 85 (1983) pp. 490–534 MR0725097 Zbl 0529.13010 |
| [a11] | S. Goto, "Surface singularities of finite Buchsbaum-representation type" , Commutative Algebra: Proc. Microprogram June 15–July 2 , Springer (1987) pp. 247–263 MR1015521 Zbl 0741.13015 |
| [a12] | S. Goto, "Maximal Buchsbaum modules over regular local rings and a structure theorem for generalized Cohen–Macaulay modules" M. Nagata (ed.) H. Matsumura (ed.) , Commutative Algebra and Combinatorics , Adv. Stud. Pure Math. , 11 , Kinokuniya (1987) pp. 39–46 MR0951196 Zbl 0649.13009 |
| [a13] | S. Goto, "Curve singularities of finite Buchsbaum-representation type" J. Algebra , 163 (1994) pp. 447–480 MR1262714 Zbl 0807.13007 |
| [a14] | S. Goto, "Buchsbaumness in Rees algebras associated to ideals of minimal multiplicity" J. Algebra , 213 (1999) pp. 604–661 MR1673472 Zbl 0942.13003 |
| [a15] | S. Goto, K. Nishida, "Rings with only finitely many isomorphism classes of indecomposable maximal Buchsbaum modules" J. Math. Soc. Japan , 40 (1988) pp. 501–518 MR0945349 Zbl 0657.13022 |
| [a16] | S. Goto, K. Nishida, "The Cohen–Macaulay and Gorenstein Rees algebras associated to filtrations" , Memoirs , 526 , Amer. Math. Soc. (1994) MR1287443 Zbl 0812.13016 |
| [a17] | S. Goto, Y. Nakamura, K. Nishida, "Cohen–Macaulay graded rings associated ideals" Amer. J. Math. , 118 (1996) pp. 1197–1213 Zbl 0878.13002 |
| [a18] | S. Goto, Y. Shimoda, "On the Rees algebras of Cohen–Macaulay local rings" R.N. Draper (ed.) , Commutative Algebra, Analytic Methods , Lecture Notes in Pure Applied Math. , 68 , M. Dekker (1982) pp. 201–231 MR0655805 Zbl 0482.13011 |
| [a19] | S. Goto, Y. Shimoda, "On Rees algebras over Buchsbaum rings" J. Math. Kyoto Univ. , 20 (1980) pp. 691–708 MR0592354 Zbl 0473.13010 |
| [a20] | S. Goto, K. Yamagishi, "The theory of unconditioned strong $d$-sequences and modules of finite local cohomology" Preprint (1978) |
| [a21] | C. Huneke, "The theory of d-sequences and powers of ideals" Adv. Math. , 46 (1982) pp. 249–279 MR0683201 Zbl 0505.13004 |
| [a22] | L.T. Hoa, C. Miyazaki, "Bounds on Castelnuovo–Mumford regularity for generalized Cohen–Macaulay graded rings" Math. Ann. , 301 (1995) pp. 587–598 MR1324528 Zbl 0834.13016 |
| [a23] | M.-N. Ishida, "Tsuchihashi's cusp singularities are Buchsbaum singularities" Tôhoku Math. J. , 36 (1984) pp. 191–201 MR742594 |
| [a24] | T. Kawasaki, "Local cohomology modules of indecomposable surjective–Buchsbaum modules over Gorenstein local rings" J. Math. Soc. Japan , 48 (1996) pp. 551–566 MR1389995 Zbl 0866.13007 |
| [a25] | T. Kawasaki, "Arithmetic Cohen–Macaulayfications of local rings" , Proc. 21st Symp. Commutative Algebra in Tokyo, Japan, November 23-26, 1999 (1999) pp. 88–92 |
| [a26] | Y. Nakamura, "On the Buchsbaum property of associated graded rings" J. Algebra , 209 (1998) pp. 345–366 MR1652142 Zbl 0942.13002 |
| [a27] | P. Schenzel, N.V. Trung, N.T. Cuong, "Verallgemeinerte Cohen–Macaulay-Moduln" Math. Nachr. , 85 (1978) pp. 57–73 MR0517641 Zbl 0398.13014 |
| [a28] | J. Stückrad, W. Vogel, "Ein Korrekturglied in der Multiplizitätstheorie von D.G. Northcott und Anwendungen" Monatsh. Math. , 76 (1972) pp. 264–271 Zbl 0248.13026 |
| [a29] | J. Stückrad, W. Vogel, "Eine Verallgemeinerung der Cohen–Macaulay-Ringe und Anwendungen auf ein Problem der Multiplitätstheorie" J. Math. Kyoto Univ. , 13 (1973) pp. 513–528 |
| [a30] | J. Stückrad, W. Vogel, "Toward a theory of Buchsbaum singularities" Amer. J. Math. , 100 (1978) pp. 727–746 MR0509072 Zbl 0429.14001 |
| [a31] | J. Stückrad, W. Vogel, "Buchsbaum rings and applications" , Springer (1986) MR0881220 MR0873945 Zbl 0606.13018 Zbl 0606.13017 |
| [a32] | P. Schenzel, "Dualisierende Komplexe in der lokalen Algebra und Buchsbaum–Ringe" , Lecture Notes in Mathematics , 907 , Springer (1982) MR0654151 Zbl 0484.13016 |
| [a33] | P. Schenzel, "On Veronesean embeddings and projections of Veronesean varieties" Archiv Math. , 30 (1978) pp. 391–397 MR0485849 Zbl 0417.14040 |
| [a34] | R.Y. Sharp, "Necessary conditions for the existence of dualizing complexes in commutative algebra" , Lecture Notes in Mathematics , 740 , Springer (1979) pp. 213–229 MR0563505 Zbl 0421.13003 |
| [a35] | Y. Shimoda, "A note on Rees algebras of two-dimensional local domains" J. Math. Kyoto Univ. , 19 (1979) pp. 327–333 MR0545713 Zbl 0447.13010 |
| [a36] | J. Stückrad, "On the Buchsbaum property of Rees and form modules" Beitr. Algebra Geom. , 19 (1985) pp. 83–103 MR0785248 Zbl 0567.13008 |
| [a37] | N.V. Trung, "Toward a theory of generalized Cohen–Macaulay modules" Nagoya Math. J. , 102 (1986) pp. 1–49 Zbl 0649.13008 Zbl 0637.13013 |
| [a38] | N.V. Trung, S. Ikeda, "When is the Rees algebra Cohen–Macaulay?" Commun. Algebra , 17 (1989) pp. 2893–2922 Zbl 0696.13015 |
| [a39] | W. Vasconcelos, "Arithmetic of blowup algebras" , London Math. Soc. Lecture Notes , 195 , Cambridge Univ. Press (1994) MR1275840 Zbl 0813.13008 |
| [a40] | Y. Yoshino, "Maximal Buchsbaum modules of finite projective dimension" J. Algebra , 159 (1993) pp. 240–264 MR1231212 Zbl 0791.13009 |
| [a41] | K. Yamagishi, "The associated graded modules of Buchsbaum modules with respect to $\mathfrak{m}$-primary ideals in equi-I-invariant case" J. Algebra , 225 (2000) pp. 1–27 MR1743648 |
| [a42] | K. Yamagishi, "Buchsbaumness in Rees algebras associated to $\mathfrak{m}$-primary ideals of minimal multiplicity in Buchsbaum local rings" , Proc. 21st Symp. Commutative Algebra in Tokyo, Japan, November 23-26, 1999 (1999) pp. 39–45 |
Buchsbaum ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Buchsbaum_ring&oldid=16254