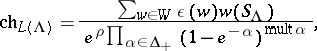|
|
| Line 1: |
Line 1: |
| | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. |
| | + | |
| | + | Out of 204 formulas, 199 were replaced by TEX code.--> |
| | + | |
| | + | {{TEX|semi-auto}}{{TEX|partial}} |
| | ''Borcherds algebra'' | | ''Borcherds algebra'' |
| | | | |
| − | While a [[Kac–Moody algebra|Kac–Moody algebra]] is generated in a fairly simple way from copies of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302001.png" />, a Borcherds or generalized Kac–Moody algebra [[#References|[a1]]], [[#References|[a7]]], [[#References|[a9]]], [[#References|[a11]]] can also involve copies of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302002.png" />-dimensional Heisenberg algebra. Nevertheless, it inherits many of the Kac–Moody properties. Borcherds algebras played a key role in the proof of the [[Moonshine conjectures|Monstrous Moonshine conjectures]] [[#References|[a4]]], and also led to the development of a theory of automorphic products [[#References|[a5]]]. | + | While a [[Kac–Moody algebra|Kac–Moody algebra]] is generated in a fairly simple way from copies of $\operatorname{sl} _ { 2 }$, a Borcherds or generalized Kac–Moody algebra [[#References|[a1]]], [[#References|[a7]]], [[#References|[a9]]], [[#References|[a11]]] can also involve copies of the $3$-dimensional Heisenberg algebra. Nevertheless, it inherits many of the Kac–Moody properties. Borcherds algebras played a key role in the proof of the [[Moonshine conjectures|Monstrous Moonshine conjectures]] [[#References|[a4]]], and also led to the development of a theory of automorphic products [[#References|[a5]]]. |
| | | | |
| − | First recall the definition of a Kac–Moody algebra. By a (symmetrizable) Cartan matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302003.png" /> one means an integral <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302004.png" />-matrix obeying | + | First recall the definition of a Kac–Moody algebra. By a (symmetrizable) Cartan matrix $A = ( a _ { ij} )$ one means an integral $( \text{l} \times \text{l} )$-matrix obeying |
| | | | |
| − | C1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302005.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302006.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302007.png" />; and | + | C1) $a _ { i i } = 2$ and $a _ { i j } \leq 0$ for all $i \neq j$; and |
| | | | |
| − | C2) there is a diagonal matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302008.png" /> with each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302009.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020010.png" /> is symmetric. A (symmetrizable) Kac–Moody algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020011.png" /> [[#References|[a10]]], [[#References|[a12]]] is the [[Lie algebra|Lie algebra]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020012.png" /> generators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020013.png" />, obeying the relations: | + | C2) there is a diagonal matrix $D$ with each $d_{ ii} > 0$ such that $D A$ is symmetric. A (symmetrizable) Kac–Moody algebra $\mathfrak { g } = \mathfrak { g } ( A )$ [[#References|[a10]]], [[#References|[a12]]] is the [[Lie algebra|Lie algebra]] on $3\text{l}$ generators $e _ { i } , f _ { i } , h _ { i }$, obeying the relations: |
| | | | |
| − | R1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020014.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020015.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020016.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020017.png" />, for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020018.png" />; and | + | R1) $[ e _ { i } f _ { j } ] = \delta _ { i j } h _ { i }$, $[ h _ { i } e _ { j } ] = a _ { ij } e _ { j }$, $[ h _ { i } f _ { j } ] = - a _ { ij } f _ { j }$, and $[ h _ { i } h _ { j } ] = 0$, for all $i , j$; and |
| | | | |
| − | R2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020019.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020020.png" />. | + | R2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020019.png"/> for all $i \neq j$. |
| | | | |
| − | A Borcherds algebra is defined similarly. By a generalized Cartan matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020021.png" /> one means a (possibly infinite) matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020022.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020023.png" />, obeying | + | A Borcherds algebra is defined similarly. By a generalized Cartan matrix $A$ one means a (possibly infinite) matrix $A = ( a _ { ij} )$, $a _ { i j } \in \mathbf{R}$, obeying |
| | | | |
| − | GC1) either <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020024.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020025.png" />; | + | GC1) either $a _ { i i } = 2$ or $a _ { i i } \leq 0$; |
| | | | |
| − | GC2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020026.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020027.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020028.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020029.png" />; and | + | GC2) $a _ { i j } \leq 0$ for $i \neq j$, and $a _ { i j } \in \mathbf{Z}$ when $a _ { i i } = 2$; and |
| | | | |
| − | GC3) there is a diagonal matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020030.png" /> with each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020031.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020032.png" /> is symmetric. By the (symmetrizable) universal Borcherds algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020033.png" /> one means the [[Lie algebra|Lie algebra]] (over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020034.png" /> say) with generators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020035.png" />, subject to the relations [[#References|[a3]]]: | + | GC3) there is a diagonal matrix $D$ with each $d_{ ii} > 0$ such that $D A$ is symmetric. By the (symmetrizable) universal Borcherds algebra $\hat { \mathfrak { g } } = \hat{\mathfrak { g } }( A )$ one means the [[Lie algebra|Lie algebra]] (over $\mathbf{R}$ say) with generators $e _ { i } , f _ { i } , h _ { i j }$, subject to the relations [[#References|[a3]]]: |
| | | | |
| − | GR1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020036.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020037.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020038.png" />, for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020039.png" />; | + | GR1) $[ e _ { i } f _ { j } ] = h _ { i j}$, $[ h _ { i j } e _ { k } ] = \delta _ { i j } a _ { i k } e _ { k }$ and $[ h _ { i j } f _ { k } ] = - \delta _ { i j } a _ { i k } f _ { k }$, for all $i , j$; |
| | | | |
| − | GR2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020040.png" />, whenever both <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020041.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020042.png" />; and | + | GR2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020040.png"/>, whenever both $a _ { i i } = 2$ and $i \neq j$; and |
| | | | |
| − | GR3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020043.png" /> whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020044.png" />. | + | GR3) $[ e _ { i } e _ { j } ] = [ f _ { i } f _ { j } ] = 0$ whenever $a _ { i j } = 0$. |
| | | | |
| − | Note that for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020045.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020046.png" /> is isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020047.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020048.png" />, and to the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020049.png" />-dimensional Heisenberg algebra when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020050.png" />. Immediate consequences of the definition are that: | + | Note that for each $i$, $\operatorname { span } \{ e _ { i } , f _ { i } , h _ { i i } \}$ is isomorphic to $\operatorname{sl} _ { 2 } ( {\bf R} )$ when $a _ { i i } \neq 0$, and to the $3$-dimensional Heisenberg algebra when $a _ { i i } = 0$. Immediate consequences of the definition are that: |
| | | | |
| − | i) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020051.png" />; | + | i) $[ h _ { i j } , h _ { m n } ] = 0$; |
| | | | |
| − | ii) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020052.png" /> unless the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020053.png" />th and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020054.png" />th column of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020055.png" /> are identical; | + | ii) $h _ { i j } = 0$ unless the $i$th and $j$th column of $A$ are identical; |
| | | | |
| − | iii) the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020056.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020057.png" /> lie in the centre of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020058.png" />. Setting all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020059.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020060.png" /> gives the definition of the (symmetrizable) Borcherds algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020061.png" /> [[#References|[a1]]]. This central extension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020062.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020063.png" /> is introduced for its role in the characterization of Borcherds algebras below. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020064.png" /> has no zero columns, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020065.png" /> equals its own universal central extension [[#References|[a3]]]. An important technical point is that both <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020066.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020067.png" /> have trivial radical. | + | iii) the $h _ { i j }$ for $i \neq j$ lie in the centre of $\hat { \mathfrak{g} }$. Setting all $h _ { i j } = 0$ for $i \neq j$ gives the definition of the (symmetrizable) Borcherds algebra $\mathfrak { g } = \mathfrak { g } ( A )$ [[#References|[a1]]]. This central extension $\hat { \mathfrak{g} }$ of $\frak g$ is introduced for its role in the characterization of Borcherds algebras below. If $A$ has no zero columns, then $\hat { \mathfrak{g} }$ equals its own universal central extension [[#References|[a3]]]. An important technical point is that both $\mathfrak { g } ( A )$ and $\hat { \mathfrak { g } } ( A )$ have trivial radical. |
| | | | |
| − | The basic structure theorem [[#References|[a1]]] is that of Kac–Moody algebras. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020068.png" /> be a symmetrizable Borcherds algebra. Then: | + | The basic structure theorem [[#References|[a1]]] is that of Kac–Moody algebras. Let $\mathfrak { g } = \mathfrak { g } ( A )$ be a symmetrizable Borcherds algebra. Then: |
| | | | |
| − | a) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020069.png" /> has triangular decomposition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020070.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020071.png" /> is the subalgebra generated by the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020072.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020073.png" /> is generated by the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020074.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020075.png" /> is the [[Cartan subalgebra|Cartan subalgebra]]. Also, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020076.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020077.png" />. | + | a) $\frak g$ has triangular decomposition $\mathfrak { g } = \mathfrak { g } _ { + } \oplus \mathfrak { h } \oplus \mathfrak { g } _ { - }$, where $\mathfrak { g }_{ +}$ is the subalgebra generated by the $e _ { i }$, $\mathfrak{g}_{-}$ is generated by the $f_i$, and $\mathfrak { h } = \operatorname { span } \{ h _ { i } \}$ is the [[Cartan subalgebra|Cartan subalgebra]]. Also, $[ \mathfrak { g } _ { + } , \mathfrak { g } _ { - } ] \subset \mathfrak { h }$ and $[ \mathfrak { h } , \mathfrak { g } _ { \pm } ] \subset \mathfrak { g } _ { \pm }$. |
| | | | |
| − | b) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020078.png" /> has a root space decomposition: formally calling <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020079.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020080.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020081.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020082.png" />, and defining <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020083.png" /> to be the subspace of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020084.png" />, one gets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020085.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020086.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020087.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020088.png" />; | + | b) $\frak g$ has a root space decomposition: formally calling $e _ { i }$ <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020080.png"/> and $f_i$ $\text{degree}- \alpha_{i}$, and defining $\mathfrak { g } ^ { \alpha }$ to be the subspace of degree $\alpha \in \mathbf{Z} \alpha _ { 1 } + \mathbf{Z} \alpha _ { 2 } + \dots$, one gets $\mathfrak { h } = \mathfrak { g } ^ { 0 }$ and $\mathfrak { g } _ { \pm } = \oplus _ { \alpha \in \Delta _ { \pm } } \mathfrak { g } ^ { \alpha }$, where $[ \mathfrak { g } ^ { \alpha } , \mathfrak { g } ^ { \beta } ] \subset \mathfrak { g } ^ { \alpha + \beta}$ and $\Delta _ { - } = - \Delta _ { + }$; |
| | | | |
| − | c) there is an involution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020089.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020090.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020091.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020092.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020093.png" />; | + | c) there is an involution $\omega$ on $\frak g$ for which $\omega e _ { i } = f _ { i }$, $\omega h _ { i } = - h_i$, and $\omega \mathfrak { g } ^ { \alpha } = \mathfrak { g } ^ { - \alpha}$; |
| | | | |
| − | d) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020094.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020095.png" />; | + | d) $\operatorname{ dim} \mathfrak { g } ^ { \alpha } < \infty$ and $\operatorname { dim } \mathfrak { g } ^ { \pm \alpha _ { i }} = 1$; |
| | | | |
| − | e) there is an invariant symmetric bilinear form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020096.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020097.png" /> such that for each root <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020098.png" />, the restriction of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b13020099.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200100.png" /> is non-degenerate, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200101.png" /> whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200102.png" />; | + | e) there is an invariant symmetric bilinear form $( . | . )$ on $\frak g$ such that for each root $\alpha \neq 0$, the restriction of $( . | . )$ to $\mathfrak { g } ^ { \alpha } \times \mathfrak { g } ^ { - \alpha }$ is non-degenerate, and $( \mathfrak { g } ^ { \alpha } | \mathfrak { g } ^ { \beta } ) = 0$ whenever $\beta \neq - \alpha$; |
| | | | |
| − | f) there is a linear assignment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200103.png" /> such that for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200104.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200105.png" />, one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200106.png" />. | + | f) there is a linear assignment $\alpha \mapsto x _ { \alpha } \in \mathfrak{h}$ such that for all $a \in \mathfrak { g } ^ { \alpha }$, $b \in \mathfrak { g } ^ { - \alpha }$, one has $[ a , b ] = ( a | b ) x _ { \alpha }$. |
| | | | |
| − | The condition that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200107.png" /> be symmetrizable (i.e. condition GC3)) is necessary for the existence of the bilinear form in e). For representation theory it is common to add derivations, so that the roots <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200108.png" /> will lie in a dual space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200109.png" />. In particular, define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200110.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200111.png" />; then each linear mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200112.png" /> is a derivation, and adjoining these to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200113.png" /> defines an Abelian algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200114.png" />. The simple root <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200115.png" /> can be interpreted as the element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200116.png" /> obeying <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200117.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200118.png" />. Construct the induced bilinear form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200119.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200120.png" />, obeying <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200121.png" />. | + | The condition that $\frak g$ be symmetrizable (i.e. condition GC3)) is necessary for the existence of the bilinear form in e). For representation theory it is common to add derivations, so that the roots $\alpha$ will lie in a dual space ${\frak h} ^ { e ^ { * } }$. In particular, define $D _ { i } ( a ) = n _ { i } a$ for any $a \in \mathfrak { g } ^ { n_1 \alpha _ { 1 } + \ldots }$; then each linear mapping $D_i$ is a derivation, and adjoining these to $\mathfrak h $ defines an Abelian algebra $\mathfrak{h} ^ {e }$. The simple root $\alpha_i$ can be interpreted as the element of ${\frak h} ^ { e ^ { * } }$ obeying $\alpha _ { j } ( h _ { i } ) = a _ {i j }$ and $\alpha _ { j } ( D _ { i } ) = \delta _ { i j }$. Construct the induced bilinear form $( . | . )$ on ${\frak h} ^ { e ^ { * } }$, obeying $( \alpha _ { i } | \alpha _ { j } ) = d _ { i } a _ {i j }$. |
| | | | |
| − | The properties a)–f) characterize Borcherds algebras. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200122.png" /> be a Lie algebra (over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200123.png" />) satisfying the following conditions: | + | The properties a)–f) characterize Borcherds algebras. Let $G$ be a Lie algebra (over $\mathbf{R}$) satisfying the following conditions: |
| | | | |
| − | 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200124.png" /> has a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200125.png" />-grading <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200126.png" /> (cf. also [[Lie algebra, graded|Lie algebra, graded]]), and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200127.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200128.png" />; | + | 1) $G$ has a $\mathbf{Z}$-grading $\oplus _ { i } G_ {i}$ (cf. also [[Lie algebra, graded|Lie algebra, graded]]), and $\operatorname{dim} G _ { i } < \infty$ for all $i \neq 0$; |
| | | | |
| − | 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200129.png" /> has an involution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200130.png" /> sending <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200131.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200132.png" /> and acting as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200133.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200134.png" />; | + | 2) $G$ has an involution $\omega$ sending $G_i$ to $G_{ - i}$ and acting as $- 1$ on $G_0$; |
| | | | |
| − | 3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200135.png" /> has an invariant bilinear form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200136.png" /> invariant under <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200137.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200138.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200139.png" />, and such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200140.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200141.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200142.png" />. Then there is a homomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200143.png" /> from some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200144.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200145.png" /> whose kernel is contained in the centre of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200146.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200147.png" /> is the semi-direct product of the image of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200148.png" /> with a subalgebra of the Abelian subalgebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200149.png" />. That is, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200150.png" /> is obtained from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200151.png" /> by modding out some of the centre and adding some commuting derivations. See e.g. [[#References|[a4]]] for details. | + | 3) $G$ has an invariant bilinear form $( . | . )$ invariant under $\omega$ such that $( G _ { i } | G _ { j } ) = 0$ if $i \neq - j$, and such that $- ( a | \omega ( a ) ) > 0$ if $0 \neq a \in G _ { i }$ for $i \neq 0$. Then there is a homomorphism $\pi$ from some $\hat { \mathfrak { g } } ( A )$ to $G$ whose kernel is contained in the centre of $\hat { \mathfrak{g} }$, and $G$ is the semi-direct product of the image of $\pi$ with a subalgebra of the Abelian subalgebra $G_0$. That is, $G$ is obtained from $\hat { \mathfrak{g} }$ by modding out some of the centre and adding some commuting derivations. See e.g. [[#References|[a4]]] for details. |
| | | | |
| − | Define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200152.png" /> to be the set of all real simple roots, i.e. all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200153.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200154.png" />; the remaining simple roots are the imaginary simple roots <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200155.png" />. The Weyl group (cf. also [[Weyl group|Weyl group]]) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200156.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200157.png" /> is the group generated by the reflections <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200158.png" /> for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200159.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200160.png" />. It will be a (crystallographic) [[Coxeter group|Coxeter group]]. The real roots of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200161.png" /> are defined to be those in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200162.png" />; all other roots are called imaginary. For all real roots, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200163.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200164.png" />. | + | Define $\Pi ^ { \text { re } }$ to be the set of all real simple roots, i.e. all $\alpha_i$ with $a _ { i i } = 2$; the remaining simple roots are the imaginary simple roots $\alpha \in \Pi ^ { \operatorname {im} }$. The Weyl group (cf. also [[Weyl group|Weyl group]]) $W$ of $\frak g$ is the group generated by the reflections $r_i : \mathfrak{h}^ { e ^ { * } } \rightarrow \mathfrak{h} ^ { e ^ { * } }$ for each $\alpha _ { i } \in \Pi ^ { \text{re} }$: $r ( \lambda ) = \lambda - \lambda ( h _ { i } ) \alpha _ { i }$. It will be a (crystallographic) [[Coxeter group|Coxeter group]]. The real roots of $\frak g$ are defined to be those in $W ( \Pi ^ { re } )$; all other roots are called imaginary. For all real roots, $\operatorname { lim } \mathfrak { g } ^ { \alpha } = 1$ and $( \alpha | \alpha ) > 0$. |
| | | | |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200165.png" /> is called an integrable module if
| + | $V$ is called an integrable module if |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200166.png" /></td> </tr></table>
| + | \begin{equation*} V = \bigoplus _ { \lambda \in \mathfrak { h } ^ { e * } } V ^ { \lambda }, \end{equation*} |
| | | | |
| − | where the weight space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200167.png" />, with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200168.png" />, and for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200169.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200170.png" /> both <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200171.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200172.png" /> are locally nilpotent: i.e. for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200173.png" /> and all sufficiently large <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200174.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200175.png" />. By the character one means the formal sum | + | where the weight space $V ^ { \lambda } : = \{ v \in V : h . v = \lambda ( h ) v \}$, with $\operatorname{dim}V^\lambda<\infty$, and for each $i$ with $a _ { i i } = 2$ both $e _ { i }$ and $f_i$ are locally nilpotent: i.e. for all $v \in V$ and all sufficiently large $k$, $( e _ { i } ) ^ { k } . v = 0 = ( f _ { i } ) ^ { k } . v$. By the character one means the formal sum |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200176.png" /></td> </tr></table>
| + | \begin{equation*} \operatorname { ch } _ { V } : = \sum _ { \lambda \in \mathfrak{h} ^ {e* } } ( \operatorname { dim } V ^ { \lambda } ) e ^ { \lambda }. \end{equation*} |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200177.png" /> be the set of all weights <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200178.png" /> obeying <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200179.png" /> whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200180.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200181.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200182.png" />. Define the highest-weight <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200184.png" />-module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200185.png" /> in the usual way as the quotient of the Verma module (cf. also [[Representation of a Lie algebra|Representation of a Lie algebra]]) by the unique proper graded submodule. Then one obtains the Weyl–Kac–Borcherds character formula: Choose <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200186.png" /> to satisfy | + | Let $P _ { + }$ be the set of all weights $\Lambda \in \mathfrak { h } ^ { * }$ obeying $\Lambda ( h _ { i } ) \in {\bf Z}_{ \geq 0}$ whenever $a _ { i i } = 2$, and $\Lambda ( h _ { i } ) \geq 0$ for all $i$. Define the highest-weight $\frak g$-module $L ( \Lambda )$ in the usual way as the quotient of the Verma module (cf. also [[Representation of a Lie algebra|Representation of a Lie algebra]]) by the unique proper graded submodule. Then one obtains the Weyl–Kac–Borcherds character formula: Choose $\rho \in \mathfrak { h } ^ { * }$ to satisfy |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200187.png" /></td> </tr></table>
| + | \begin{equation*} ( \rho \mid \alpha _ { i } ) = \frac { 1 } { 2 } ( \alpha _ { i } \mid \alpha _ { i } ) \end{equation*} |
| | | | |
| − | for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200188.png" />, and define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200189.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200190.png" /> runs over all sums of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200191.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200192.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200193.png" /> is the sum of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200194.png" /> distinct mutually orthogonal imaginary simple roots, each of which is orthogonal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200195.png" />, otherwise <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200196.png" />. Then | + | for all $i$, and define $S _ { \Lambda } = e ^ { \Lambda + \rho } \sum _ { s } \epsilon ( s ) e ^ { s }$, where $s$ runs over all sums of $\alpha _ { i } \in \Pi ^ { \text{im} }$ and $\epsilon ( s ) = ( - 1 ) ^ { m }$ if $s$ is the sum of $m$ distinct mutually orthogonal imaginary simple roots, each of which is orthogonal to $\Lambda$, otherwise $\epsilon ( s ) = 0$. Then |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200197.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200197.png"/></td> </tr></table> |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200198.png" />. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200199.png" /> is the correction factor due to imaginary simple roots, much as the "extra" terms in the Macdonald identities are due to the imaginary affine roots. Putting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200200.png" /> gives the denominator identity, as usual. | + | where $\operatorname{mult}\alpha = \dim \mathfrak{g}^\alpha$. $S _ { \Lambda }$ is the correction factor due to imaginary simple roots, much as the "extra" terms in the Macdonald identities are due to the imaginary affine roots. Putting $\Lambda = 0$ gives the denominator identity, as usual. |
| | | | |
| − | Thus, Borcherds algebras strongly resemble Kac–Moody algebras and constitute a natural and non-trivial generalization. The main differences are that they can be generated by copies of the Heisenberg algebra as well as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200201.png" />, and that there can be imaginary simple roots. | + | Thus, Borcherds algebras strongly resemble Kac–Moody algebras and constitute a natural and non-trivial generalization. The main differences are that they can be generated by copies of the Heisenberg algebra as well as $\operatorname{sl} _ { 2 } ( {\bf R} )$, and that there can be imaginary simple roots. |
| | | | |
| − | Interesting examples of Borcherds algebras are the Monster Lie algebra [[#References|[a4]]], whose (twisted) denominator identity supplied the relations needed to complete the proof of the Monstrous Moonshine conjectures, and the fake Monster [[#References|[a2]]]. A Borcherds algebra can be associated to any even Lorentzian lattice. The denominator identities of Borcherds algebras are often automorphic forms on the automorphism group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200202.png" /> of the even self-dual lattice <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200203.png" /> [[#References|[a5]]]. They can serve as "automorphic corrections" to Lorentzian Kac–Moody algebras (see, for instance, [[#References|[a6]]]). The space of BPS states in string theory carries a natural structure of a Borcherds-like algebra [[#References|[a8]]]. | + | Interesting examples of Borcherds algebras are the Monster Lie algebra [[#References|[a4]]], whose (twisted) denominator identity supplied the relations needed to complete the proof of the Monstrous Moonshine conjectures, and the fake Monster [[#References|[a2]]]. A Borcherds algebra can be associated to any even Lorentzian lattice. The denominator identities of Borcherds algebras are often automorphic forms on the automorphism group $O _ { s + 2,2} (\bf R )$ of the even self-dual lattice $\text{II} _ { s + 2,2 }$ [[#References|[a5]]]. They can serve as "automorphic corrections" to Lorentzian Kac–Moody algebras (see, for instance, [[#References|[a6]]]). The space of BPS states in string theory carries a natural structure of a Borcherds-like algebra [[#References|[a8]]]. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.E. Borcherds, "Generalized Kac–Moody algebras" ''J. Algebra'' , '''115''' (1988) pp. 501–512</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R.E. Borcherds, "The monster Lie algebra" ''Adv. Math.'' , '''83''' (1990) pp. 30–47</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R.E. Borcherds, "Central extensions of generalized Kac–Moody algebras" ''J. Algebra'' , '''140''' (1991) pp. 330–335</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> R.E. Borcherds, "Monstrous moonshine and monstrous Lie superalgebras" ''Invent. Math.'' , '''109''' (1992) pp. 405–444</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> R.E. Borcherds, "Automorphic forms on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b130200204.png" /> and infinite products" ''Invent. Math.'' , '''120''' (1995) pp. 161–213</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> V.A. Gritsenko, V.V. Nikulin, "Siegel automorphic form corrections of some Lorentzian Kac–Moody Lie algebras" ''Amer. J. Math.'' , '''119''' (1997) pp. 181–224</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> K. Harada, M. Miyamoto, H. Yamada, "A generalization of Kac–Moody algebras" , ''Groups, Difference Sets, and the Monster'' , de Gruyter (1996)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> J.A. Harvey, G. Moore, "On the algebras of BPS states" ''Commun. Math. Phys.'' , '''197''' (1998) pp. 489–519</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> E. Jurisich, "An exposition of generalized Kac–Moody algebras" ''Contemp. Math.'' , '''194''' (1996) pp. 121–159</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> V.G. Kac, "Simple irreducible graded Lie algebras of finite growth" ''Math. USSR Izv.'' , '''2''' (1968) pp. 1271–1311</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> V.G. Kac, "Infinite dimensional Lie algebras" , Cambridge Univ. Press (1990) (Edition: Third)</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> R.V. Moody, "A new class of Lie algebras" ''J. Algebra'' , '''10''' (1968) pp. 211–230</TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> R.E. Borcherds, "Generalized Kac–Moody algebras" ''J. Algebra'' , '''115''' (1988) pp. 501–512</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> R.E. Borcherds, "The monster Lie algebra" ''Adv. Math.'' , '''83''' (1990) pp. 30–47</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> R.E. Borcherds, "Central extensions of generalized Kac–Moody algebras" ''J. Algebra'' , '''140''' (1991) pp. 330–335</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> R.E. Borcherds, "Monstrous moonshine and monstrous Lie superalgebras" ''Invent. Math.'' , '''109''' (1992) pp. 405–444</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> R.E. Borcherds, "Automorphic forms on $O _ { s + 2,2} (\bf R )$ and infinite products" ''Invent. Math.'' , '''120''' (1995) pp. 161–213</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> V.A. Gritsenko, V.V. Nikulin, "Siegel automorphic form corrections of some Lorentzian Kac–Moody Lie algebras" ''Amer. J. Math.'' , '''119''' (1997) pp. 181–224</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> K. Harada, M. Miyamoto, H. Yamada, "A generalization of Kac–Moody algebras" , ''Groups, Difference Sets, and the Monster'' , de Gruyter (1996)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> J.A. Harvey, G. Moore, "On the algebras of BPS states" ''Commun. Math. Phys.'' , '''197''' (1998) pp. 489–519</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> E. Jurisich, "An exposition of generalized Kac–Moody algebras" ''Contemp. Math.'' , '''194''' (1996) pp. 121–159</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> V.G. Kac, "Simple irreducible graded Lie algebras of finite growth" ''Math. USSR Izv.'' , '''2''' (1968) pp. 1271–1311</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> V.G. Kac, "Infinite dimensional Lie algebras" , Cambridge Univ. Press (1990) (Edition: Third)</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> R.V. Moody, "A new class of Lie algebras" ''J. Algebra'' , '''10''' (1968) pp. 211–230</td></tr></table> |
Borcherds algebra
While a Kac–Moody algebra is generated in a fairly simple way from copies of $\operatorname{sl} _ { 2 }$, a Borcherds or generalized Kac–Moody algebra [a1], [a7], [a9], [a11] can also involve copies of the $3$-dimensional Heisenberg algebra. Nevertheless, it inherits many of the Kac–Moody properties. Borcherds algebras played a key role in the proof of the Monstrous Moonshine conjectures [a4], and also led to the development of a theory of automorphic products [a5].
First recall the definition of a Kac–Moody algebra. By a (symmetrizable) Cartan matrix $A = ( a _ { ij} )$ one means an integral $( \text{l} \times \text{l} )$-matrix obeying
C1) $a _ { i i } = 2$ and $a _ { i j } \leq 0$ for all $i \neq j$; and
C2) there is a diagonal matrix $D$ with each $d_{ ii} > 0$ such that $D A$ is symmetric. A (symmetrizable) Kac–Moody algebra $\mathfrak { g } = \mathfrak { g } ( A )$ [a10], [a12] is the Lie algebra on $3\text{l}$ generators $e _ { i } , f _ { i } , h _ { i }$, obeying the relations:
R1) $[ e _ { i } f _ { j } ] = \delta _ { i j } h _ { i }$, $[ h _ { i } e _ { j } ] = a _ { ij } e _ { j }$, $[ h _ { i } f _ { j } ] = - a _ { ij } f _ { j }$, and $[ h _ { i } h _ { j } ] = 0$, for all $i , j$; and
R2) 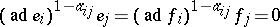 for all $i \neq j$.
for all $i \neq j$.
A Borcherds algebra is defined similarly. By a generalized Cartan matrix $A$ one means a (possibly infinite) matrix $A = ( a _ { ij} )$, $a _ { i j } \in \mathbf{R}$, obeying
GC1) either $a _ { i i } = 2$ or $a _ { i i } \leq 0$;
GC2) $a _ { i j } \leq 0$ for $i \neq j$, and $a _ { i j } \in \mathbf{Z}$ when $a _ { i i } = 2$; and
GC3) there is a diagonal matrix $D$ with each $d_{ ii} > 0$ such that $D A$ is symmetric. By the (symmetrizable) universal Borcherds algebra $\hat { \mathfrak { g } } = \hat{\mathfrak { g } }( A )$ one means the Lie algebra (over $\mathbf{R}$ say) with generators $e _ { i } , f _ { i } , h _ { i j }$, subject to the relations [a3]:
GR1) $[ e _ { i } f _ { j } ] = h _ { i j}$, $[ h _ { i j } e _ { k } ] = \delta _ { i j } a _ { i k } e _ { k }$ and $[ h _ { i j } f _ { k } ] = - \delta _ { i j } a _ { i k } f _ { k }$, for all $i , j$;
GR2) 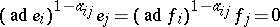 , whenever both $a _ { i i } = 2$ and $i \neq j$; and
, whenever both $a _ { i i } = 2$ and $i \neq j$; and
GR3) $[ e _ { i } e _ { j } ] = [ f _ { i } f _ { j } ] = 0$ whenever $a _ { i j } = 0$.
Note that for each $i$, $\operatorname { span } \{ e _ { i } , f _ { i } , h _ { i i } \}$ is isomorphic to $\operatorname{sl} _ { 2 } ( {\bf R} )$ when $a _ { i i } \neq 0$, and to the $3$-dimensional Heisenberg algebra when $a _ { i i } = 0$. Immediate consequences of the definition are that:
i) $[ h _ { i j } , h _ { m n } ] = 0$;
ii) $h _ { i j } = 0$ unless the $i$th and $j$th column of $A$ are identical;
iii) the $h _ { i j }$ for $i \neq j$ lie in the centre of $\hat { \mathfrak{g} }$. Setting all $h _ { i j } = 0$ for $i \neq j$ gives the definition of the (symmetrizable) Borcherds algebra $\mathfrak { g } = \mathfrak { g } ( A )$ [a1]. This central extension $\hat { \mathfrak{g} }$ of $\frak g$ is introduced for its role in the characterization of Borcherds algebras below. If $A$ has no zero columns, then $\hat { \mathfrak{g} }$ equals its own universal central extension [a3]. An important technical point is that both $\mathfrak { g } ( A )$ and $\hat { \mathfrak { g } } ( A )$ have trivial radical.
The basic structure theorem [a1] is that of Kac–Moody algebras. Let $\mathfrak { g } = \mathfrak { g } ( A )$ be a symmetrizable Borcherds algebra. Then:
a) $\frak g$ has triangular decomposition $\mathfrak { g } = \mathfrak { g } _ { + } \oplus \mathfrak { h } \oplus \mathfrak { g } _ { - }$, where $\mathfrak { g }_{ +}$ is the subalgebra generated by the $e _ { i }$, $\mathfrak{g}_{-}$ is generated by the $f_i$, and $\mathfrak { h } = \operatorname { span } \{ h _ { i } \}$ is the Cartan subalgebra. Also, $[ \mathfrak { g } _ { + } , \mathfrak { g } _ { - } ] \subset \mathfrak { h }$ and $[ \mathfrak { h } , \mathfrak { g } _ { \pm } ] \subset \mathfrak { g } _ { \pm }$.
b) $\frak g$ has a root space decomposition: formally calling $e _ { i }$ 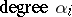 and $f_i$ $\text{degree}- \alpha_{i}$, and defining $\mathfrak { g } ^ { \alpha }$ to be the subspace of degree $\alpha \in \mathbf{Z} \alpha _ { 1 } + \mathbf{Z} \alpha _ { 2 } + \dots$, one gets $\mathfrak { h } = \mathfrak { g } ^ { 0 }$ and $\mathfrak { g } _ { \pm } = \oplus _ { \alpha \in \Delta _ { \pm } } \mathfrak { g } ^ { \alpha }$, where $[ \mathfrak { g } ^ { \alpha } , \mathfrak { g } ^ { \beta } ] \subset \mathfrak { g } ^ { \alpha + \beta}$ and $\Delta _ { - } = - \Delta _ { + }$;
and $f_i$ $\text{degree}- \alpha_{i}$, and defining $\mathfrak { g } ^ { \alpha }$ to be the subspace of degree $\alpha \in \mathbf{Z} \alpha _ { 1 } + \mathbf{Z} \alpha _ { 2 } + \dots$, one gets $\mathfrak { h } = \mathfrak { g } ^ { 0 }$ and $\mathfrak { g } _ { \pm } = \oplus _ { \alpha \in \Delta _ { \pm } } \mathfrak { g } ^ { \alpha }$, where $[ \mathfrak { g } ^ { \alpha } , \mathfrak { g } ^ { \beta } ] \subset \mathfrak { g } ^ { \alpha + \beta}$ and $\Delta _ { - } = - \Delta _ { + }$;
c) there is an involution $\omega$ on $\frak g$ for which $\omega e _ { i } = f _ { i }$, $\omega h _ { i } = - h_i$, and $\omega \mathfrak { g } ^ { \alpha } = \mathfrak { g } ^ { - \alpha}$;
d) $\operatorname{ dim} \mathfrak { g } ^ { \alpha } < \infty$ and $\operatorname { dim } \mathfrak { g } ^ { \pm \alpha _ { i }} = 1$;
e) there is an invariant symmetric bilinear form $( . | . )$ on $\frak g$ such that for each root $\alpha \neq 0$, the restriction of $( . | . )$ to $\mathfrak { g } ^ { \alpha } \times \mathfrak { g } ^ { - \alpha }$ is non-degenerate, and $( \mathfrak { g } ^ { \alpha } | \mathfrak { g } ^ { \beta } ) = 0$ whenever $\beta \neq - \alpha$;
f) there is a linear assignment $\alpha \mapsto x _ { \alpha } \in \mathfrak{h}$ such that for all $a \in \mathfrak { g } ^ { \alpha }$, $b \in \mathfrak { g } ^ { - \alpha }$, one has $[ a , b ] = ( a | b ) x _ { \alpha }$.
The condition that $\frak g$ be symmetrizable (i.e. condition GC3)) is necessary for the existence of the bilinear form in e). For representation theory it is common to add derivations, so that the roots $\alpha$ will lie in a dual space ${\frak h} ^ { e ^ { * } }$. In particular, define $D _ { i } ( a ) = n _ { i } a$ for any $a \in \mathfrak { g } ^ { n_1 \alpha _ { 1 } + \ldots }$; then each linear mapping $D_i$ is a derivation, and adjoining these to $\mathfrak h $ defines an Abelian algebra $\mathfrak{h} ^ {e }$. The simple root $\alpha_i$ can be interpreted as the element of ${\frak h} ^ { e ^ { * } }$ obeying $\alpha _ { j } ( h _ { i } ) = a _ {i j }$ and $\alpha _ { j } ( D _ { i } ) = \delta _ { i j }$. Construct the induced bilinear form $( . | . )$ on ${\frak h} ^ { e ^ { * } }$, obeying $( \alpha _ { i } | \alpha _ { j } ) = d _ { i } a _ {i j }$.
The properties a)–f) characterize Borcherds algebras. Let $G$ be a Lie algebra (over $\mathbf{R}$) satisfying the following conditions:
1) $G$ has a $\mathbf{Z}$-grading $\oplus _ { i } G_ {i}$ (cf. also Lie algebra, graded), and $\operatorname{dim} G _ { i } < \infty$ for all $i \neq 0$;
2) $G$ has an involution $\omega$ sending $G_i$ to $G_{ - i}$ and acting as $- 1$ on $G_0$;
3) $G$ has an invariant bilinear form $( . | . )$ invariant under $\omega$ such that $( G _ { i } | G _ { j } ) = 0$ if $i \neq - j$, and such that $- ( a | \omega ( a ) ) > 0$ if $0 \neq a \in G _ { i }$ for $i \neq 0$. Then there is a homomorphism $\pi$ from some $\hat { \mathfrak { g } } ( A )$ to $G$ whose kernel is contained in the centre of $\hat { \mathfrak{g} }$, and $G$ is the semi-direct product of the image of $\pi$ with a subalgebra of the Abelian subalgebra $G_0$. That is, $G$ is obtained from $\hat { \mathfrak{g} }$ by modding out some of the centre and adding some commuting derivations. See e.g. [a4] for details.
Define $\Pi ^ { \text { re } }$ to be the set of all real simple roots, i.e. all $\alpha_i$ with $a _ { i i } = 2$; the remaining simple roots are the imaginary simple roots $\alpha \in \Pi ^ { \operatorname {im} }$. The Weyl group (cf. also Weyl group) $W$ of $\frak g$ is the group generated by the reflections $r_i : \mathfrak{h}^ { e ^ { * } } \rightarrow \mathfrak{h} ^ { e ^ { * } }$ for each $\alpha _ { i } \in \Pi ^ { \text{re} }$: $r ( \lambda ) = \lambda - \lambda ( h _ { i } ) \alpha _ { i }$. It will be a (crystallographic) Coxeter group. The real roots of $\frak g$ are defined to be those in $W ( \Pi ^ { re } )$; all other roots are called imaginary. For all real roots, $\operatorname { lim } \mathfrak { g } ^ { \alpha } = 1$ and $( \alpha | \alpha ) > 0$.
$V$ is called an integrable module if
\begin{equation*} V = \bigoplus _ { \lambda \in \mathfrak { h } ^ { e * } } V ^ { \lambda }, \end{equation*}
where the weight space $V ^ { \lambda } : = \{ v \in V : h . v = \lambda ( h ) v \}$, with $\operatorname{dim}V^\lambda<\infty$, and for each $i$ with $a _ { i i } = 2$ both $e _ { i }$ and $f_i$ are locally nilpotent: i.e. for all $v \in V$ and all sufficiently large $k$, $( e _ { i } ) ^ { k } . v = 0 = ( f _ { i } ) ^ { k } . v$. By the character one means the formal sum
\begin{equation*} \operatorname { ch } _ { V } : = \sum _ { \lambda \in \mathfrak{h} ^ {e* } } ( \operatorname { dim } V ^ { \lambda } ) e ^ { \lambda }. \end{equation*}
Let $P _ { + }$ be the set of all weights $\Lambda \in \mathfrak { h } ^ { * }$ obeying $\Lambda ( h _ { i } ) \in {\bf Z}_{ \geq 0}$ whenever $a _ { i i } = 2$, and $\Lambda ( h _ { i } ) \geq 0$ for all $i$. Define the highest-weight $\frak g$-module $L ( \Lambda )$ in the usual way as the quotient of the Verma module (cf. also Representation of a Lie algebra) by the unique proper graded submodule. Then one obtains the Weyl–Kac–Borcherds character formula: Choose $\rho \in \mathfrak { h } ^ { * }$ to satisfy
\begin{equation*} ( \rho \mid \alpha _ { i } ) = \frac { 1 } { 2 } ( \alpha _ { i } \mid \alpha _ { i } ) \end{equation*}
for all $i$, and define $S _ { \Lambda } = e ^ { \Lambda + \rho } \sum _ { s } \epsilon ( s ) e ^ { s }$, where $s$ runs over all sums of $\alpha _ { i } \in \Pi ^ { \text{im} }$ and $\epsilon ( s ) = ( - 1 ) ^ { m }$ if $s$ is the sum of $m$ distinct mutually orthogonal imaginary simple roots, each of which is orthogonal to $\Lambda$, otherwise $\epsilon ( s ) = 0$. Then
where $\operatorname{mult}\alpha = \dim \mathfrak{g}^\alpha$. $S _ { \Lambda }$ is the correction factor due to imaginary simple roots, much as the "extra" terms in the Macdonald identities are due to the imaginary affine roots. Putting $\Lambda = 0$ gives the denominator identity, as usual.
Thus, Borcherds algebras strongly resemble Kac–Moody algebras and constitute a natural and non-trivial generalization. The main differences are that they can be generated by copies of the Heisenberg algebra as well as $\operatorname{sl} _ { 2 } ( {\bf R} )$, and that there can be imaginary simple roots.
Interesting examples of Borcherds algebras are the Monster Lie algebra [a4], whose (twisted) denominator identity supplied the relations needed to complete the proof of the Monstrous Moonshine conjectures, and the fake Monster [a2]. A Borcherds algebra can be associated to any even Lorentzian lattice. The denominator identities of Borcherds algebras are often automorphic forms on the automorphism group $O _ { s + 2,2} (\bf R )$ of the even self-dual lattice $\text{II} _ { s + 2,2 }$ [a5]. They can serve as "automorphic corrections" to Lorentzian Kac–Moody algebras (see, for instance, [a6]). The space of BPS states in string theory carries a natural structure of a Borcherds-like algebra [a8].
References
| [a1] | R.E. Borcherds, "Generalized Kac–Moody algebras" J. Algebra , 115 (1988) pp. 501–512 |
| [a2] | R.E. Borcherds, "The monster Lie algebra" Adv. Math. , 83 (1990) pp. 30–47 |
| [a3] | R.E. Borcherds, "Central extensions of generalized Kac–Moody algebras" J. Algebra , 140 (1991) pp. 330–335 |
| [a4] | R.E. Borcherds, "Monstrous moonshine and monstrous Lie superalgebras" Invent. Math. , 109 (1992) pp. 405–444 |
| [a5] | R.E. Borcherds, "Automorphic forms on $O _ { s + 2,2} (\bf R )$ and infinite products" Invent. Math. , 120 (1995) pp. 161–213 |
| [a6] | V.A. Gritsenko, V.V. Nikulin, "Siegel automorphic form corrections of some Lorentzian Kac–Moody Lie algebras" Amer. J. Math. , 119 (1997) pp. 181–224 |
| [a7] | K. Harada, M. Miyamoto, H. Yamada, "A generalization of Kac–Moody algebras" , Groups, Difference Sets, and the Monster , de Gruyter (1996) |
| [a8] | J.A. Harvey, G. Moore, "On the algebras of BPS states" Commun. Math. Phys. , 197 (1998) pp. 489–519 |
| [a9] | E. Jurisich, "An exposition of generalized Kac–Moody algebras" Contemp. Math. , 194 (1996) pp. 121–159 |
| [a10] | V.G. Kac, "Simple irreducible graded Lie algebras of finite growth" Math. USSR Izv. , 2 (1968) pp. 1271–1311 |
| [a11] | V.G. Kac, "Infinite dimensional Lie algebras" , Cambridge Univ. Press (1990) (Edition: Third) |
| [a12] | R.V. Moody, "A new class of Lie algebras" J. Algebra , 10 (1968) pp. 211–230 |
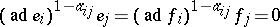 for all $i \neq j$.
for all $i \neq j$.
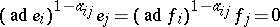 , whenever both $a _ { i i } = 2$ and $i \neq j$; and
, whenever both $a _ { i i } = 2$ and $i \neq j$; and
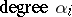 and $f_i$ $\text{degree}- \alpha_{i}$, and defining $\mathfrak { g } ^ { \alpha }$ to be the subspace of degree $\alpha \in \mathbf{Z} \alpha _ { 1 } + \mathbf{Z} \alpha _ { 2 } + \dots$, one gets $\mathfrak { h } = \mathfrak { g } ^ { 0 }$ and $\mathfrak { g } _ { \pm } = \oplus _ { \alpha \in \Delta _ { \pm } } \mathfrak { g } ^ { \alpha }$, where $[ \mathfrak { g } ^ { \alpha } , \mathfrak { g } ^ { \beta } ] \subset \mathfrak { g } ^ { \alpha + \beta}$ and $\Delta _ { - } = - \Delta _ { + }$;
and $f_i$ $\text{degree}- \alpha_{i}$, and defining $\mathfrak { g } ^ { \alpha }$ to be the subspace of degree $\alpha \in \mathbf{Z} \alpha _ { 1 } + \mathbf{Z} \alpha _ { 2 } + \dots$, one gets $\mathfrak { h } = \mathfrak { g } ^ { 0 }$ and $\mathfrak { g } _ { \pm } = \oplus _ { \alpha \in \Delta _ { \pm } } \mathfrak { g } ^ { \alpha }$, where $[ \mathfrak { g } ^ { \alpha } , \mathfrak { g } ^ { \beta } ] \subset \mathfrak { g } ^ { \alpha + \beta}$ and $\Delta _ { - } = - \Delta _ { + }$;