|
|
| Line 1: |
Line 1: |
| − | As a simple example, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s1300102.png" /> be a finite set of rational prime numbers. The rational integers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s1300103.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s1300104.png" />, relatively prime (cf. also [[Mutually-prime numbers|Mutually-prime numbers]]), such that the set of prime divisors of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s1300105.png" /> (possibly empty) is contained in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s1300106.png" /> are the so-called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s1300108.png" />-integers (corresponding to the specific set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s1300109.png" />). Clearly, this is a subring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001010.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001011.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001012.png" /> denote the group of units of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001013.png" />, i.e. the group of multiplicatively invertible elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001014.png" /> (the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001016.png" />-units). Clearly, these are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001017.png" /> and the rational numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001018.png" /> in the prime decomposition of which only prime numbers from the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001019.png" /> appear.
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. |
| | | | |
| − | These notions can be defined in a more sophisticated way, the advantage of which is that it can be generalized to the more general case of a [[Number field|number field]]. For this the notion of absolute value on a number field is needed. Unfortunately, there is no general agreement on the definition of this notion. Below, this "absolute value" is taken in the sense of a metric as in [[#References|[a1]]], Chap. 1, Sect. 4; Chap. 4, Sect. 4; equivalently, an absolute value is a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001020.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001021.png" /> is a fixed, conveniently chosen positive real number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001022.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001023.png" /> is a valuation, as defined and used in [[#References|[a2]]], Chap. 1, § 2; Chap. 3 § 1, (cf. also [[Valuation|Valuation]], which gives a slightly different definition).
| + | Out of 59 formulas, 58 were replaced by TEX code.--> |
| | | | |
| − | In the special case above, every rational prime number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001024.png" /> gives rise to a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001026.png" />-adic absolute value and all possible absolute values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001027.png" /> are (up to topological equivalence) the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001028.png" />-adic ones (non-Archimedean), denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001029.png" />, and the usual absolute value (Archimedean), denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001030.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001031.png" /> denote the set of absolute values (more precisely, the set of equivalence classes of absolute values (i.e. places) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001032.png" />; cf. also [[Place of a field|Place of a field]]). Thus, every element of this set is of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001033.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001034.png" /> is either a rational prime number or the symbol <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001035.png" />. One now modifies the definition of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001036.png" /> above as the subset of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001037.png" /> containing the absolute values (i.e. places) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001038.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001039.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001040.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001041.png" />.
| + | {{TEX|semi-auto}}{{TEX|partial}} |
| | + | As a simple example, let $S = \{ p _ { 1 } , \dots , p _ { n } \}$ be a finite set of rational prime numbers. The rational integers $a / b$, $a , b \in \mathbf{Z}$, relatively prime (cf. also [[Mutually-prime numbers|Mutually-prime numbers]]), such that the set of prime divisors of $b$ (possibly empty) is contained in $S$ are the so-called $S$-integers (corresponding to the specific set $S$). Clearly, this is a subring $R_S$ of $\mathbf{Q}$. Let $R _ { S } ^ { * }$ denote the group of units of $R_S$, i.e. the group of multiplicatively invertible elements of $R_S$ (the $S$-units). Clearly, these are $\pm$ and the rational numbers $x$ in the prime decomposition of which only prime numbers from the set $S$ appear. |
| | | | |
| − | Consider now the more general situation, where a number field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001042.png" /> is taken in place of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001043.png" /> and its ring of integers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001044.png" /> is taken in place of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001045.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001046.png" /> be the set of absolute values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001047.png" /> (more precisely, the set of equivalence classes of absolute values, i.e. places, of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001048.png" />). These are divided into two categories, namely, the non-Archimedean ones, which are in one-to-one correspondence with the prime ideals (or, what is essentially the same, with the prime divisors) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001049.png" /> and the Archimedean ones, which are in one-to-one correspondence with the isomorphic embeddings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001050.png" /> (complex-conjugate embeddings giving rise to the same absolute value). As before, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001051.png" /> be a finite subset of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001052.png" /> containing all Archimedean valuations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001053.png" />. Then, the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001054.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001055.png" />-integers and the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001056.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001057.png" />-units are defined exactly as in the case of rational numbers (see the definitions above), where now <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001058.png" /> is replaced by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001059.png" />.
| + | These notions can be defined in a more sophisticated way, the advantage of which is that it can be generalized to the more general case of a [[Number field|number field]]. For this the notion of absolute value on a number field is needed. Unfortunately, there is no general agreement on the definition of this notion. Below, this "absolute value" is taken in the sense of a metric as in [[#References|[a1]]], Chap. 1, Sect. 4; Chap. 4, Sect. 4; equivalently, an absolute value is a function $\rho ^ { v(.) }$, where $\rho$ is a fixed, conveniently chosen positive real number $< 1$ and $v$ is a valuation, as defined and used in [[#References|[a2]]], Chap. 1, § 2; Chap. 3 § 1, (cf. also [[Valuation|Valuation]], which gives a slightly different definition). |
| | | | |
| − | Many interesting problems concerning the solution of [[Diophantine equations|Diophantine equations]] are reduced to questions about <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001060.png" />-integers of "particularly simple form" (e.g. linear forms in two unknown parameters), which are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001061.png" />-units, and then results are obtained by applying a variety of relevant results on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001062.png" />-integers and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001063.png" />-units.
| + | In the special case above, every rational prime number $p$ gives rise to a $p$-adic absolute value and all possible absolute values of $\mathbf{Q}$ are (up to topological equivalence) the $p$-adic ones (non-Archimedean), denoted by $|.|_p$, and the usual absolute value (Archimedean), denoted by $|.| _ { \infty }$. Let $M _ { \operatorname{Q} }$ denote the set of absolute values (more precisely, the set of equivalence classes of absolute values (i.e. places) of $\mathbf{Q}$; cf. also [[Place of a field|Place of a field]]). Thus, every element of this set is of the form $|.| v$, where $v$ is either a rational prime number or the symbol $\infty$. One now modifies the definition of the set $S$ above as the subset of $M _ { \operatorname{Q} }$ containing the absolute values (i.e. places) $|.| v$, where $v \in \{ p _ { 1 } , \dots , p _ { n } , \infty \}$. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130010/s13001040.png"/> and $R _ { S } ^ { * } = \{ x \in \mathbf{Q} : | x | _ { v } = 1 , \forall | \cdot | _ { v } \notin S \}$. |
| | + | |
| | + | Consider now the more general situation, where a number field $K$ is taken in place of $\mathbf{Q}$ and its ring of integers $\mathcal{O} _ { K }$ is taken in place of $\bf Z$. Let $M _ { K }$ be the set of absolute values of $K$ (more precisely, the set of equivalence classes of absolute values, i.e. places, of $K$). These are divided into two categories, namely, the non-Archimedean ones, which are in one-to-one correspondence with the prime ideals (or, what is essentially the same, with the prime divisors) of $K$ and the Archimedean ones, which are in one-to-one correspondence with the isomorphic embeddings $K \hookrightarrow \bf C$ (complex-conjugate embeddings giving rise to the same absolute value). As before, let $S$ be a finite subset of $M _ { K }$ containing all Archimedean valuations of $K$. Then, the set $R_S$ of $S$-integers and the set $R _ { S } ^ { * }$ of $S$-units are defined exactly as in the case of rational numbers (see the definitions above), where now $\mathbf{Q}$ is replaced by $K$. |
| | + | |
| | + | Many interesting problems concerning the solution of [[Diophantine equations|Diophantine equations]] are reduced to questions about $S$-integers of "particularly simple form" (e.g. linear forms in two unknown parameters), which are $S$-units, and then results are obtained by applying a variety of relevant results on $S$-integers and $S$-units. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> Z.I. Borevich, I.R. Shafarevich, "Number Theory" , Acad. Press (1966) (In Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Narkiewicz, "Elementary and analytic theory of algebraic numbers" , PWN/Springer (1990)</TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> Z.I. Borevich, I.R. Shafarevich, "Number Theory" , Acad. Press (1966) (In Russian)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> W. Narkiewicz, "Elementary and analytic theory of algebraic numbers" , PWN/Springer (1990)</td></tr></table> |
As a simple example, let $S = \{ p _ { 1 } , \dots , p _ { n } \}$ be a finite set of rational prime numbers. The rational integers $a / b$, $a , b \in \mathbf{Z}$, relatively prime (cf. also Mutually-prime numbers), such that the set of prime divisors of $b$ (possibly empty) is contained in $S$ are the so-called $S$-integers (corresponding to the specific set $S$). Clearly, this is a subring $R_S$ of $\mathbf{Q}$. Let $R _ { S } ^ { * }$ denote the group of units of $R_S$, i.e. the group of multiplicatively invertible elements of $R_S$ (the $S$-units). Clearly, these are $\pm$ and the rational numbers $x$ in the prime decomposition of which only prime numbers from the set $S$ appear.
These notions can be defined in a more sophisticated way, the advantage of which is that it can be generalized to the more general case of a number field. For this the notion of absolute value on a number field is needed. Unfortunately, there is no general agreement on the definition of this notion. Below, this "absolute value" is taken in the sense of a metric as in [a1], Chap. 1, Sect. 4; Chap. 4, Sect. 4; equivalently, an absolute value is a function $\rho ^ { v(.) }$, where $\rho$ is a fixed, conveniently chosen positive real number $< 1$ and $v$ is a valuation, as defined and used in [a2], Chap. 1, § 2; Chap. 3 § 1, (cf. also Valuation, which gives a slightly different definition).
In the special case above, every rational prime number $p$ gives rise to a $p$-adic absolute value and all possible absolute values of $\mathbf{Q}$ are (up to topological equivalence) the $p$-adic ones (non-Archimedean), denoted by $|.|_p$, and the usual absolute value (Archimedean), denoted by $|.| _ { \infty }$. Let $M _ { \operatorname{Q} }$ denote the set of absolute values (more precisely, the set of equivalence classes of absolute values (i.e. places) of $\mathbf{Q}$; cf. also Place of a field). Thus, every element of this set is of the form $|.| v$, where $v$ is either a rational prime number or the symbol $\infty$. One now modifies the definition of the set $S$ above as the subset of $M _ { \operatorname{Q} }$ containing the absolute values (i.e. places) $|.| v$, where $v \in \{ p _ { 1 } , \dots , p _ { n } , \infty \}$. Then 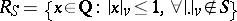 and $R _ { S } ^ { * } = \{ x \in \mathbf{Q} : | x | _ { v } = 1 , \forall | \cdot | _ { v } \notin S \}$.
and $R _ { S } ^ { * } = \{ x \in \mathbf{Q} : | x | _ { v } = 1 , \forall | \cdot | _ { v } \notin S \}$.
Consider now the more general situation, where a number field $K$ is taken in place of $\mathbf{Q}$ and its ring of integers $\mathcal{O} _ { K }$ is taken in place of $\bf Z$. Let $M _ { K }$ be the set of absolute values of $K$ (more precisely, the set of equivalence classes of absolute values, i.e. places, of $K$). These are divided into two categories, namely, the non-Archimedean ones, which are in one-to-one correspondence with the prime ideals (or, what is essentially the same, with the prime divisors) of $K$ and the Archimedean ones, which are in one-to-one correspondence with the isomorphic embeddings $K \hookrightarrow \bf C$ (complex-conjugate embeddings giving rise to the same absolute value). As before, let $S$ be a finite subset of $M _ { K }$ containing all Archimedean valuations of $K$. Then, the set $R_S$ of $S$-integers and the set $R _ { S } ^ { * }$ of $S$-units are defined exactly as in the case of rational numbers (see the definitions above), where now $\mathbf{Q}$ is replaced by $K$.
Many interesting problems concerning the solution of Diophantine equations are reduced to questions about $S$-integers of "particularly simple form" (e.g. linear forms in two unknown parameters), which are $S$-units, and then results are obtained by applying a variety of relevant results on $S$-integers and $S$-units.
References
| [a1] | Z.I. Borevich, I.R. Shafarevich, "Number Theory" , Acad. Press (1966) (In Russian) |
| [a2] | W. Narkiewicz, "Elementary and analytic theory of algebraic numbers" , PWN/Springer (1990) |
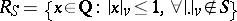 and $R _ { S } ^ { * } = \{ x \in \mathbf{Q} : | x | _ { v } = 1 , \forall | \cdot | _ { v } \notin S \}$.
and $R _ { S } ^ { * } = \{ x \in \mathbf{Q} : | x | _ { v } = 1 , \forall | \cdot | _ { v } \notin S \}$.