|
|
| Line 1: |
Line 1: |
| − | A theory of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i1300901.png" />-extensions introduced by K. Iwasawa [[#References|[a8]]]. Its motivation has been a strong analogy between number fields and curves over finite fields. One of the most fruitful results in this theory is the Iwasawa main conjecture, which has been proved for totally real number fields [[#References|[a19]]]. The conjecture is considered as an analogue of Weil's result that the characteristic polynomial of the Frobenius automorphism acting on the Jacobian of a curve over a finite field is the essential part of the zeta-function of the curve. A lot of methods and ideas developed in the theory appeared to be widely applicable and have given rise to major advances, for example, results on the [[Birch–Swinnerton-Dyer conjecture]] [[#References|[a3]]], [[#References|[a6]]], [[#References|[a16]]], [[#References|[a22]]] and on Fermat's last theorem [[#References|[a20]]] (cf. also [[Fermat last theorem|Fermat last theorem]]). For details and generalizations of Iwasawa theory, see [[#References|[a10]]], [[#References|[a7]]], [[#References|[a12]]], [[#References|[a18]]].
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. |
| | | | |
| − | ==<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i1300902.png" />-extension of a number field.==
| + | Out of 239 formulas, 233 were replaced by TEX code.--> |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i1300903.png" /> be a prime number and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i1300904.png" /> be a finite extension of the rational number field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i1300905.png" />. A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i1300907.png" />-extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i1300908.png" /> is an extension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i1300909.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009010.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009011.png" /> is the additive group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009012.png" />-adic integers. Then there is a sequence of fields
| |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009013.png" /></td> </tr></table>
| + | {{TEX|semi-auto}}{{TEX|partial}} |
| | + | A theory of $\mathbf{Z} _ { p }$-extensions introduced by K. Iwasawa [[#References|[a8]]]. Its motivation has been a strong analogy between number fields and curves over finite fields. One of the most fruitful results in this theory is the Iwasawa main conjecture, which has been proved for totally real number fields [[#References|[a19]]]. The conjecture is considered as an analogue of Weil's result that the characteristic polynomial of the Frobenius automorphism acting on the Jacobian of a curve over a finite field is the essential part of the zeta-function of the curve. A lot of methods and ideas developed in the theory appeared to be widely applicable and have given rise to major advances, for example, results on the [[Birch–Swinnerton-Dyer conjecture]] [[#References|[a3]]], [[#References|[a6]]], [[#References|[a16]]], [[#References|[a22]]] and on Fermat's last theorem [[#References|[a20]]] (cf. also [[Fermat last theorem|Fermat last theorem]]). For details and generalizations of Iwasawa theory, see [[#References|[a10]]], [[#References|[a7]]], [[#References|[a12]]], [[#References|[a18]]]. |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009014.png" /> is a cyclic extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009015.png" /> of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009016.png" />. [[Class field theory|Class field theory]] shows that there are at least <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009017.png" /> independent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009018.png" />-extensions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009019.png" /> (cf. below, the section Leopoldt conjecture). Every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009020.png" /> has at least one <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009021.png" />-extension, namely the cyclotomic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009022.png" />-extension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009023.png" />. It is obtained by letting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009024.png" /> be an appropriate subfield of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009025.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009026.png" /> is the group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009027.png" />th roots of unity.
| + | ==$\mathbf{Z} _ { p }$-extension of a number field.== |
| | + | Let $p$ be a prime number and let $k$ be a finite extension of the rational number field $\mathbf{Q}$. A $\mathbf{Z} _ { p }$-extension of $k$ is an extension $K / k$ with $\operatorname{Gal}( K / k ) \cong \mathbf{Z} _ { p }$, where $\mathbf{Z} _ { p }$ is the additive group of $p$-adic integers. Then there is a sequence of fields |
| | + | |
| | + | \begin{equation*} k = k _ { 0 } \subset k _ { 1 } \subset \ldots \subset k _ { n } \subset \ldots \subset K = \bigcup _ { n \geq 0 } k _ { n }, \end{equation*} |
| | + | |
| | + | where $k _ { n }$ is a cyclic extension of $k$ of degree $p ^ { n }$. [[Class field theory|Class field theory]] shows that there are at least $1 + r _ { 2 } ( k )$ independent $\mathbf{Z} _ { p }$-extensions of $k$ (cf. below, the section Leopoldt conjecture). Every $k$ has at least one $\mathbf{Z} _ { p }$-extension, namely the cyclotomic $\mathbf{Z} _ { p }$-extension $k _ { \infty }$. It is obtained by letting $k _ { \infty }$ be an appropriate subfield of $\cup _ { n \geq 0 } k ( \mu _ { p ^ n} )$, where $\mu _ { \mathcal{m} }$ is the group of $m$th roots of unity. |
| | | | |
| | ==Leopoldt conjecture.== | | ==Leopoldt conjecture.== |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009028.png" /> be the group of units of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009029.png" /> which are congruent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009030.png" /> modulo every prime ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009031.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009032.png" /> lying above <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009033.png" />. By Dirichlet's unit theorem, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009034.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009035.png" /> (resp. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009036.png" />) is the number of embeddings of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009037.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009038.png" /> (resp. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009039.png" />). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009040.png" /> be the group of local units of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009041.png" /> congruent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009042.png" /> modulo <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009043.png" />. There is an embedding <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009044.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009045.png" />). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009046.png" /> denote the topological closure of the image. It is Leopoldt's conjecture that the equality | + | Let $E _ { 1 } ( k )$ be the group of units of $k$ which are congruent to $1$ modulo every prime ideal $\mathfrak{p}$ of $k$ lying above $p$. By Dirichlet's unit theorem, $\operatorname{rank}_{\mathbf{Z}} E _ { 1 } ( k ) = r _ { 1 } ( k ) + r _ { 2 } ( k ) - 1$, where $r _ { 1 } ( k )$ (resp. $2 r_ 2 ( k )$) is the number of embeddings of $k$ in $\mathbf{R}$ (resp. $\mathbf{C}$). Let $U _ { 1 , \mathfrak p }$ be the group of local units of $k _ { \mathfrak p }$ congruent to $1$ modulo $\mathfrak{p}$. There is an embedding $E _ { 1 } ( k ) \rightarrow \prod _ { \mathfrak{p} | p } U _ { 1 , \mathfrak{p} }$ ($\varepsilon \mapsto ( \varepsilon , \ldots , \varepsilon )$). Let $\overline{E} _ { 1 } ( k )$ denote the topological closure of the image. It is Leopoldt's conjecture that the equality |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009047.png" /></td> </tr></table>
| + | \begin{equation*} \operatorname{ rank }_Z E _ { 1 } ( k ) = \operatorname { rank } _ { Z p } \overline{E} _ { 1 } ( k ) \end{equation*} |
| | | | |
| − | holds for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009048.png" />. A. Brumer [[#References|[a1]]] proved the conjecture for Abelian extensions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009049.png" /> (or an imaginary quadratic field). Put <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009050.png" />. Then class field theory shows that there are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009051.png" /> independent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009052.png" />-extensions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009053.png" />. | + | holds for every $k$. A. Brumer [[#References|[a1]]] proved the conjecture for Abelian extensions $k / \mathbf{Q}$ (or an imaginary quadratic field). Put $\delta _ { p } ( k ) = \operatorname { rank } _ {\bf Z } \overline{E} _ { 1 } ( k ) - \operatorname { rank } _ { {\bf Z} _ { p } } E _ { 1 } ( k ) \geq 0$. Then class field theory shows that there are $1 + r _ { 2 } ( k ) + \delta _ { p } ( k )$ independent $\mathbf{Z} _ { p }$-extensions of $k$. |
| | | | |
| | ==Iwasawa module.== | | ==Iwasawa module.== |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009054.png" /> be the integer ring of a finite extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009055.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009056.png" /> a uniformizer of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009057.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009058.png" /> be a compact Abelian group isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009059.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009060.png" />, where the inverse limit is taken with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009061.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009062.png" />) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009063.png" />. Fix a topological generator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009064.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009065.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009066.png" /> be the ring of formal power series in an indeterminate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009067.png" /> with coefficients in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009068.png" />. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009069.png" /> is called a distinguished polynomial if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009070.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009071.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009072.png" />. The prime ideals of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009073.png" /> are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009074.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009075.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009076.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009077.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009078.png" /> is distinguished and irreducible. The classification of compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009079.png" />-modules in [[#References|[a8]]] was simplified by J.-P. Serre, who pointed out that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009080.png" /> is topologically isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009081.png" />, hence each compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009082.png" />-module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009083.png" /> admits the unique structure of a compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009084.png" />-module such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009085.png" /> for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009086.png" />. Finitely-generated <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009087.png" />-modules are called Iwasawa modules. They are classified as follows: for an Iwasawa module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009088.png" />, there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009089.png" />-homomorphism | + | Let $\mathcal{O}$ be the integer ring of a finite extension of $\mathbf{Q} _ { p }$ and $\pi$ a uniformizer of $\mathcal{O}$. Let $\Gamma$ be a compact Abelian group isomorphic to $\mathbf{Z} _ { p }$ and $R = {\cal O} [ [ \Gamma ] ] = \text { varprojlim } {\cal O} [ \Gamma / \Gamma ^ { p ^ { n } } ]$, where the inverse limit is taken with respect to $\Gamma / \Gamma ^ { p^m } \rightarrow \Gamma / \Gamma ^ { p ^n }$ ($\gamma \operatorname{mod} \Gamma ^ { p^m } \mapsto \gamma \operatorname { mod } \Gamma ^ { p ^ { n } }$) for $m \geq n$. Fix a topological generator $\gamma$ of $\Gamma$. Let $\Lambda = \mathcal{O} [ [ T ] ]$ be the ring of formal power series in an indeterminate $T$ with coefficients in $\mathcal{O}$. $P ( T ) \in \mathcal{O} [ T ]$ is called a distinguished polynomial if $P ( T ) = T ^ { n } + a _ { n - 1 } T ^ { n - 1 } + \ldots + a _ { 0 }$ with $a _ { i } \in ( \pi )$ for $0 \leq i \leq n - 1$. The prime ideals of $\Lambda$ are $0$, $( \pi , T )$, $( \pi )$, $( P ( T ) )$, where $P ( T )$ is distinguished and irreducible. The classification of compact $R$-modules in [[#References|[a8]]] was simplified by J.-P. Serre, who pointed out that $R$ is topologically isomorphic to $\Lambda$, hence each compact $R$-module $X$ admits the unique structure of a compact $\Lambda$-module such that $( 1 + T ) x = \gamma . x$ for every $x \in X$. Finitely-generated $\Lambda$-modules are called Iwasawa modules. They are classified as follows: for an Iwasawa module $X$, there is a $\Lambda$-homomorphism |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009090.png" /></td> </tr></table>
| + | \begin{equation*} \varphi : X \rightarrow \Lambda ^ { r } \bigoplus\bigoplus _ { i = 1 } ^ { s } \Lambda / (\, f _ { i } ( T ) ^ { l _i} ) \bigoplus \bigoplus _ { j = 1 } ^ { t } \Lambda / ( \pi ^ { m _ { j } } ) \end{equation*} |
| | | | |
| − | with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009091.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009092.png" /> finite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009093.png" />-modules, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009094.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009095.png" /> is distinguished and irreducible. For a torsion <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009096.png" />-module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009097.png" />, i.e., <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009098.png" />, one defines | + | with $\operatorname{Ker} \varphi$ and $\operatorname {Coker} \varphi$ finite $\Lambda$-modules, where $r , s , l _ { i } , t , m_ { j } \in \mathbf{Z}_{ \geq 0}$ and $f _ { i } ( T )$ is distinguished and irreducible. For a torsion $\Lambda$-module $X$, i.e., $r = 0$, one defines |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009099.png" /></td> </tr></table>
| + | \begin{equation*} \operatorname { char } ( X ) = \prod _ { i = 1 } ^ { s } f _ { i } ( T ) ^ { l _ { i } } \prod _ { j = 1 } ^ { t } \pi ^ { m _ { j } }, \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090100.png" /></td> </tr></table>
| + | \begin{equation*} \lambda ( X ) = \sum _ { i = 1 } ^ { s } \operatorname { deg } ( f _ { i } ( T ) ^ { l _ { i } } ) , \ \mu ( X ) = \sum _ { j = 1 } ^ { t } m _ { j }. \end{equation*} |
| | | | |
| | ==Iwasawa invariant.== | | ==Iwasawa invariant.== |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090101.png" /> be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090102.png" />-extension. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090103.png" /> denote the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090104.png" />-Sylow subgroup of the ideal class group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090105.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090106.png" /> be the order of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090107.png" />. Iwasawa [[#References|[a8]]] proved that there exist integers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090108.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090109.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090110.png" /> such that | + | Let $K / k$ be a $\mathbf{Z} _ { p }$-extension. Let $A _ { n } ( k )$ denote the $p$-Sylow subgroup of the ideal class group of $k _ { n }$. Let $p ^ { e_n}$ be the order of $A _ { n } ( k )$. Iwasawa [[#References|[a8]]] proved that there exist integers $\lambda _ { p } ( K / k ) \geq 0$, $\mu _ { p } ( K / k ) \geq 0$ and $\nu _ { p } ( K / k )$ such that |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090111.png" /></td> </tr></table>
| + | \begin{equation*} e _ { n } = \lambda _ { p } ( K / k ) n + \mu _ { p } ( K / k ) p ^ { n } + \nu _ { p } ( K / k ) \end{equation*} |
| | | | |
| − | for all sufficiently large <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090112.png" />. The invariants <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090113.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090114.png" /> can be obtained from the Iwasawa module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090115.png" />, where the inverse limit is taken with respect to the relative norm mappings. Put <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090116.png" />. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090117.png" /> is a compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090118.png" />-module in a natural way. One fixes a topological generator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090119.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090120.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090121.png" /> is considered as a compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090122.png" />-module (cf. the section on Iwasawa module above). Since <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090123.png" /> is finite, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090124.png" /> is a finitely-generated torsion <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090125.png" />-module. One has that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090126.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090127.png" />. | + | for all sufficiently large $n$. The invariants $\lambda _ { p } ( K / k )$ and $\mu _ { p } ( K / k )$ can be obtained from the Iwasawa module $X = \text { varprojlim } A _ { n } ( k )$, where the inverse limit is taken with respect to the relative norm mappings. Put $\Gamma = \operatorname { Gal } ( K / k )$. $X$ is a compact $R = \mathbf{Z} _ { p } [ [ \Gamma ] ]$-module in a natural way. One fixes a topological generator $\gamma$ of $\Gamma$. Then $X$ is considered as a compact $\Lambda = {\bf Z} _ { p } [ [ T ] ]$-module (cf. the section on Iwasawa module above). Since $A _ { n } ( k )$ is finite, $X$ is a finitely-generated torsion $\Lambda$-module. One has that $\lambda _ { p } ( K / k ) = \lambda ( X )$ and $\mu _ { p } ( K / k ) = \mu ( X )$. |
| | | | |
| − | Iwasawa [[#References|[a9]]] constructed infinitely many non-cyclotomic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090128.png" />-extensions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090129.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090130.png" />. There are infinitely many <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090131.png" />-extensions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090132.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090133.png" />. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090134.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090135.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090136.png" /> is irregular (cf. also [[Irregular prime number|Irregular prime number]]). It is Iwasawa's conjecture that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090137.png" /> for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090138.png" />. B. Ferrero and L. Washington [[#References|[a5]]] proved this conjecture for Abelian extensions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090139.png" />. W. Sinnott [[#References|[a17]]] gave a new proof of this using the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090140.png" />-transform of a rational function. | + | Iwasawa [[#References|[a9]]] constructed infinitely many non-cyclotomic $\mathbf{Z} _ { p }$-extensions $K / k$ with $\mu _ { p } ( K / k ) > 0$. There are infinitely many $\mathbf{Z} _ { p }$-extensions $K / k$ with $\lambda _ { p } ( K / k ) > 0$. For $k = \mathbf{Q} ( \mu _ { p } )$, $\lambda _ { p } ( k _ { \infty } / k ) > 0$ if and only if $p$ is irregular (cf. also [[Irregular prime number|Irregular prime number]]). It is Iwasawa's conjecture that $\mu _ { p } ( k _ { \infty } / k ) = 0$ for every $k$. B. Ferrero and L. Washington [[#References|[a5]]] proved this conjecture for Abelian extensions $k / \mathbf{Q}$. W. Sinnott [[#References|[a17]]] gave a new proof of this using the $\Gamma$-transform of a rational function. |
| | | | |
| − | It is Greenberg's conjecture that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090141.png" /> for every totally real <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090142.png" />. For small <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090143.png" />, it was proved that there are infinitely many real quadratic fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090144.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090145.png" /> [[#References|[a14]]], [[#References|[a15]]]. There exists a lot of numerical work verifying this conjecture, mainly for real quadratic fields. | + | It is Greenberg's conjecture that $\lambda _ { p } ( k _ { \infty } / k ) = \mu _ { p } ( k _ { \infty } / k ) = 0$ for every totally real $k$. For small $p$, it was proved that there are infinitely many real quadratic fields $k$ with $\lambda _ { p } ( k _ { \infty } / k ) = \mu _ { p } ( k _ { \infty } / k ) = \nu _ { p } ( k _ { \infty } / k ) = 0$ [[#References|[a14]]], [[#References|[a15]]]. There exists a lot of numerical work verifying this conjecture, mainly for real quadratic fields. |
| | | | |
| − | It is Vandiver's conjecture that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090146.png" /> does not divide the class number of the maximal real subfield <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090147.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090148.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090149.png" />, which implies that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090150.png" />. This conjecture was verified for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090151.png" /> [[#References|[a2]]]. | + | It is Vandiver's conjecture that $p$ does not divide the class number of the maximal real subfield $k$ of ${\bf Q} ( \mu _ { p } )$ for all $p$, which implies that $\lambda _ { p } ( k _ { \infty } / k ) = \mu _ { p } ( k _ { \infty } / k ) = \nu _ { p } ( k _ { \infty } / k ) = 0$. This conjecture was verified for all $p < 12000000$ [[#References|[a2]]]. |
| | | | |
| | ==Iwasawa main conjecture.== | | ==Iwasawa main conjecture.== |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090152.png" /> be an odd prime number and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090153.png" /> a totally real number field. Fix an embedding of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090154.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090155.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090156.png" /> be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090157.png" />-adic valued Artin character for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090158.png" /> of order prime to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090159.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090160.png" /> be the extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090161.png" /> attached to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090162.png" />. Assume that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090163.png" /> is also totally real. Fix a topological generator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090164.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090165.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090166.png" /> be such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090167.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090168.png" />. | + | Let $p$ be an odd prime number and $k$ a totally real number field. Fix an embedding of $\overline{\mathbf{Q}}$ into $\overline {\bf Q } _ { p }$. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090156.png"/> be a $p$-adic valued Artin character for $k$ of order prime to $p$. Let $ { k }_\chi$ be the extension of $k$ attached to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090162.png"/>. Assume that $ { k }_\chi$ is also totally real. Fix a topological generator $\gamma$ of $\Gamma = \operatorname { Gal } ( k _ { \chi , \infty } / k _ { \chi } ) \cong \operatorname { Gal } ( k _ { \chi } ( \mu _ { p } \infty ) / k _ { \chi } ( \mu _ { p } ) )$ and let $u \in \mathbf{Z} _ { p } ^ { \times }$ be such that $\zeta ^ { \gamma } = \zeta ^ { u }$ for all $\zeta \in \mu _ { p ^ \infty}$. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090169.png" /> be the Teichmüller character | + | Let $\omega$ be the Teichmüller character |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090170.png" /></td> </tr></table>
| + | \begin{equation*} \omega : \operatorname { Gal } ( k ( \mu _ { p } ) / k ) \rightarrow {\bf Z} _ { p } ^ { \times } ( \omega ( a ) \equiv a \operatorname { mod } p ) \end{equation*} |
| | | | |
| − | and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090171.png" /> be the classical <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090173.png" />-function for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090174.png" />. Following T. Kubota and H.W. Leopoldt [[#References|[a11]]], P. Deligne and K. Ribet [[#References|[a4]]] proved the existence of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090177.png" />-adic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090178.png" />-function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090179.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090180.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090181.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090182.png" /> is trivial) satisfying the following interpolation property: | + | and let $L ( s , \chi )$ be the classical $L$-function for $k$. Following T. Kubota and H.W. Leopoldt [[#References|[a11]]], P. Deligne and K. Ribet [[#References|[a4]]] proved the existence of a $p$-adic $L$-function $L _ { p } ( s , \chi )$ on $s \in \mathbf{Z} _ { p }$ ($s \neq 1$ if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090182.png"/> is trivial) satisfying the following interpolation property: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090183.png" /></td> </tr></table>
| + | \begin{equation*} L _ { p } ( 1 - n , \chi ) = L ( 1 - n , \chi \omega ^ { - n } ) \prod _ { {\frak p} | p } ( 1 - \chi \omega ^ { - n } ( {\frak p} ) N {\frak p} ^ { n - 1 } ) \end{equation*} |
| | | | |
| − | for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090184.png" />. There exists a unique power series <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090185.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090186.png" /> (if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090187.png" /> is trivial, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090188.png" />), where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090189.png" /> is the ring generated over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090190.png" /> by the values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090191.png" />. By the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090193.png" />-adic Weierstrass preparation theorem (cf. also [[Weierstrass theorem|Weierstrass theorem]]), one can write <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090194.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090195.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090196.png" /> is a distinguished polynomial, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090197.png" /> is a uniformizer of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090198.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090199.png" /> is a unit power series. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090200.png" /> be such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090201.png" /> (if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090202.png" /> is trivial, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090203.png" />). One can similarly define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090204.png" /> and a distinguished polynomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090205.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090206.png" />. | + | for $n \geq 1$. There exists a unique power series $G _ { \chi } ( T ) \in \mathbf{Z} _ { p } [ \chi ] [ [ T ] ]$ such that $L _ { p } ( 1 - s , \chi ) = G _ { \chi } ( u ^ { s } - 1 )$ (if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090187.png"/> is trivial, $L _ { p } ( 1 - s , \chi ) = G _ { \chi } ( u ^ { s } - 1 ) / ( u ^ { s } - 1 )$), where $\mathbf{Z} _ { p } [ \chi ]$ is the ring generated over $\mathbf{Z} _ { p }$ by the values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090191.png"/>. By the $p$-adic Weierstrass preparation theorem (cf. also [[Weierstrass theorem|Weierstrass theorem]]), one can write $G _ { \chi } ( T ) = \pi ^ { \mu_\chi } g _ { \chi } ( T ) u _ { \chi } ( T )$, where $\mu _ { \chi } \in \mathbf{Z} _ { \geq 0 }$, $g _ { \chi } ( T )$ is a distinguished polynomial, $\pi$ is a uniformizer of $\mathbf{Z} _ { p } [ \chi ]$, and $u _ { \chi } ( T )$ is a unit power series. Let $G _ { \chi } ^ { * } ( T ) \in \mathbf{Z} _ { p } [ \chi ] [ [ T ] ]$ be such that $L _ { p } ( s , \chi ) = G _ { \chi } ^ { * } ( u ^ { s } - 1 )$ (if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090202.png"/> is trivial, $L _ { p } ( s , \chi ) = G _ { \chi } ^ { * } ( u ^ { s } - 1 ) / ( u ^ { s } - u )$). One can similarly define $\mu _ { \chi } ^ { * } = \mu _ { \chi }$ and a distinguished polynomial $g _ { \chi } ^ { * } ( T )$ for $G _ { \chi } ^ { * } ( T )$. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090207.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090208.png" /> be the maximal unramified Abelian <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090210.png" />-extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090211.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090212.png" /> the maximal Abelian <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090214.png" />-extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090215.png" />, which are both unramified outside the primes above <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090216.png" />. By class field theory, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090217.png" />. Extend <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090218.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090219.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090220.png" /> acts on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090221.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090222.png" />. Put <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090223.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090224.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090225.png" />, | + | Let $k ^ { \prime } = k _ { \chi } ( \mu _ { p } )$, let $L ( k ^ { \prime } )$ be the maximal unramified Abelian $p$-extension of $k _ { \infty } ^ { \prime }$ and $M ( k ^ { \prime } )$ the maximal Abelian $p$-extension of $k _ { \infty } ^ { \prime }$, which are both unramified outside the primes above $p$. By class field theory, $\operatorname {Gal}( L ( k ^ { \prime } ) / k _ { \infty } ^ { \prime } ) \cong \text { varprojlim } A _ { n } ( k ^ { \prime } )$. Extend $g \in \operatorname { Gal } ( k _ { \infty } ^ { \prime } / k )$ to $\tilde{g} \in \operatorname { Gal } ( L ( k ^ { \prime } ) / k )$. Then $g$ acts on $x \in \operatorname { Gal } ( L ( k ^ { \prime } ) / k _ { \infty } ^ { \prime } )$ by $g.x = \tilde{g} x \tilde{g} ^ { - 1 }$. Put $X = \operatorname { Gal } ( L ( k ^ { \prime } ) / k _ { \infty } ^ { \prime } ) \otimes \mathbf{Z} _ { p } [ \chi ]$ and $Y = \operatorname { Gal } ( M ( k ^ { \prime } ) / k _ { \infty } ^ { \prime } ) \otimes \mathbf{Z} _ { p } [ \chi ]$. Let $\Delta = \text { Gal } ( k _ { \infty } ^ { \prime } / k _ { \infty } ) \cong \text { Gal } ( k ^ { \prime } / k )$, |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090226.png" /></td> </tr></table>
| + | \begin{equation*} X ^ { \omega \chi ^ { - 1 }} = \{ x \in X : \delta . x = \omega \chi ^ { - 1 } ( \delta ) x \text{ for } \delta \in \Delta \}, \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090227.png" /></td> </tr></table>
| + | \begin{equation*} Y ^ { \chi } = \{ y \in Y : \delta \cdot y = \chi ( \delta ) y \, \text { for } \delta \in \Delta \}. \end{equation*} |
| | | | |
| − | Then one can regard <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090228.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090229.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090230.png" />-modules. | + | Then one can regard $X ^ { \omega } \chi ^ { - 1 }$ and $Y^{\chi}$ as $\Lambda = \mathbf{Z} _ { p } [ \chi ] [ [ T ] ]$-modules. |
| | | | |
| | Following [[#References|[a13]]], A. Wiles proved the following equality, i.e., the Iwasawa main conjecture for totally real fields: | | Following [[#References|[a13]]], A. Wiles proved the following equality, i.e., the Iwasawa main conjecture for totally real fields: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090231.png" /></td> </tr></table>
| + | \begin{equation*} \operatorname{char}( X ^ { \omega \chi ^ { - 1 }} ) = \pi ^ { \mu _ { \chi } ^ { * } } g _ { \chi } ^ { * } ( T ). \end{equation*} |
| | | | |
| | This equality is equivalent to | | This equality is equivalent to |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090232.png" /></td> </tr></table>
| + | \begin{equation*} \operatorname { char } ( Y ^ { \chi } ) = \pi ^ { \mu _{\chi}} g _ { \chi } ( T ). \end{equation*} |
| | | | |
| | The proof uses delicate techniques from modular forms, especially Hida's theory of modular forms, to construct unramified extensions. | | The proof uses delicate techniques from modular forms, especially Hida's theory of modular forms, to construct unramified extensions. |
| | | | |
| − | Following Stickelberger's theorem, F. Thaine and V. Kolyvagin invented techniques for constructing relations in ideal class groups. These methods, which use Gauss sums (cyclotomic units or elliptic units) satisfying properties known as the Euler system, have given elementary proofs of the Iwasawa main conjecture for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090233.png" /> [[#References|[a12]]], [[#References|[a21]]]. | + | Following Stickelberger's theorem, F. Thaine and V. Kolyvagin invented techniques for constructing relations in ideal class groups. These methods, which use Gauss sums (cyclotomic units or elliptic units) satisfying properties known as the Euler system, have given elementary proofs of the Iwasawa main conjecture for $k = \mathbf{Q}$ [[#References|[a12]]], [[#References|[a21]]]. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Brumer, "On the units of algebraic number fields" ''Mathematika'' , '''14''' (1967) pp. 121–124 {{MR|0220694}} {{ZBL|0171.01105}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Buhler, R. Crandall, R. Ernvall, T. Metsänkylä, M.A. Shokrollahi, "Irregular primes and cyclotomic invariants to 12 million" ''J. Symbolic Comput.'' , '''31''' (2001) pp. 89–96 {{MR|1806208}} {{ZBL|1001.11061}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Coates, A. Wiles, "On the conjecture of Birch and Swinnerton-Dyer" ''Invent. Math.'' , '''39''' (1977) pp. 223–251 {{MR|0463176}} {{ZBL|0359.14009}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> P. Deligne, K. Ribet, "Values of abelian <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090234.png" />-functions at negative integers over totally real fields" ''Invent. Math.'' , '''59''' (1980) pp. 227–286 {{MR|579702}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> B. Ferrero, L. Washington, "The Iwasawa invariant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090235.png" /> vanishes for abelian number fields" ''Ann. of Math.'' , '''109''' (1979) pp. 377–395 {{MR|528968}} {{ZBL|0443.12001}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> R. Greenberg, "On the Birch and Swinnerton-Dyer conjecture" ''Invent. Math.'' , '''72''' (1983) pp. 241–265 {{MR|0700770}} {{ZBL|0546.14015}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> K. Iwasawa, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090236.png" />-extensions of algebraic number fields" ''Ann. of Math.'' , '''98''' (1973) pp. 246–326 {{MR|349627}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> K. Iwasawa, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090237.png" />-extensions of algebraic number fields" ''Bull. Amer. Math. Soc.'' , '''65''' (1959) pp. 183–226 {{MR|124316}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> K. Iwasawa, "On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090238.png" />-invariants of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090239.png" />-extensions" , ''Number Theory, Algebraic Geometry and Commutative Algebra, in honor of Y. Akizuki'' , Kinokuniya (1973) pp. 1–11 {{MR|357371}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> J. Coates, R. Greenberg, B. Mazur, I. Satake, "Algebraic Number Theory—In Honor of K. Iwasawa" , ''Adv. Studies in Pure Math.'' , '''17''' , Acad. Press (1989) {{MR|}} {{ZBL|0721.00006}} </TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> T. Kubota, H.W. Leopoldt, "Eine <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090240.png" />-adische Theorie der Zetawerte, I. Einführung der <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090241.png" />-adischen Dirichletschen <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090242.png" />-Funktionen" ''J. Reine Angew. Math.'' , '''214/215''' (1964) pp. 328–339 {{MR|0163900}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> S. Lang, "Cyclotomic fields I—II" , ''Graduate Texts in Math.'' , '''121''' , Springer (1990) (with an appendix by K. Rubin)</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> B. Mazur, A. Wiles, "Class fields of abelian extensions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090243.png" />" ''Invent. Math.'' , '''76''' (1984) pp. 179–330 {{MR|0742853}} {{ZBL|0545.12005}} </TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> J. Nakagawa, K. Horie, "Elliptic curves with no rational points" ''Proc. Amer. Math. Soc.'' , '''104''' (1988) pp. 20–24 {{MR|0958035}} {{ZBL|0663.14023}} </TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> K. Ono, "Indivisibility of class numbers of real quadratic fields" ''Compositio Math.'' , '''119''' (1999) pp. 1–11 {{MR|1711515}} {{ZBL|1002.11080}} </TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> K. Rubin, "Tate–Shafarevich groups and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090244.png" />-functions of elliptic curves with complex multiplication" ''Invent. Math.'' , '''89''' (1987) pp. 527–560 {{MR|0903383}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> W. Sinnott, "On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090245.png" />-invariant of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i130090246.png" />-transform of a rational function" ''Invent. Math.'' , '''75''' (1984) pp. 273–282 {{MR|732547}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> L. Washington, "Introduction to cyclotomic fields" , ''Graduate Texts in Math.'' , '''83''' , Springer (1997) (Edition: Second) {{MR|1421575}} {{ZBL|0966.11047}} </TD></TR><TR><TD valign="top">[a19]</TD> <TD valign="top"> A. Wiles, "The Iwasawa conjecture for totally real fields" ''Ann. of Math.'' , '''131''' (1990) pp. 493–540 {{MR|1053488}} {{ZBL|0719.11071}} </TD></TR><TR><TD valign="top">[a20]</TD> <TD valign="top"> A. Wiles, "Modular elliptic curves and Fermat's last theorem" ''Ann. of Math.'' , '''141''' (1995) pp. 443–551</TD></TR><TR><TD valign="top">[a21]</TD> <TD valign="top"> K. Rubin, "The "main conjectures" of Iwasawa theory for imaginary quadratic fields" ''Invent. Math.'' , '''103''' (1991) pp. 25–68 {{MR|1157660}} {{MR|1143122}} {{MR|1136002}} {{MR|1124840}} {{MR|1110401}} {{MR|1079839}} {{MR|1034427}} {{ZBL|0946.60500}} {{ZBL|0825.62832}} {{ZBL|0773.55002}} {{ZBL|0743.76074}} {{ZBL|0741.11028}} {{ZBL|0737.11030}} </TD></TR><TR><TD valign="top">[a22]</TD> <TD valign="top"> K. Rubin, "Euler systems and modular elliptic curves" , ''Galois Representations in Arithmetic Algebraic Geometry (Durham, 1996)'' , ''London Math. Soc. Lecture Notes'' , '''284''' , Cambridge Univ. Press (1998) pp. 351–367 {{MR|1696493}} {{ZBL|0952.11016}} </TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> A. Brumer, "On the units of algebraic number fields" ''Mathematika'' , '''14''' (1967) pp. 121–124 {{MR|0220694}} {{ZBL|0171.01105}} </td></tr><tr><td valign="top">[a2]</td> <td valign="top"> J. Buhler, R. Crandall, R. Ernvall, T. Metsänkylä, M.A. Shokrollahi, "Irregular primes and cyclotomic invariants to 12 million" ''J. Symbolic Comput.'' , '''31''' (2001) pp. 89–96 {{MR|1806208}} {{ZBL|1001.11061}} </td></tr><tr><td valign="top">[a3]</td> <td valign="top"> J. Coates, A. Wiles, "On the conjecture of Birch and Swinnerton-Dyer" ''Invent. Math.'' , '''39''' (1977) pp. 223–251 {{MR|0463176}} {{ZBL|0359.14009}} </td></tr><tr><td valign="top">[a4]</td> <td valign="top"> P. Deligne, K. Ribet, "Values of abelian $L$-functions at negative integers over totally real fields" ''Invent. Math.'' , '''59''' (1980) pp. 227–286 {{MR|579702}} {{ZBL|}} </td></tr><tr><td valign="top">[a5]</td> <td valign="top"> B. Ferrero, L. Washington, "The Iwasawa invariant $\mu _ { p }$ vanishes for abelian number fields" ''Ann. of Math.'' , '''109''' (1979) pp. 377–395 {{MR|528968}} {{ZBL|0443.12001}} </td></tr><tr><td valign="top">[a6]</td> <td valign="top"> R. Greenberg, "On the Birch and Swinnerton-Dyer conjecture" ''Invent. Math.'' , '''72''' (1983) pp. 241–265 {{MR|0700770}} {{ZBL|0546.14015}} </td></tr><tr><td valign="top">[a7]</td> <td valign="top"> K. Iwasawa, "On $\mathbf{Z}_l$-extensions of algebraic number fields" ''Ann. of Math.'' , '''98''' (1973) pp. 246–326 {{MR|349627}} {{ZBL|}} </td></tr><tr><td valign="top">[a8]</td> <td valign="top"> K. Iwasawa, "On $\Gamma$-extensions of algebraic number fields" ''Bull. Amer. Math. Soc.'' , '''65''' (1959) pp. 183–226 {{MR|124316}} {{ZBL|}} </td></tr><tr><td valign="top">[a9]</td> <td valign="top"> K. Iwasawa, "On the $\mu$-invariants of $\mathbf{Z}_l$-extensions" , ''Number Theory, Algebraic Geometry and Commutative Algebra, in honor of Y. Akizuki'' , Kinokuniya (1973) pp. 1–11 {{MR|357371}} {{ZBL|}} </td></tr><tr><td valign="top">[a10]</td> <td valign="top"> J. Coates, R. Greenberg, B. Mazur, I. Satake, "Algebraic Number Theory—In Honor of K. Iwasawa" , ''Adv. Studies in Pure Math.'' , '''17''' , Acad. Press (1989) {{MR|}} {{ZBL|0721.00006}} </td></tr><tr><td valign="top">[a11]</td> <td valign="top"> T. Kubota, H.W. Leopoldt, "Eine $p$-adische Theorie der Zetawerte, I. Einführung der $p$-adischen Dirichletschen $L$-Funktionen" ''J. Reine Angew. Math.'' , '''214/215''' (1964) pp. 328–339 {{MR|0163900}} {{ZBL|}} </td></tr><tr><td valign="top">[a12]</td> <td valign="top"> S. Lang, "Cyclotomic fields I—II" , ''Graduate Texts in Math.'' , '''121''' , Springer (1990) (with an appendix by K. Rubin)</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> B. Mazur, A. Wiles, "Class fields of abelian extensions of $\mathbf{Q}$" ''Invent. Math.'' , '''76''' (1984) pp. 179–330 {{MR|0742853}} {{ZBL|0545.12005}} </td></tr><tr><td valign="top">[a14]</td> <td valign="top"> J. Nakagawa, K. Horie, "Elliptic curves with no rational points" ''Proc. Amer. Math. Soc.'' , '''104''' (1988) pp. 20–24 {{MR|0958035}} {{ZBL|0663.14023}} </td></tr><tr><td valign="top">[a15]</td> <td valign="top"> K. Ono, "Indivisibility of class numbers of real quadratic fields" ''Compositio Math.'' , '''119''' (1999) pp. 1–11 {{MR|1711515}} {{ZBL|1002.11080}} </td></tr><tr><td valign="top">[a16]</td> <td valign="top"> K. Rubin, "Tate–Shafarevich groups and $L$-functions of elliptic curves with complex multiplication" ''Invent. Math.'' , '''89''' (1987) pp. 527–560 {{MR|0903383}} {{ZBL|}} </td></tr><tr><td valign="top">[a17]</td> <td valign="top"> W. Sinnott, "On the $\mu$-invariant of the $\Gamma$-transform of a rational function" ''Invent. Math.'' , '''75''' (1984) pp. 273–282 {{MR|732547}} {{ZBL|}} </td></tr><tr><td valign="top">[a18]</td> <td valign="top"> L. Washington, "Introduction to cyclotomic fields" , ''Graduate Texts in Math.'' , '''83''' , Springer (1997) (Edition: Second) {{MR|1421575}} {{ZBL|0966.11047}} </td></tr><tr><td valign="top">[a19]</td> <td valign="top"> A. Wiles, "The Iwasawa conjecture for totally real fields" ''Ann. of Math.'' , '''131''' (1990) pp. 493–540 {{MR|1053488}} {{ZBL|0719.11071}} </td></tr><tr><td valign="top">[a20]</td> <td valign="top"> A. Wiles, "Modular elliptic curves and Fermat's last theorem" ''Ann. of Math.'' , '''141''' (1995) pp. 443–551</td></tr><tr><td valign="top">[a21]</td> <td valign="top"> K. Rubin, "The "main conjectures" of Iwasawa theory for imaginary quadratic fields" ''Invent. Math.'' , '''103''' (1991) pp. 25–68 {{MR|1157660}} {{MR|1143122}} {{MR|1136002}} {{MR|1124840}} {{MR|1110401}} {{MR|1079839}} {{MR|1034427}} {{ZBL|0946.60500}} {{ZBL|0825.62832}} {{ZBL|0773.55002}} {{ZBL|0743.76074}} {{ZBL|0741.11028}} {{ZBL|0737.11030}} </td></tr><tr><td valign="top">[a22]</td> <td valign="top"> K. Rubin, "Euler systems and modular elliptic curves" , ''Galois Representations in Arithmetic Algebraic Geometry (Durham, 1996)'' , ''London Math. Soc. Lecture Notes'' , '''284''' , Cambridge Univ. Press (1998) pp. 351–367 {{MR|1696493}} {{ZBL|0952.11016}} </td></tr></table> |
A theory of $\mathbf{Z} _ { p }$-extensions introduced by K. Iwasawa [a8]. Its motivation has been a strong analogy between number fields and curves over finite fields. One of the most fruitful results in this theory is the Iwasawa main conjecture, which has been proved for totally real number fields [a19]. The conjecture is considered as an analogue of Weil's result that the characteristic polynomial of the Frobenius automorphism acting on the Jacobian of a curve over a finite field is the essential part of the zeta-function of the curve. A lot of methods and ideas developed in the theory appeared to be widely applicable and have given rise to major advances, for example, results on the Birch–Swinnerton-Dyer conjecture [a3], [a6], [a16], [a22] and on Fermat's last theorem [a20] (cf. also Fermat last theorem). For details and generalizations of Iwasawa theory, see [a10], [a7], [a12], [a18].
$\mathbf{Z} _ { p }$-extension of a number field.
Let $p$ be a prime number and let $k$ be a finite extension of the rational number field $\mathbf{Q}$. A $\mathbf{Z} _ { p }$-extension of $k$ is an extension $K / k$ with $\operatorname{Gal}( K / k ) \cong \mathbf{Z} _ { p }$, where $\mathbf{Z} _ { p }$ is the additive group of $p$-adic integers. Then there is a sequence of fields
\begin{equation*} k = k _ { 0 } \subset k _ { 1 } \subset \ldots \subset k _ { n } \subset \ldots \subset K = \bigcup _ { n \geq 0 } k _ { n }, \end{equation*}
where $k _ { n }$ is a cyclic extension of $k$ of degree $p ^ { n }$. Class field theory shows that there are at least $1 + r _ { 2 } ( k )$ independent $\mathbf{Z} _ { p }$-extensions of $k$ (cf. below, the section Leopoldt conjecture). Every $k$ has at least one $\mathbf{Z} _ { p }$-extension, namely the cyclotomic $\mathbf{Z} _ { p }$-extension $k _ { \infty }$. It is obtained by letting $k _ { \infty }$ be an appropriate subfield of $\cup _ { n \geq 0 } k ( \mu _ { p ^ n} )$, where $\mu _ { \mathcal{m} }$ is the group of $m$th roots of unity.
Leopoldt conjecture.
Let $E _ { 1 } ( k )$ be the group of units of $k$ which are congruent to $1$ modulo every prime ideal $\mathfrak{p}$ of $k$ lying above $p$. By Dirichlet's unit theorem, $\operatorname{rank}_{\mathbf{Z}} E _ { 1 } ( k ) = r _ { 1 } ( k ) + r _ { 2 } ( k ) - 1$, where $r _ { 1 } ( k )$ (resp. $2 r_ 2 ( k )$) is the number of embeddings of $k$ in $\mathbf{R}$ (resp. $\mathbf{C}$). Let $U _ { 1 , \mathfrak p }$ be the group of local units of $k _ { \mathfrak p }$ congruent to $1$ modulo $\mathfrak{p}$. There is an embedding $E _ { 1 } ( k ) \rightarrow \prod _ { \mathfrak{p} | p } U _ { 1 , \mathfrak{p} }$ ($\varepsilon \mapsto ( \varepsilon , \ldots , \varepsilon )$). Let $\overline{E} _ { 1 } ( k )$ denote the topological closure of the image. It is Leopoldt's conjecture that the equality
\begin{equation*} \operatorname{ rank }_Z E _ { 1 } ( k ) = \operatorname { rank } _ { Z p } \overline{E} _ { 1 } ( k ) \end{equation*}
holds for every $k$. A. Brumer [a1] proved the conjecture for Abelian extensions $k / \mathbf{Q}$ (or an imaginary quadratic field). Put $\delta _ { p } ( k ) = \operatorname { rank } _ {\bf Z } \overline{E} _ { 1 } ( k ) - \operatorname { rank } _ { {\bf Z} _ { p } } E _ { 1 } ( k ) \geq 0$. Then class field theory shows that there are $1 + r _ { 2 } ( k ) + \delta _ { p } ( k )$ independent $\mathbf{Z} _ { p }$-extensions of $k$.
Iwasawa module.
Let $\mathcal{O}$ be the integer ring of a finite extension of $\mathbf{Q} _ { p }$ and $\pi$ a uniformizer of $\mathcal{O}$. Let $\Gamma$ be a compact Abelian group isomorphic to $\mathbf{Z} _ { p }$ and $R = {\cal O} [ [ \Gamma ] ] = \text { varprojlim } {\cal O} [ \Gamma / \Gamma ^ { p ^ { n } } ]$, where the inverse limit is taken with respect to $\Gamma / \Gamma ^ { p^m } \rightarrow \Gamma / \Gamma ^ { p ^n }$ ($\gamma \operatorname{mod} \Gamma ^ { p^m } \mapsto \gamma \operatorname { mod } \Gamma ^ { p ^ { n } }$) for $m \geq n$. Fix a topological generator $\gamma$ of $\Gamma$. Let $\Lambda = \mathcal{O} [ [ T ] ]$ be the ring of formal power series in an indeterminate $T$ with coefficients in $\mathcal{O}$. $P ( T ) \in \mathcal{O} [ T ]$ is called a distinguished polynomial if $P ( T ) = T ^ { n } + a _ { n - 1 } T ^ { n - 1 } + \ldots + a _ { 0 }$ with $a _ { i } \in ( \pi )$ for $0 \leq i \leq n - 1$. The prime ideals of $\Lambda$ are $0$, $( \pi , T )$, $( \pi )$, $( P ( T ) )$, where $P ( T )$ is distinguished and irreducible. The classification of compact $R$-modules in [a8] was simplified by J.-P. Serre, who pointed out that $R$ is topologically isomorphic to $\Lambda$, hence each compact $R$-module $X$ admits the unique structure of a compact $\Lambda$-module such that $( 1 + T ) x = \gamma . x$ for every $x \in X$. Finitely-generated $\Lambda$-modules are called Iwasawa modules. They are classified as follows: for an Iwasawa module $X$, there is a $\Lambda$-homomorphism
\begin{equation*} \varphi : X \rightarrow \Lambda ^ { r } \bigoplus\bigoplus _ { i = 1 } ^ { s } \Lambda / (\, f _ { i } ( T ) ^ { l _i} ) \bigoplus \bigoplus _ { j = 1 } ^ { t } \Lambda / ( \pi ^ { m _ { j } } ) \end{equation*}
with $\operatorname{Ker} \varphi$ and $\operatorname {Coker} \varphi$ finite $\Lambda$-modules, where $r , s , l _ { i } , t , m_ { j } \in \mathbf{Z}_{ \geq 0}$ and $f _ { i } ( T )$ is distinguished and irreducible. For a torsion $\Lambda$-module $X$, i.e., $r = 0$, one defines
\begin{equation*} \operatorname { char } ( X ) = \prod _ { i = 1 } ^ { s } f _ { i } ( T ) ^ { l _ { i } } \prod _ { j = 1 } ^ { t } \pi ^ { m _ { j } }, \end{equation*}
\begin{equation*} \lambda ( X ) = \sum _ { i = 1 } ^ { s } \operatorname { deg } ( f _ { i } ( T ) ^ { l _ { i } } ) , \ \mu ( X ) = \sum _ { j = 1 } ^ { t } m _ { j }. \end{equation*}
Iwasawa invariant.
Let $K / k$ be a $\mathbf{Z} _ { p }$-extension. Let $A _ { n } ( k )$ denote the $p$-Sylow subgroup of the ideal class group of $k _ { n }$. Let $p ^ { e_n}$ be the order of $A _ { n } ( k )$. Iwasawa [a8] proved that there exist integers $\lambda _ { p } ( K / k ) \geq 0$, $\mu _ { p } ( K / k ) \geq 0$ and $\nu _ { p } ( K / k )$ such that
\begin{equation*} e _ { n } = \lambda _ { p } ( K / k ) n + \mu _ { p } ( K / k ) p ^ { n } + \nu _ { p } ( K / k ) \end{equation*}
for all sufficiently large $n$. The invariants $\lambda _ { p } ( K / k )$ and $\mu _ { p } ( K / k )$ can be obtained from the Iwasawa module $X = \text { varprojlim } A _ { n } ( k )$, where the inverse limit is taken with respect to the relative norm mappings. Put $\Gamma = \operatorname { Gal } ( K / k )$. $X$ is a compact $R = \mathbf{Z} _ { p } [ [ \Gamma ] ]$-module in a natural way. One fixes a topological generator $\gamma$ of $\Gamma$. Then $X$ is considered as a compact $\Lambda = {\bf Z} _ { p } [ [ T ] ]$-module (cf. the section on Iwasawa module above). Since $A _ { n } ( k )$ is finite, $X$ is a finitely-generated torsion $\Lambda$-module. One has that $\lambda _ { p } ( K / k ) = \lambda ( X )$ and $\mu _ { p } ( K / k ) = \mu ( X )$.
Iwasawa [a9] constructed infinitely many non-cyclotomic $\mathbf{Z} _ { p }$-extensions $K / k$ with $\mu _ { p } ( K / k ) > 0$. There are infinitely many $\mathbf{Z} _ { p }$-extensions $K / k$ with $\lambda _ { p } ( K / k ) > 0$. For $k = \mathbf{Q} ( \mu _ { p } )$, $\lambda _ { p } ( k _ { \infty } / k ) > 0$ if and only if $p$ is irregular (cf. also Irregular prime number). It is Iwasawa's conjecture that $\mu _ { p } ( k _ { \infty } / k ) = 0$ for every $k$. B. Ferrero and L. Washington [a5] proved this conjecture for Abelian extensions $k / \mathbf{Q}$. W. Sinnott [a17] gave a new proof of this using the $\Gamma$-transform of a rational function.
It is Greenberg's conjecture that $\lambda _ { p } ( k _ { \infty } / k ) = \mu _ { p } ( k _ { \infty } / k ) = 0$ for every totally real $k$. For small $p$, it was proved that there are infinitely many real quadratic fields $k$ with $\lambda _ { p } ( k _ { \infty } / k ) = \mu _ { p } ( k _ { \infty } / k ) = \nu _ { p } ( k _ { \infty } / k ) = 0$ [a14], [a15]. There exists a lot of numerical work verifying this conjecture, mainly for real quadratic fields.
It is Vandiver's conjecture that $p$ does not divide the class number of the maximal real subfield $k$ of ${\bf Q} ( \mu _ { p } )$ for all $p$, which implies that $\lambda _ { p } ( k _ { \infty } / k ) = \mu _ { p } ( k _ { \infty } / k ) = \nu _ { p } ( k _ { \infty } / k ) = 0$. This conjecture was verified for all $p < 12000000$ [a2].
Iwasawa main conjecture.
Let $p$ be an odd prime number and $k$ a totally real number field. Fix an embedding of $\overline{\mathbf{Q}}$ into $\overline {\bf Q } _ { p }$. Let 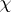 be a $p$-adic valued Artin character for $k$ of order prime to $p$. Let $ { k }_\chi$ be the extension of $k$ attached to
be a $p$-adic valued Artin character for $k$ of order prime to $p$. Let $ { k }_\chi$ be the extension of $k$ attached to 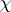 . Assume that $ { k }_\chi$ is also totally real. Fix a topological generator $\gamma$ of $\Gamma = \operatorname { Gal } ( k _ { \chi , \infty } / k _ { \chi } ) \cong \operatorname { Gal } ( k _ { \chi } ( \mu _ { p } \infty ) / k _ { \chi } ( \mu _ { p } ) )$ and let $u \in \mathbf{Z} _ { p } ^ { \times }$ be such that $\zeta ^ { \gamma } = \zeta ^ { u }$ for all $\zeta \in \mu _ { p ^ \infty}$.
. Assume that $ { k }_\chi$ is also totally real. Fix a topological generator $\gamma$ of $\Gamma = \operatorname { Gal } ( k _ { \chi , \infty } / k _ { \chi } ) \cong \operatorname { Gal } ( k _ { \chi } ( \mu _ { p } \infty ) / k _ { \chi } ( \mu _ { p } ) )$ and let $u \in \mathbf{Z} _ { p } ^ { \times }$ be such that $\zeta ^ { \gamma } = \zeta ^ { u }$ for all $\zeta \in \mu _ { p ^ \infty}$.
Let $\omega$ be the Teichmüller character
\begin{equation*} \omega : \operatorname { Gal } ( k ( \mu _ { p } ) / k ) \rightarrow {\bf Z} _ { p } ^ { \times } ( \omega ( a ) \equiv a \operatorname { mod } p ) \end{equation*}
and let $L ( s , \chi )$ be the classical $L$-function for $k$. Following T. Kubota and H.W. Leopoldt [a11], P. Deligne and K. Ribet [a4] proved the existence of a $p$-adic $L$-function $L _ { p } ( s , \chi )$ on $s \in \mathbf{Z} _ { p }$ ($s \neq 1$ if 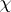 is trivial) satisfying the following interpolation property:
is trivial) satisfying the following interpolation property:
\begin{equation*} L _ { p } ( 1 - n , \chi ) = L ( 1 - n , \chi \omega ^ { - n } ) \prod _ { {\frak p} | p } ( 1 - \chi \omega ^ { - n } ( {\frak p} ) N {\frak p} ^ { n - 1 } ) \end{equation*}
for $n \geq 1$. There exists a unique power series $G _ { \chi } ( T ) \in \mathbf{Z} _ { p } [ \chi ] [ [ T ] ]$ such that $L _ { p } ( 1 - s , \chi ) = G _ { \chi } ( u ^ { s } - 1 )$ (if 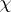 is trivial, $L _ { p } ( 1 - s , \chi ) = G _ { \chi } ( u ^ { s } - 1 ) / ( u ^ { s } - 1 )$), where $\mathbf{Z} _ { p } [ \chi ]$ is the ring generated over $\mathbf{Z} _ { p }$ by the values of
is trivial, $L _ { p } ( 1 - s , \chi ) = G _ { \chi } ( u ^ { s } - 1 ) / ( u ^ { s } - 1 )$), where $\mathbf{Z} _ { p } [ \chi ]$ is the ring generated over $\mathbf{Z} _ { p }$ by the values of 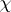 . By the $p$-adic Weierstrass preparation theorem (cf. also Weierstrass theorem), one can write $G _ { \chi } ( T ) = \pi ^ { \mu_\chi } g _ { \chi } ( T ) u _ { \chi } ( T )$, where $\mu _ { \chi } \in \mathbf{Z} _ { \geq 0 }$, $g _ { \chi } ( T )$ is a distinguished polynomial, $\pi$ is a uniformizer of $\mathbf{Z} _ { p } [ \chi ]$, and $u _ { \chi } ( T )$ is a unit power series. Let $G _ { \chi } ^ { * } ( T ) \in \mathbf{Z} _ { p } [ \chi ] [ [ T ] ]$ be such that $L _ { p } ( s , \chi ) = G _ { \chi } ^ { * } ( u ^ { s } - 1 )$ (if
. By the $p$-adic Weierstrass preparation theorem (cf. also Weierstrass theorem), one can write $G _ { \chi } ( T ) = \pi ^ { \mu_\chi } g _ { \chi } ( T ) u _ { \chi } ( T )$, where $\mu _ { \chi } \in \mathbf{Z} _ { \geq 0 }$, $g _ { \chi } ( T )$ is a distinguished polynomial, $\pi$ is a uniformizer of $\mathbf{Z} _ { p } [ \chi ]$, and $u _ { \chi } ( T )$ is a unit power series. Let $G _ { \chi } ^ { * } ( T ) \in \mathbf{Z} _ { p } [ \chi ] [ [ T ] ]$ be such that $L _ { p } ( s , \chi ) = G _ { \chi } ^ { * } ( u ^ { s } - 1 )$ (if 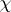 is trivial, $L _ { p } ( s , \chi ) = G _ { \chi } ^ { * } ( u ^ { s } - 1 ) / ( u ^ { s } - u )$). One can similarly define $\mu _ { \chi } ^ { * } = \mu _ { \chi }$ and a distinguished polynomial $g _ { \chi } ^ { * } ( T )$ for $G _ { \chi } ^ { * } ( T )$.
is trivial, $L _ { p } ( s , \chi ) = G _ { \chi } ^ { * } ( u ^ { s } - 1 ) / ( u ^ { s } - u )$). One can similarly define $\mu _ { \chi } ^ { * } = \mu _ { \chi }$ and a distinguished polynomial $g _ { \chi } ^ { * } ( T )$ for $G _ { \chi } ^ { * } ( T )$.
Let $k ^ { \prime } = k _ { \chi } ( \mu _ { p } )$, let $L ( k ^ { \prime } )$ be the maximal unramified Abelian $p$-extension of $k _ { \infty } ^ { \prime }$ and $M ( k ^ { \prime } )$ the maximal Abelian $p$-extension of $k _ { \infty } ^ { \prime }$, which are both unramified outside the primes above $p$. By class field theory, $\operatorname {Gal}( L ( k ^ { \prime } ) / k _ { \infty } ^ { \prime } ) \cong \text { varprojlim } A _ { n } ( k ^ { \prime } )$. Extend $g \in \operatorname { Gal } ( k _ { \infty } ^ { \prime } / k )$ to $\tilde{g} \in \operatorname { Gal } ( L ( k ^ { \prime } ) / k )$. Then $g$ acts on $x \in \operatorname { Gal } ( L ( k ^ { \prime } ) / k _ { \infty } ^ { \prime } )$ by $g.x = \tilde{g} x \tilde{g} ^ { - 1 }$. Put $X = \operatorname { Gal } ( L ( k ^ { \prime } ) / k _ { \infty } ^ { \prime } ) \otimes \mathbf{Z} _ { p } [ \chi ]$ and $Y = \operatorname { Gal } ( M ( k ^ { \prime } ) / k _ { \infty } ^ { \prime } ) \otimes \mathbf{Z} _ { p } [ \chi ]$. Let $\Delta = \text { Gal } ( k _ { \infty } ^ { \prime } / k _ { \infty } ) \cong \text { Gal } ( k ^ { \prime } / k )$,
\begin{equation*} X ^ { \omega \chi ^ { - 1 }} = \{ x \in X : \delta . x = \omega \chi ^ { - 1 } ( \delta ) x \text{ for } \delta \in \Delta \}, \end{equation*}
\begin{equation*} Y ^ { \chi } = \{ y \in Y : \delta \cdot y = \chi ( \delta ) y \, \text { for } \delta \in \Delta \}. \end{equation*}
Then one can regard $X ^ { \omega } \chi ^ { - 1 }$ and $Y^{\chi}$ as $\Lambda = \mathbf{Z} _ { p } [ \chi ] [ [ T ] ]$-modules.
Following [a13], A. Wiles proved the following equality, i.e., the Iwasawa main conjecture for totally real fields:
\begin{equation*} \operatorname{char}( X ^ { \omega \chi ^ { - 1 }} ) = \pi ^ { \mu _ { \chi } ^ { * } } g _ { \chi } ^ { * } ( T ). \end{equation*}
This equality is equivalent to
\begin{equation*} \operatorname { char } ( Y ^ { \chi } ) = \pi ^ { \mu _{\chi}} g _ { \chi } ( T ). \end{equation*}
The proof uses delicate techniques from modular forms, especially Hida's theory of modular forms, to construct unramified extensions.
Following Stickelberger's theorem, F. Thaine and V. Kolyvagin invented techniques for constructing relations in ideal class groups. These methods, which use Gauss sums (cyclotomic units or elliptic units) satisfying properties known as the Euler system, have given elementary proofs of the Iwasawa main conjecture for $k = \mathbf{Q}$ [a12], [a21].
References
| [a1] | A. Brumer, "On the units of algebraic number fields" Mathematika , 14 (1967) pp. 121–124 MR0220694 Zbl 0171.01105 |
| [a2] | J. Buhler, R. Crandall, R. Ernvall, T. Metsänkylä, M.A. Shokrollahi, "Irregular primes and cyclotomic invariants to 12 million" J. Symbolic Comput. , 31 (2001) pp. 89–96 MR1806208 Zbl 1001.11061 |
| [a3] | J. Coates, A. Wiles, "On the conjecture of Birch and Swinnerton-Dyer" Invent. Math. , 39 (1977) pp. 223–251 MR0463176 Zbl 0359.14009 |
| [a4] | P. Deligne, K. Ribet, "Values of abelian $L$-functions at negative integers over totally real fields" Invent. Math. , 59 (1980) pp. 227–286 MR579702 |
| [a5] | B. Ferrero, L. Washington, "The Iwasawa invariant $\mu _ { p }$ vanishes for abelian number fields" Ann. of Math. , 109 (1979) pp. 377–395 MR528968 Zbl 0443.12001 |
| [a6] | R. Greenberg, "On the Birch and Swinnerton-Dyer conjecture" Invent. Math. , 72 (1983) pp. 241–265 MR0700770 Zbl 0546.14015 |
| [a7] | K. Iwasawa, "On $\mathbf{Z}_l$-extensions of algebraic number fields" Ann. of Math. , 98 (1973) pp. 246–326 MR349627 |
| [a8] | K. Iwasawa, "On $\Gamma$-extensions of algebraic number fields" Bull. Amer. Math. Soc. , 65 (1959) pp. 183–226 MR124316 |
| [a9] | K. Iwasawa, "On the $\mu$-invariants of $\mathbf{Z}_l$-extensions" , Number Theory, Algebraic Geometry and Commutative Algebra, in honor of Y. Akizuki , Kinokuniya (1973) pp. 1–11 MR357371 |
| [a10] | J. Coates, R. Greenberg, B. Mazur, I. Satake, "Algebraic Number Theory—In Honor of K. Iwasawa" , Adv. Studies in Pure Math. , 17 , Acad. Press (1989) Zbl 0721.00006 |
| [a11] | T. Kubota, H.W. Leopoldt, "Eine $p$-adische Theorie der Zetawerte, I. Einführung der $p$-adischen Dirichletschen $L$-Funktionen" J. Reine Angew. Math. , 214/215 (1964) pp. 328–339 MR0163900 |
| [a12] | S. Lang, "Cyclotomic fields I—II" , Graduate Texts in Math. , 121 , Springer (1990) (with an appendix by K. Rubin) |
| [a13] | B. Mazur, A. Wiles, "Class fields of abelian extensions of $\mathbf{Q}$" Invent. Math. , 76 (1984) pp. 179–330 MR0742853 Zbl 0545.12005 |
| [a14] | J. Nakagawa, K. Horie, "Elliptic curves with no rational points" Proc. Amer. Math. Soc. , 104 (1988) pp. 20–24 MR0958035 Zbl 0663.14023 |
| [a15] | K. Ono, "Indivisibility of class numbers of real quadratic fields" Compositio Math. , 119 (1999) pp. 1–11 MR1711515 Zbl 1002.11080 |
| [a16] | K. Rubin, "Tate–Shafarevich groups and $L$-functions of elliptic curves with complex multiplication" Invent. Math. , 89 (1987) pp. 527–560 MR0903383 |
| [a17] | W. Sinnott, "On the $\mu$-invariant of the $\Gamma$-transform of a rational function" Invent. Math. , 75 (1984) pp. 273–282 MR732547 |
| [a18] | L. Washington, "Introduction to cyclotomic fields" , Graduate Texts in Math. , 83 , Springer (1997) (Edition: Second) MR1421575 Zbl 0966.11047 |
| [a19] | A. Wiles, "The Iwasawa conjecture for totally real fields" Ann. of Math. , 131 (1990) pp. 493–540 MR1053488 Zbl 0719.11071 |
| [a20] | A. Wiles, "Modular elliptic curves and Fermat's last theorem" Ann. of Math. , 141 (1995) pp. 443–551 |
| [a21] | K. Rubin, "The "main conjectures" of Iwasawa theory for imaginary quadratic fields" Invent. Math. , 103 (1991) pp. 25–68 MR1157660 MR1143122 MR1136002 MR1124840 MR1110401 MR1079839 MR1034427 Zbl 0946.60500 Zbl 0825.62832 Zbl 0773.55002 Zbl 0743.76074 Zbl 0741.11028 Zbl 0737.11030 |
| [a22] | K. Rubin, "Euler systems and modular elliptic curves" , Galois Representations in Arithmetic Algebraic Geometry (Durham, 1996) , London Math. Soc. Lecture Notes , 284 , Cambridge Univ. Press (1998) pp. 351–367 MR1696493 Zbl 0952.11016 |
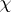 be a $p$-adic valued Artin character for $k$ of order prime to $p$. Let $ { k }_\chi$ be the extension of $k$ attached to
be a $p$-adic valued Artin character for $k$ of order prime to $p$. Let $ { k }_\chi$ be the extension of $k$ attached to 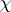 . Assume that $ { k }_\chi$ is also totally real. Fix a topological generator $\gamma$ of $\Gamma = \operatorname { Gal } ( k _ { \chi , \infty } / k _ { \chi } ) \cong \operatorname { Gal } ( k _ { \chi } ( \mu _ { p } \infty ) / k _ { \chi } ( \mu _ { p } ) )$ and let $u \in \mathbf{Z} _ { p } ^ { \times }$ be such that $\zeta ^ { \gamma } = \zeta ^ { u }$ for all $\zeta \in \mu _ { p ^ \infty}$.
. Assume that $ { k }_\chi$ is also totally real. Fix a topological generator $\gamma$ of $\Gamma = \operatorname { Gal } ( k _ { \chi , \infty } / k _ { \chi } ) \cong \operatorname { Gal } ( k _ { \chi } ( \mu _ { p } \infty ) / k _ { \chi } ( \mu _ { p } ) )$ and let $u \in \mathbf{Z} _ { p } ^ { \times }$ be such that $\zeta ^ { \gamma } = \zeta ^ { u }$ for all $\zeta \in \mu _ { p ^ \infty}$.
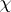 is trivial) satisfying the following interpolation property:
is trivial) satisfying the following interpolation property:
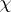 is trivial, $L _ { p } ( 1 - s , \chi ) = G _ { \chi } ( u ^ { s } - 1 ) / ( u ^ { s } - 1 )$), where $\mathbf{Z} _ { p } [ \chi ]$ is the ring generated over $\mathbf{Z} _ { p }$ by the values of
is trivial, $L _ { p } ( 1 - s , \chi ) = G _ { \chi } ( u ^ { s } - 1 ) / ( u ^ { s } - 1 )$), where $\mathbf{Z} _ { p } [ \chi ]$ is the ring generated over $\mathbf{Z} _ { p }$ by the values of 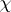 . By the $p$-adic Weierstrass preparation theorem (cf. also Weierstrass theorem), one can write $G _ { \chi } ( T ) = \pi ^ { \mu_\chi } g _ { \chi } ( T ) u _ { \chi } ( T )$, where $\mu _ { \chi } \in \mathbf{Z} _ { \geq 0 }$, $g _ { \chi } ( T )$ is a distinguished polynomial, $\pi$ is a uniformizer of $\mathbf{Z} _ { p } [ \chi ]$, and $u _ { \chi } ( T )$ is a unit power series. Let $G _ { \chi } ^ { * } ( T ) \in \mathbf{Z} _ { p } [ \chi ] [ [ T ] ]$ be such that $L _ { p } ( s , \chi ) = G _ { \chi } ^ { * } ( u ^ { s } - 1 )$ (if
. By the $p$-adic Weierstrass preparation theorem (cf. also Weierstrass theorem), one can write $G _ { \chi } ( T ) = \pi ^ { \mu_\chi } g _ { \chi } ( T ) u _ { \chi } ( T )$, where $\mu _ { \chi } \in \mathbf{Z} _ { \geq 0 }$, $g _ { \chi } ( T )$ is a distinguished polynomial, $\pi$ is a uniformizer of $\mathbf{Z} _ { p } [ \chi ]$, and $u _ { \chi } ( T )$ is a unit power series. Let $G _ { \chi } ^ { * } ( T ) \in \mathbf{Z} _ { p } [ \chi ] [ [ T ] ]$ be such that $L _ { p } ( s , \chi ) = G _ { \chi } ^ { * } ( u ^ { s } - 1 )$ (if 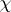 is trivial, $L _ { p } ( s , \chi ) = G _ { \chi } ^ { * } ( u ^ { s } - 1 ) / ( u ^ { s } - u )$). One can similarly define $\mu _ { \chi } ^ { * } = \mu _ { \chi }$ and a distinguished polynomial $g _ { \chi } ^ { * } ( T )$ for $G _ { \chi } ^ { * } ( T )$.
is trivial, $L _ { p } ( s , \chi ) = G _ { \chi } ^ { * } ( u ^ { s } - 1 ) / ( u ^ { s } - u )$). One can similarly define $\mu _ { \chi } ^ { * } = \mu _ { \chi }$ and a distinguished polynomial $g _ { \chi } ^ { * } ( T )$ for $G _ { \chi } ^ { * } ( T )$.