Difference between revisions of "Extended interpolation process"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 33 formulas out of 35 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 35 formulas, 33 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
An [[Interpolation process|interpolation process]] constructed from a given interpolation process by imposing additional interpolation conditions. | An [[Interpolation process|interpolation process]] constructed from a given interpolation process by imposing additional interpolation conditions. | ||
==The method of additional nodes.== | ==The method of additional nodes.== | ||
| − | The method of additional nodes was introduced by J. Szabados in [[#References|[a4]]] to approximate the derivatives of a function by means of the derivative of the Lagrange interpolating polynomial (cf. also [[Lagrange interpolation formula|Lagrange interpolation formula]]). For given interpolation nodes | + | The method of additional nodes was introduced by J. Szabados in [[#References|[a4]]] to approximate the derivatives of a function by means of the derivative of the Lagrange interpolating polynomial (cf. also [[Lagrange interpolation formula|Lagrange interpolation formula]]). For given interpolation nodes $x _ { 1 } < \ldots < x _ { m }$, the method consists in considering the interpolation process with respect to the nodes |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e120/e120270/e1202702.png"/></td> </tr></table> |
| − | where | + | where $y _ { i }$, $z_i$ are equidistant nodes between $a$ and $x_{1} $, respectively between $x _ { m }$ and $b$. |
| − | For | + | For $x _ { 1 } , \ldots , x _ { m }$ being the zeros of the Jacobi polynomial (cf. [[Jacobi polynomials|Jacobi polynomials]]) $P _ { m } ^{( \alpha , \beta )}$, $\alpha , \beta > - 1$, the [[Lebesgue constants|Lebesgue constants]] $\Lambda _ { m } ^ { \alpha , \beta }$ of the Lagrange interpolating polynomials $p _ { m } ^ { \alpha , \beta }$ have the behaviour |
| − | + | \begin{equation*} \Lambda _ { m } ^ { \alpha , \beta } \sim \operatorname { max } \{ \operatorname { log } m , m ^ { \gamma + 1 / 2 } \}, \end{equation*} | |
| − | where | + | where $\gamma = \operatorname { max } \{ \alpha , \beta \}$. Therefore, only if $\gamma \leq - 1 / 2$ will $\Lambda _ { m } ^ { \alpha , \beta }$ have the optimal behaviour $\mathcal{O} (\operatorname { log } m )$. Denoting by $\Lambda _ { m } ^ { \alpha , \beta , r , s }$ the Lebesgue constant of the extended interpolation process, one has |
| − | + | \begin{equation*} \Lambda _ { m } ^ { \alpha , \beta , r , s } \sim \operatorname { log }m \end{equation*} | |
if | if | ||
| − | + | \begin{equation*} \frac { \alpha } { 2 } + \frac { 1 } { 4 } \leq r < \frac { \alpha } { 2 } + \frac { 5 } { 4 }, \end{equation*} | |
| − | + | \begin{equation*} \frac { \beta } { 2 } + \frac { 1 } { 4 } \leq s < \frac { \beta } { 2 } + \frac { 5 } { 4 }. \end{equation*} | |
This technique has been extended to more general contexts and has led to the construction of many classes of optimal interpolation processes (see [[#References|[a1]]], [[#References|[a3]]] and the literature cited therein). These results have given important contributions to numerical [[Quadrature|quadrature]] and to collocation methods in the numerical solution of functional equations. | This technique has been extended to more general contexts and has led to the construction of many classes of optimal interpolation processes (see [[#References|[a1]]], [[#References|[a3]]] and the literature cited therein). These results have given important contributions to numerical [[Quadrature|quadrature]] and to collocation methods in the numerical solution of functional equations. | ||
==Error estimation.== | ==Error estimation.== | ||
| − | An efficient method for the practical estimation of the error of an interpolation process with respect to given nodes | + | An efficient method for the practical estimation of the error of an interpolation process with respect to given nodes $x _ { 1 } , \ldots , x _ { m }$ consists in imposing interpolation conditions at suitable additional nodes $y _ { 1 } , \ldots , y _ { n }$. In particular, a natural choice are $n = m + 1$ and nodes which interlace, |
| − | + | \begin{equation*} a \leq y _ { 1 } < x _ { 1 } < y _ { 2 } < x _ { 2 } < \ldots < x _ { m } < y _ { m + 1 } \leq b. \end{equation*} | |
| − | Let | + | Let $x _ { 1 } , \ldots , x _ { m }$ be the zeros of the [[Orthogonal polynomials|orthogonal polynomials]] $P _ { m }$ with respect to some weight function $p$. The zeros of the orthogonal polynomials $P _ { m + 1 }$ with respect to the same weight function $p$ have the interlacing property; orthogonal polynomials with respect to other weight functions have also been considered. For necessary and sufficient conditions for the convergence of the extended interpolation process, cf. [[#References|[a2]]] and the literature cited therein. The zeros $y _ { 1 } , \dots , y _ { m + 1}$ of the associated [[Stieltjes polynomials|Stieltjes polynomials]] $E _ { m + 1} $ lead to the Lagrange–Kronrod formulas, and they maximize the algebraic degree of the corresponding interpolatory quadrature formulas; the latter are the [[Gauss–Kronrod quadrature formula|Gauss–Kronrod quadrature formula]]. For the zeros of the Stieltjes polynomials, the interlacing property does not hold for general $p$, but it is known for several important weight functions including the Legendre weight (see [[Stieltjes polynomials|Stieltjes polynomials]]). Error estimation by extended interpolation is an important tool for the numerical approximation of linear functionals. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> G. Mastroianni, "Uniform convergence of derivatives of Lagrange interpolation" ''J. Comput. Appl. Math.'' , '''43''' : 2 (1992) pp. 37–51</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> G. Mastroianni, "Approximation of functions by extended Lagrange interpolation" R.V.M. Zahar (ed.) , ''Approximation and Computation'' , Birkhäuser (1995) pp. 409–420</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> P.O. Runck, P. Vértesi, "Some good point systems for derivatives of Lagrange interpolatory operators" ''Acta Math. Hung.'' , '''56''' (1990) pp. 337–342</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> J. Szabados, "On the convergence of the derivatives of projection operators" ''Analysis'' , '''7''' (1987) pp. 341–357</td></tr></table> |
Revision as of 16:57, 1 July 2020
An interpolation process constructed from a given interpolation process by imposing additional interpolation conditions.
The method of additional nodes.
The method of additional nodes was introduced by J. Szabados in [a4] to approximate the derivatives of a function by means of the derivative of the Lagrange interpolating polynomial (cf. also Lagrange interpolation formula). For given interpolation nodes $x _ { 1 } < \ldots < x _ { m }$, the method consists in considering the interpolation process with respect to the nodes
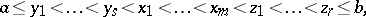 |
where $y _ { i }$, $z_i$ are equidistant nodes between $a$ and $x_{1} $, respectively between $x _ { m }$ and $b$.
For $x _ { 1 } , \ldots , x _ { m }$ being the zeros of the Jacobi polynomial (cf. Jacobi polynomials) $P _ { m } ^{( \alpha , \beta )}$, $\alpha , \beta > - 1$, the Lebesgue constants $\Lambda _ { m } ^ { \alpha , \beta }$ of the Lagrange interpolating polynomials $p _ { m } ^ { \alpha , \beta }$ have the behaviour
\begin{equation*} \Lambda _ { m } ^ { \alpha , \beta } \sim \operatorname { max } \{ \operatorname { log } m , m ^ { \gamma + 1 / 2 } \}, \end{equation*}
where $\gamma = \operatorname { max } \{ \alpha , \beta \}$. Therefore, only if $\gamma \leq - 1 / 2$ will $\Lambda _ { m } ^ { \alpha , \beta }$ have the optimal behaviour $\mathcal{O} (\operatorname { log } m )$. Denoting by $\Lambda _ { m } ^ { \alpha , \beta , r , s }$ the Lebesgue constant of the extended interpolation process, one has
\begin{equation*} \Lambda _ { m } ^ { \alpha , \beta , r , s } \sim \operatorname { log }m \end{equation*}
if
\begin{equation*} \frac { \alpha } { 2 } + \frac { 1 } { 4 } \leq r < \frac { \alpha } { 2 } + \frac { 5 } { 4 }, \end{equation*}
\begin{equation*} \frac { \beta } { 2 } + \frac { 1 } { 4 } \leq s < \frac { \beta } { 2 } + \frac { 5 } { 4 }. \end{equation*}
This technique has been extended to more general contexts and has led to the construction of many classes of optimal interpolation processes (see [a1], [a3] and the literature cited therein). These results have given important contributions to numerical quadrature and to collocation methods in the numerical solution of functional equations.
Error estimation.
An efficient method for the practical estimation of the error of an interpolation process with respect to given nodes $x _ { 1 } , \ldots , x _ { m }$ consists in imposing interpolation conditions at suitable additional nodes $y _ { 1 } , \ldots , y _ { n }$. In particular, a natural choice are $n = m + 1$ and nodes which interlace,
\begin{equation*} a \leq y _ { 1 } < x _ { 1 } < y _ { 2 } < x _ { 2 } < \ldots < x _ { m } < y _ { m + 1 } \leq b. \end{equation*}
Let $x _ { 1 } , \ldots , x _ { m }$ be the zeros of the orthogonal polynomials $P _ { m }$ with respect to some weight function $p$. The zeros of the orthogonal polynomials $P _ { m + 1 }$ with respect to the same weight function $p$ have the interlacing property; orthogonal polynomials with respect to other weight functions have also been considered. For necessary and sufficient conditions for the convergence of the extended interpolation process, cf. [a2] and the literature cited therein. The zeros $y _ { 1 } , \dots , y _ { m + 1}$ of the associated Stieltjes polynomials $E _ { m + 1} $ lead to the Lagrange–Kronrod formulas, and they maximize the algebraic degree of the corresponding interpolatory quadrature formulas; the latter are the Gauss–Kronrod quadrature formula. For the zeros of the Stieltjes polynomials, the interlacing property does not hold for general $p$, but it is known for several important weight functions including the Legendre weight (see Stieltjes polynomials). Error estimation by extended interpolation is an important tool for the numerical approximation of linear functionals.
References
| [a1] | G. Mastroianni, "Uniform convergence of derivatives of Lagrange interpolation" J. Comput. Appl. Math. , 43 : 2 (1992) pp. 37–51 |
| [a2] | G. Mastroianni, "Approximation of functions by extended Lagrange interpolation" R.V.M. Zahar (ed.) , Approximation and Computation , Birkhäuser (1995) pp. 409–420 |
| [a3] | P.O. Runck, P. Vértesi, "Some good point systems for derivatives of Lagrange interpolatory operators" Acta Math. Hung. , 56 (1990) pp. 337–342 |
| [a4] | J. Szabados, "On the convergence of the derivatives of projection operators" Analysis , 7 (1987) pp. 341–357 |
Extended interpolation process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Extended_interpolation_process&oldid=13703