Difference between revisions of "BMO-space"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 85 formulas out of 87 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 87 formulas, 85 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
''space of functions of bounded mean oscillation'' | ''space of functions of bounded mean oscillation'' | ||
| − | Functions of bounded mean oscillation were introduced by F. John and L. Nirenberg [[#References|[a8]]], [[#References|[a12]]], in connection with differential equations. The definition on | + | Functions of bounded mean oscillation were introduced by F. John and L. Nirenberg [[#References|[a8]]], [[#References|[a12]]], in connection with differential equations. The definition on ${\bf R} ^ { n }$ reads as follows: Suppose that $f$ is integrable over compact sets in ${\bf R} ^ { n }$, (i.e. $f \in L ^ { 1 _ {\operatorname{ loc }}} ( \mathbf{R} )$), and that $Q$ is any ball in ${\bf R} ^ { n }$, with volume denoted by $|Q|$. The mean of $f$ over $Q$ will be |
| − | + | \begin{equation*} f _ { Q } = \frac { 1 } { | Q | } \int _ { Q } f ( t ) d t. \end{equation*} | |
| − | By definition, | + | By definition, $f$ belongs to $\operatorname{BMO}$ if |
| − | + | \begin{equation*} \| f \| _ { * } = \operatorname { sup } _ { Q } \frac { 1 } { | Q | } \int _ { Q } | f ( t ) - f _ { Q } | d t < \infty, \end{equation*} | |
| − | where the supremum is taken over all balls | + | where the supremum is taken over all balls $Q$. Here, $\| f \|_*$ is called the $\operatorname{BMO}$-norm of $f$, and it becomes a [[Norm|norm]] on $\operatorname{BMO}$ after dividing out the constant functions. Bounded functions are in $\operatorname{BMO}$ and a $\operatorname{BMO}$-function is locally in $L _ { p } ( \mathbf{R} )$ for every $p < \infty$. Typical examples of $\operatorname{BMO}$-functions are of the form $\operatorname { log } | P |$ with $P$ a [[Polynomial|polynomial]] on ${\bf R} ^ { n }$. |
| − | The space | + | The space $\operatorname{BMO}$ is very important in modern [[Harmonic analysis|harmonic analysis]]. Taking $n = 1$, the [[Hilbert transform|Hilbert transform]] $H$, defined by $H f ( x ) = \operatorname { lim } _ { \epsilon \downarrow 0} \int _ { | t | > \epsilon } f ( x - t ) / t d t$, maps $L _ { \infty } ( \mathbf{R} )$ to $\operatorname{BMO}$ boundedly, i.e. |
| − | + | \begin{equation*} \| H f \| _ { * } \leq G \| f \| _ { \infty }. \end{equation*} | |
| − | The same is true for a large class of singular integral transformations (cf. also [[Singular integral|Singular integral]]), including Riesz transformations [[#References|[a12]]]. There is a version of the Riesz interpolation theorem (cf. also [[Riesz interpolation formula|Riesz interpolation formula]]) for analytic families of operators | + | The same is true for a large class of singular integral transformations (cf. also [[Singular integral|Singular integral]]), including Riesz transformations [[#References|[a12]]]. There is a version of the Riesz interpolation theorem (cf. also [[Riesz interpolation formula|Riesz interpolation formula]]) for analytic families of operators $\{ T _ { s } \}$, $0 \leq \operatorname { Re } s \leq 1$, which besides the $L_{2}$-boundedness assumptions on $\| T _ { i t } \|$ involves the (weak) assumption $\| T _ { 1 } + i t ( f ) \| _ { * } \leq C \| f \| _ { \infty }$ instead of the usual assumption $\| T _ { 1 + i t} ( f ) \| _ { \infty } \leq C \| f \|_\infty$, cf. [[#References|[a12]]]. However the most famous result is the Fefferman duality theorem, [[#References|[a6]]], [[#References|[a7]]], [[#References|[a12]]]. It states that the dual of $H ^ { 1 }$ is $\operatorname{BMO}$. Here, $H ^ { 1 }$ denotes the real Hardy space on ${\bf R} ^ { n }$ (cf. also [[Hardy spaces|Hardy spaces]]). The result is also valid for the usual space $H ^ { 1 }$ on the disc or the upper half-plane, with an appropriate complex multiplication on $\operatorname{BMO}$, cf. [[#References|[a5]]]. |
| − | Calderón–Zygmund operators on | + | Calderón–Zygmund operators on ${\bf R} ^ { n }$ form an important class of singular integral operators. A Calderón–Zygmund operator can be defined as a [[Linear operator|linear operator]] $T : \mathcal{D} ( \mathbf{R} ^ { n } ) \rightarrow \mathcal{D} ^ { \prime } ( \mathbf{R} ^ { n } )$ with associated [[Schwarz kernel|Schwarz kernel]] $K ( x , y )$ defined on $\Omega = \{ ( x , y ) : x , y \in \mathbf{R} ^ { n } , x \neq y \}$ with the following properties: |
| − | i) | + | i) $K$ is locally integrable on $\Omega$ and satisfies $| K ( x , y ) | = O ( | x - y | ^ { - x } )$; |
| − | ii) there exist constants | + | ii) there exist constants $C > 0$ and $0 < \gamma \leq 1$ such that for $( x , y ) \in \Omega$ and $| x ^ { \prime } - x | \leq | x - y | / 2$, |
| − | + | \begin{equation*} | K ( x - , y ) - K ( x , y ) | \leq C | x ^ { \prime } - x | ^ { \gamma } | x - y | ^ { - n - \gamma }. \end{equation*} | |
| − | Similarly, for | + | Similarly, for $( x , y ) \in \Omega$ and $| y ^ { \prime } - y | \leq | x - y | / 2$, |
| − | + | \begin{equation*} | K ( x , y ^ { \prime } ) - K ( x , y ) | \leq C | y ^ { \prime } - y | ^ { \gamma } | x - y | ^ { - n - \gamma }. \end{equation*} | |
| − | iii) | + | iii) $T$ can be extended to a bounded linear operator on $L _ { 2 } ( \mathbf{R} ^ { n } )$. |
| − | This last condition is hard to verify in general. Thus, it is an important result, known as the | + | This last condition is hard to verify in general. Thus, it is an important result, known as the $T ( 1 )$-theorem, that if i) and ii) hold, then iii) is equivalent to: $T$ is weakly bounded on $L_{2}$ and both $T ( 1 )$ and $T ^ { * } ( 1 )$ are in $\operatorname{BMO}$, cf. [[#References|[a3]]], [[#References|[a11]]], [[#References|[a12]]]. It is known that diagonal operators with respect to an orthonormal wavelet basis are of Calderón–Zygmund type. This connection with [[Wavelet analysis|wavelet analysis]] is treated in [[#References|[a11]]]. |
| − | Many of the results concerning | + | Many of the results concerning $\operatorname{BMO}$-functions have been generalized to the setting of martingales, cf. [[#References|[a9]]] (see also [[Martingale|Martingale]]). |
| − | The duality result indicates that | + | The duality result indicates that $\operatorname{BMO}$ plays a role in complex analysis as well. The class of holomorphic functions (cf. [[Analytic function|Analytic function]]) on a domain $D$ with boundary values in $\operatorname{BMO}$ is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110660/b11066077.png"/>, and is called the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110660/b11066079.png"/>-space, i.e., $= \operatorname{BMOA}= \operatorname{BMO} \cap H ^ { 2 }$. |
| − | Carleson's corona theorem [[#References|[a5]]] for the disc states that for given bounded holomorphic functions | + | Carleson's corona theorem [[#References|[a5]]] for the disc states that for given bounded holomorphic functions $f _ { 1 } , \ldots , f _ { n }$ such that $\sum _ { i } | f _ { i } | > \delta > 0$ there exist bounded holomorphic functions $g_ 1 , \ldots , g_ { n }$ such that $\sum _ { i } f _ { i } g _ { i } = 1$. So far (1996), this result could not be extended to the unit ball in $\mathbf{C}^{m}$, $m > 1$, but it can be proved if one only requires that $g_i \in \operatorname { BMOA}$, cf. [[#References|[a13]]]. |
| − | The definition of | + | The definition of $\operatorname{BMO}$ makes sense as soon as there are proper notions of integral and ball in a space. Thus, $\operatorname{BMO}$ can be defined in spaces of homogeneous type, cf. [[#References|[a1]]], [[#References|[a2]]], [[#References|[a10]]]. In the setting of several complex variables, several types of $\operatorname{BMO}$-spaces arise on the boundary of (strictly) pseudoconvex domains, depending on whether one considers the isotropic Euclidean balls or the non-isotropic balls that are natural in connection with pseudo-convexity, cf. [[#References|[a10]]]. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> R.R. Coifman, G. Weiss, "Analyse harmonique non-commutative sur certains espaces homogènes" , ''Lecture Notes in Mathematics'' , '''242''' , Springer (1971)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> R.R. Coifman, G. Weiss, "Extensions of Hardy spaces and their use in analysis" ''Bull. Amer. Math. Soc.'' , '''83''' (1977) pp. 569–643</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> G. David, J.-L. Journé, "A boundedness criterion for generalized Calderón–Zygmund operators" ''Ann. of Math.'' , '''120''' (1985) pp. 371–397</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> J. Garcia-Cuervas, J.L. Rubio de Francia, "Weighted norm inequalities and related topics" , ''Math. Stud.'' , '''116''' , North-Holland (1985)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> J. Garnett, "Bounded analytic functions" , Acad. Press (1981)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> C. Fefferman, "Characterizations of bounded mean oscillation" ''Bull. Amer. Math. Soc.'' , '''77''' (1971) pp. 587–588</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> C. Fefferman, E.M. Stein, "$H ^ { p }$ spaces of several variables" ''Acta Math.'' , '''129''' (1974) pp. 137–193</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> F. John, L. Nirenberg, "On functions of bounded mean oscillation" ''Comm. Pure Appl. Math.'' , '''14''' (1961) pp. 415–426</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> N. Kazamaki, "Continuous exponential martingales and BMO" , ''Lecture Notes in Mathematics'' , '''579''' , Springer (1994)</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> S.G. Krantz, "Geometric analysis and function spaces" , ''CBMS'' , '''81''' , Amer. Math. Soc. (1993)</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> Y. Meyer, "Ondelettes et opérateurs II. Opérateurs de Calderón–Zygmund" , ''Actual. Math.'' , Hermann (1990)</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> E.M. Stein, "Harmonic analysis: real variable methods, orthogonality, and oscillatory integrals" , ''Math. Ser.'' , '''43''' , Princeton Univ. Press (1993)</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> N.Th. Varopoulos, "BMO functions and the $\partial$ equation" ''Pacific J. Math.'' , '''71''' (1977) pp. 221–272</td></tr></table> |
Revision as of 16:57, 1 July 2020
space of functions of bounded mean oscillation
Functions of bounded mean oscillation were introduced by F. John and L. Nirenberg [a8], [a12], in connection with differential equations. The definition on ${\bf R} ^ { n }$ reads as follows: Suppose that $f$ is integrable over compact sets in ${\bf R} ^ { n }$, (i.e. $f \in L ^ { 1 _ {\operatorname{ loc }}} ( \mathbf{R} )$), and that $Q$ is any ball in ${\bf R} ^ { n }$, with volume denoted by $|Q|$. The mean of $f$ over $Q$ will be
\begin{equation*} f _ { Q } = \frac { 1 } { | Q | } \int _ { Q } f ( t ) d t. \end{equation*}
By definition, $f$ belongs to $\operatorname{BMO}$ if
\begin{equation*} \| f \| _ { * } = \operatorname { sup } _ { Q } \frac { 1 } { | Q | } \int _ { Q } | f ( t ) - f _ { Q } | d t < \infty, \end{equation*}
where the supremum is taken over all balls $Q$. Here, $\| f \|_*$ is called the $\operatorname{BMO}$-norm of $f$, and it becomes a norm on $\operatorname{BMO}$ after dividing out the constant functions. Bounded functions are in $\operatorname{BMO}$ and a $\operatorname{BMO}$-function is locally in $L _ { p } ( \mathbf{R} )$ for every $p < \infty$. Typical examples of $\operatorname{BMO}$-functions are of the form $\operatorname { log } | P |$ with $P$ a polynomial on ${\bf R} ^ { n }$.
The space $\operatorname{BMO}$ is very important in modern harmonic analysis. Taking $n = 1$, the Hilbert transform $H$, defined by $H f ( x ) = \operatorname { lim } _ { \epsilon \downarrow 0} \int _ { | t | > \epsilon } f ( x - t ) / t d t$, maps $L _ { \infty } ( \mathbf{R} )$ to $\operatorname{BMO}$ boundedly, i.e.
\begin{equation*} \| H f \| _ { * } \leq G \| f \| _ { \infty }. \end{equation*}
The same is true for a large class of singular integral transformations (cf. also Singular integral), including Riesz transformations [a12]. There is a version of the Riesz interpolation theorem (cf. also Riesz interpolation formula) for analytic families of operators $\{ T _ { s } \}$, $0 \leq \operatorname { Re } s \leq 1$, which besides the $L_{2}$-boundedness assumptions on $\| T _ { i t } \|$ involves the (weak) assumption $\| T _ { 1 } + i t ( f ) \| _ { * } \leq C \| f \| _ { \infty }$ instead of the usual assumption $\| T _ { 1 + i t} ( f ) \| _ { \infty } \leq C \| f \|_\infty$, cf. [a12]. However the most famous result is the Fefferman duality theorem, [a6], [a7], [a12]. It states that the dual of $H ^ { 1 }$ is $\operatorname{BMO}$. Here, $H ^ { 1 }$ denotes the real Hardy space on ${\bf R} ^ { n }$ (cf. also Hardy spaces). The result is also valid for the usual space $H ^ { 1 }$ on the disc or the upper half-plane, with an appropriate complex multiplication on $\operatorname{BMO}$, cf. [a5].
Calderón–Zygmund operators on ${\bf R} ^ { n }$ form an important class of singular integral operators. A Calderón–Zygmund operator can be defined as a linear operator $T : \mathcal{D} ( \mathbf{R} ^ { n } ) \rightarrow \mathcal{D} ^ { \prime } ( \mathbf{R} ^ { n } )$ with associated Schwarz kernel $K ( x , y )$ defined on $\Omega = \{ ( x , y ) : x , y \in \mathbf{R} ^ { n } , x \neq y \}$ with the following properties:
i) $K$ is locally integrable on $\Omega$ and satisfies $| K ( x , y ) | = O ( | x - y | ^ { - x } )$;
ii) there exist constants $C > 0$ and $0 < \gamma \leq 1$ such that for $( x , y ) \in \Omega$ and $| x ^ { \prime } - x | \leq | x - y | / 2$,
\begin{equation*} | K ( x - , y ) - K ( x , y ) | \leq C | x ^ { \prime } - x | ^ { \gamma } | x - y | ^ { - n - \gamma }. \end{equation*}
Similarly, for $( x , y ) \in \Omega$ and $| y ^ { \prime } - y | \leq | x - y | / 2$,
\begin{equation*} | K ( x , y ^ { \prime } ) - K ( x , y ) | \leq C | y ^ { \prime } - y | ^ { \gamma } | x - y | ^ { - n - \gamma }. \end{equation*}
iii) $T$ can be extended to a bounded linear operator on $L _ { 2 } ( \mathbf{R} ^ { n } )$.
This last condition is hard to verify in general. Thus, it is an important result, known as the $T ( 1 )$-theorem, that if i) and ii) hold, then iii) is equivalent to: $T$ is weakly bounded on $L_{2}$ and both $T ( 1 )$ and $T ^ { * } ( 1 )$ are in $\operatorname{BMO}$, cf. [a3], [a11], [a12]. It is known that diagonal operators with respect to an orthonormal wavelet basis are of Calderón–Zygmund type. This connection with wavelet analysis is treated in [a11].
Many of the results concerning $\operatorname{BMO}$-functions have been generalized to the setting of martingales, cf. [a9] (see also Martingale).
The duality result indicates that $\operatorname{BMO}$ plays a role in complex analysis as well. The class of holomorphic functions (cf. Analytic function) on a domain $D$ with boundary values in $\operatorname{BMO}$ is denoted by 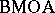 , and is called the
, and is called the 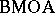 -space, i.e., $= \operatorname{BMOA}= \operatorname{BMO} \cap H ^ { 2 }$.
-space, i.e., $= \operatorname{BMOA}= \operatorname{BMO} \cap H ^ { 2 }$.
Carleson's corona theorem [a5] for the disc states that for given bounded holomorphic functions $f _ { 1 } , \ldots , f _ { n }$ such that $\sum _ { i } | f _ { i } | > \delta > 0$ there exist bounded holomorphic functions $g_ 1 , \ldots , g_ { n }$ such that $\sum _ { i } f _ { i } g _ { i } = 1$. So far (1996), this result could not be extended to the unit ball in $\mathbf{C}^{m}$, $m > 1$, but it can be proved if one only requires that $g_i \in \operatorname { BMOA}$, cf. [a13].
The definition of $\operatorname{BMO}$ makes sense as soon as there are proper notions of integral and ball in a space. Thus, $\operatorname{BMO}$ can be defined in spaces of homogeneous type, cf. [a1], [a2], [a10]. In the setting of several complex variables, several types of $\operatorname{BMO}$-spaces arise on the boundary of (strictly) pseudoconvex domains, depending on whether one considers the isotropic Euclidean balls or the non-isotropic balls that are natural in connection with pseudo-convexity, cf. [a10].
References
| [a1] | R.R. Coifman, G. Weiss, "Analyse harmonique non-commutative sur certains espaces homogènes" , Lecture Notes in Mathematics , 242 , Springer (1971) |
| [a2] | R.R. Coifman, G. Weiss, "Extensions of Hardy spaces and their use in analysis" Bull. Amer. Math. Soc. , 83 (1977) pp. 569–643 |
| [a3] | G. David, J.-L. Journé, "A boundedness criterion for generalized Calderón–Zygmund operators" Ann. of Math. , 120 (1985) pp. 371–397 |
| [a4] | J. Garcia-Cuervas, J.L. Rubio de Francia, "Weighted norm inequalities and related topics" , Math. Stud. , 116 , North-Holland (1985) |
| [a5] | J. Garnett, "Bounded analytic functions" , Acad. Press (1981) |
| [a6] | C. Fefferman, "Characterizations of bounded mean oscillation" Bull. Amer. Math. Soc. , 77 (1971) pp. 587–588 |
| [a7] | C. Fefferman, E.M. Stein, "$H ^ { p }$ spaces of several variables" Acta Math. , 129 (1974) pp. 137–193 |
| [a8] | F. John, L. Nirenberg, "On functions of bounded mean oscillation" Comm. Pure Appl. Math. , 14 (1961) pp. 415–426 |
| [a9] | N. Kazamaki, "Continuous exponential martingales and BMO" , Lecture Notes in Mathematics , 579 , Springer (1994) |
| [a10] | S.G. Krantz, "Geometric analysis and function spaces" , CBMS , 81 , Amer. Math. Soc. (1993) |
| [a11] | Y. Meyer, "Ondelettes et opérateurs II. Opérateurs de Calderón–Zygmund" , Actual. Math. , Hermann (1990) |
| [a12] | E.M. Stein, "Harmonic analysis: real variable methods, orthogonality, and oscillatory integrals" , Math. Ser. , 43 , Princeton Univ. Press (1993) |
| [a13] | N.Th. Varopoulos, "BMO functions and the $\partial$ equation" Pacific J. Math. , 71 (1977) pp. 221–272 |
BMO-space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=BMO-space&oldid=19103