Difference between revisions of "Riemannian geometry in the large"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48559 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | + | The branch of Riemannian geometry that examines the connections between the local and global characteristics of Riemannian manifolds. The term "Riemannian geometry in the large" usually refers to a specific range of problems and methods characteristic for [[Geometry in the large|geometry in the large]]. Fundamental to Riemannian geometry in the large is the study of the connection between the curvature and the topology of a Riemannian manifold. Thus, problems relating to the topological and the metric structure of Riemannian manifolds with given conditions on the curvature are studied, e.g. the question of the existence of a Riemannian metric with prescribed properties of the curvature on a given smooth manifold (the [[Sectional curvature|sectional curvature]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r0821601.png" />; the [[Ricci curvature|Ricci curvature]] Ric; the [[Scalar curvature|scalar curvature]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r0821602.png" />). The major part of the results obtained relate to spaces with curvatures of constant sign. Riemannian geometry in the large is closely connected with the theory of homogeneous spaces (cf. [[Homogeneous space|Homogeneous space]]) and the variational theory of geodesics (cf. [[Geodesic line|Geodesic line]]). For submanifolds of Riemannian manifolds, see [[Isometric immersion|Isometric immersion]] and [[Geometry of immersed manifolds|Geometry of immersed manifolds]]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The branch of Riemannian geometry that examines the connections between the local and global characteristics of Riemannian manifolds. The term "Riemannian geometry in the large" usually refers to a specific range of problems and methods characteristic for [[Geometry in the large|geometry in the large]]. Fundamental to Riemannian geometry in the large is the study of the connection between the curvature and the topology of a Riemannian manifold. Thus, problems relating to the topological and the metric structure of Riemannian manifolds with given conditions on the curvature are studied, e.g. the question of the existence of a Riemannian metric with prescribed properties of the curvature on a given smooth manifold (the [[Sectional curvature|sectional curvature]] | ||
| − | the [[Ricci curvature|Ricci curvature]] Ric; the [[Scalar curvature|scalar curvature]] | ||
| − | The major part of the results obtained relate to spaces with curvatures of constant sign. Riemannian geometry in the large is closely connected with the theory of homogeneous spaces (cf. [[Homogeneous space|Homogeneous space]]) and the variational theory of geodesics (cf. [[Geodesic line|Geodesic line]]). For submanifolds of Riemannian manifolds, see [[Isometric immersion|Isometric immersion]] and [[Geometry of immersed manifolds|Geometry of immersed manifolds]]. | ||
The methods of Riemannian geometry in the large are of a synthetic character. In addition to local differential geometry, wide use is made of the theory of differential equations and [[Morse theory|Morse theory]]. The main achievements are those of the discovery of successful constructions, such as the construction of closed geodesics, of minimal films or of films of geodesics, of horospheres, and of convex sets. The study of the topology of Riemannian manifolds is usually preceded by the study of their metric properties. The latter is often accomplished by comparing a Riemannian manifold with a suitable standard space (see below: Comparison theorems). | The methods of Riemannian geometry in the large are of a synthetic character. In addition to local differential geometry, wide use is made of the theory of differential equations and [[Morse theory|Morse theory]]. The main achievements are those of the discovery of successful constructions, such as the construction of closed geodesics, of minimal films or of films of geodesics, of horospheres, and of convex sets. The study of the topology of Riemannian manifolds is usually preceded by the study of their metric properties. The latter is often accomplished by comparing a Riemannian manifold with a suitable standard space (see below: Comparison theorems). | ||
==Topological structure.== | ==Topological structure.== | ||
| − | For closed surfaces the connection between the curvature and the topology is essentially determined by the Gauss–Bonnet formula (cf. [[Gauss–Bonnet theorem|Gauss–Bonnet theorem]]). Among the closed surfaces, only the sphere | + | For closed surfaces the connection between the curvature and the topology is essentially determined by the Gauss–Bonnet formula (cf. [[Gauss–Bonnet theorem|Gauss–Bonnet theorem]]). Among the closed surfaces, only the sphere <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r0821603.png" /> and the projective plane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r0821604.png" /> can carry a metric of positive curvature; only the torus and the Klein bottle can carry a metric of curvature zero. The structure of a Riemannian manifold of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r0821605.png" /> is less well known (1991). Examples of known theorems are given below. |
| − | and the projective plane | ||
| − | can carry a metric of positive curvature; only the torus and the Klein bottle can carry a metric of curvature zero. The structure of a Riemannian manifold of dimension | ||
| − | is less well known (1991). Examples of known theorems are given below. | ||
| − | A complete simply-connected Riemannian manifold | + | A complete simply-connected Riemannian manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r0821606.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r0821607.png" /> is diffeomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r0821608.png" /> (the Hadamard–Cartan theorem); moreover, for any point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r0821609.png" /> the [[Exponential mapping|exponential mapping]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216010.png" /> is a diffeomorphism of the tangent space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216011.png" /> onto <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216012.png" />. |
| − | with | ||
| − | is diffeomorphic to | ||
| − | the Hadamard–Cartan theorem); moreover, for any point | ||
| − | the [[Exponential mapping|exponential mapping]] | ||
| − | is a diffeomorphism of the tangent space | ||
| − | onto | ||
| − | For closed Riemannian manifolds with | + | For closed Riemannian manifolds with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216013.png" />, the sphere theorem is valid: A complete Riemannian manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216014.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216015.png" /> is called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216018.png" />-pinched; if it is simply connected and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216019.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216020.png" /> is homeomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216021.png" />. For even <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216022.png" /> this bound is precise. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216023.png" /> there are manifolds <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216024.png" /> that are not homeomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216025.png" />: these are the symmetric spaces of rank 1 and only these (cf. [[Symmetric space|Symmetric space]]). For odd <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216026.png" /> the theorem about the homeomorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216027.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216028.png" /> is true even if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216029.png" />. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216030.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216031.png" />, homeomorphism to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216032.png" /> implies diffeomorphism. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216033.png" />, diffeomorphism to the sphere is established with a stronger pinching than in the sphere theorem (it is sufficient to take <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216034.png" />, while if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216035.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216036.png" />). It is also known that with an even stronger pinching (it is sufficient to take <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216037.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216038.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216039.png" />) a non-simply connected <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216040.png" /> is diffeomorphic to a space of constant curvature (the quotient space of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216041.png" /> by a discrete subgroup of isometries). There are a number of results concerning the conditions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216042.png" /> that guarantee homeomorphism to a symmetric space of rank 1 (see [[#References|[14]]], [[#References|[15]]]). |
| − | the sphere theorem is valid: A complete Riemannian manifold | ||
| − | with | ||
| − | is called | ||
| − | pinched; if it is simply connected and | ||
| − | then | ||
| − | is homeomorphic to | ||
| − | For even | ||
| − | this bound is precise. When | ||
| − | there are manifolds | ||
| − | that are not homeomorphic to | ||
| − | these are the symmetric spaces of rank 1 and only these (cf. [[Symmetric space|Symmetric space]]). For odd | ||
| − | the theorem about the homeomorphism of | ||
| − | to | ||
| − | is true even if | ||
| − | When | ||
| − | |||
| − | homeomorphism to | ||
| − | implies diffeomorphism. When | ||
| − | diffeomorphism to the sphere is established with a stronger pinching than in the sphere theorem (it is sufficient to take | ||
| − | while if | ||
| − | |||
| − | It is also known that with an even stronger pinching (it is sufficient to take | ||
| − | |||
| − | |||
| − | a non-simply connected | ||
| − | is diffeomorphic to a space of constant curvature (the quotient space of | ||
| − | by a discrete subgroup of isometries). There are a number of results concerning the conditions on | ||
| − | that guarantee homeomorphism to a symmetric space of rank 1 (see [[#References|[14]]], [[#References|[15]]]). | ||
| − | An open, that is to say, complete non-compact, Riemannian manifold with | + | An open, that is to say, complete non-compact, Riemannian manifold with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216043.png" /> is always diffeomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216044.png" />. A set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216045.png" /> is called absolutely convex if each geodesic with ends in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216046.png" /> lies entirely in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216047.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216048.png" /> be an open Riemannian manifold with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216049.png" />. Then in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216050.png" /> there is a totally geodesic absolutely convex closed submanifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216051.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216052.png" /> is diffeomorphic to the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216053.png" /> of the [[Normal bundle|normal bundle]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216054.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216055.png" /> (if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216056.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216057.png" />). When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216058.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216059.png" />, and always for homogeneous spaces, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216060.png" /> is even isometric to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216061.png" /> with the standard metric of the normal bundle. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216062.png" />, this gives a complete classification of open Riemannian manifolds with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216063.png" />. |
| − | is always diffeomorphic to | ||
| − | A set | ||
| − | is called absolutely convex if each geodesic with ends in | ||
| − | lies entirely in | ||
| − | Let | ||
| − | be an open Riemannian manifold with | ||
| − | Then in | ||
| − | there is a totally geodesic absolutely convex closed submanifold | ||
| − | such that | ||
| − | is diffeomorphic to the space | ||
| − | of the [[Normal bundle|normal bundle]] of | ||
| − | in | ||
| − | if | ||
| − | then | ||
| − | When | ||
| − | or | ||
| − | and always for homogeneous spaces, | ||
| − | is even isometric to | ||
| − | with the standard metric of the normal bundle. When | ||
| − | this gives a complete classification of open Riemannian manifolds with | ||
| − | A straight line is a complete geodesic that is a shortest curve on any segment of it. The cylinder theorem states: An open | + | A straight line is a complete geodesic that is a shortest curve on any segment of it. The cylinder theorem states: An open <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216064.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216065.png" /> is isometric to the direct metric product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216066.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216067.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216068.png" /> does not contain straight lines. The condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216069.png" /> can here be replaced by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216070.png" />. |
| − | with | ||
| − | is isometric to the direct metric product | ||
| − | |||
| − | where | ||
| − | does not contain straight lines. The condition | ||
| − | can here be replaced by | ||
==Fundamental group.== | ==Fundamental group.== | ||
| − | When | + | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216071.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216072.png" /> is even, a closed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216073.png" /> is either orientable and simply connected or non-orientable and the fundamental group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216074.png" />; when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216075.png" /> is odd, it is always orientable but little is known about <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216076.png" /> beyond the limits of the sphere theorem. Even for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216077.png" /> of constant curvature <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216078.png" />, the full description of the possible structures of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216079.png" /> for odd <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216080.png" /> turned out to be a difficult problem (see [[#References|[9]]]). |
| − | |||
| − | is even, a closed | ||
| − | is either orientable and simply connected or non-orientable and the fundamental group | ||
| − | when | ||
| − | is odd, it is always orientable but little is known about | ||
| − | beyond the limits of the sphere theorem. Even for | ||
| − | of constant curvature | ||
| − | the full description of the possible structures of | ||
| − | for odd | ||
| − | turned out to be a difficult problem (see [[#References|[9]]]). | ||
| − | If | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216081.png" />, then the universal covering <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216082.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216083.png" /> is isometric to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216084.png" /> and the fundamental group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216085.png" /> is isomorphic to a discrete group of isometries of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216086.png" /> without fixed points; it contains the subgroup of translations as a subgroup of finite index. (Thus, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216087.png" /> permits a finite isometric covering by a flat torus.) |
| − | then the universal covering | ||
| − | of | ||
| − | is isometric to | ||
| − | and the fundamental group | ||
| − | is isomorphic to a discrete group of isometries of | ||
| − | without fixed points; it contains the subgroup of translations as a subgroup of finite index. (Thus, | ||
| − | permits a finite isometric covering by a flat torus.) | ||
| − | If | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216088.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216089.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216090.png" /> is diffeomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216091.png" />. Therefore all homotopy groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216092.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216093.png" /> are trivial and the homotopy type is determined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216094.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216095.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216096.png" /> is completely non-commutative in the sense that any of its Abelian (and even any of its solvable) subgroups is an infinite cyclic group. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216097.png" />, the following is known. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216098.png" /> be a solvable subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r08216099.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160100.png" /> is isomorphic to a discrete group of isometries of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160101.png" /> (without fixed points) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160102.png" /> contains a compact totally geodesic submanifold which is isometric to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160103.png" />. Instead of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160104.png" /> it is sufficient in this case to require the absence of conjugate points on the geodesics. |
| − | on | ||
| − | then | ||
| − | is diffeomorphic to | ||
| − | Therefore all homotopy groups | ||
| − | for | ||
| − | are trivial and the homotopy type is determined by | ||
| − | If | ||
| − | then | ||
| − | is completely non-commutative in the sense that any of its Abelian (and even any of its solvable) subgroups is an infinite cyclic group. When | ||
| − | the following is known. Let | ||
| − | be a solvable subgroup of | ||
| − | Then | ||
| − | is isomorphic to a discrete group of isometries of | ||
| − | without fixed points) and | ||
| − | contains a compact totally geodesic submanifold which is isometric to | ||
| − | Instead of | ||
| − | it is sufficient in this case to require the absence of conjugate points on the geodesics. | ||
| − | For two manifolds of the same constant negative curvature and the same dimension | + | For two manifolds of the same constant negative curvature and the same dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160105.png" />, isomorphism of their <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160106.png" />'s implies isometry (Mostow's rigidity theorem). |
| − | isomorphism of their | ||
| − | s implies isometry (Mostow's rigidity theorem). | ||
| − | Riemannian manifolds for which | + | Riemannian manifolds for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160107.png" /> are called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160109.png" />-flat. For an arbitrary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160110.png" /> such manifolds can be topologically different from locally flat manifolds. For them, for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160111.png" />, there is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160112.png" /> such that for an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160113.png" />-flat <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160114.png" /> there is a nilpotent subgroup of finite index in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160115.png" />. In this case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160116.png" /> permits a finite (with multiplicity dependent only on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160117.png" />) covering diffeomorphic to the quotient space of a nilpotent Lie group by a discrete subgroup of it (see [[#References|[8]]]). |
| − | are called | ||
| − | flat. For an arbitrary | ||
| − | such manifolds can be topologically different from locally flat manifolds. For them, for any | ||
| − | there is an | ||
| − | such that for an | ||
| − | flat | ||
| − | there is a nilpotent subgroup of finite index in | ||
| − | In this case | ||
| − | permits a finite (with multiplicity dependent only on | ||
| − | covering diffeomorphic to the quotient space of a nilpotent Lie group by a discrete subgroup of it (see [[#References|[8]]]). | ||
| − | A complete Riemannian manifold with curvature | + | A complete Riemannian manifold with curvature <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160118.png" /> has finite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160119.png" /> and thus a finite group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160120.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160121.png" /> for a closed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160122.png" />, there is a finite normal subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160123.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160124.png" /> is a discrete group of isometries of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160125.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160126.png" />; moreover, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160127.png" /> decomposes into the direct metric product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160128.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160129.png" /> is closed, the decomposition is invariant relative to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160130.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160131.png" /> is trivial in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160132.png" />. |
| − | has finite | ||
| − | and thus a finite group | ||
| − | If | ||
| − | for a closed | ||
| − | there is a finite normal subgroup | ||
| − | such that | ||
| − | is a discrete group of isometries of | ||
| − | |||
| − | moreover, | ||
| − | decomposes into the direct metric product | ||
| − | where | ||
| − | is closed, the decomposition is invariant relative to | ||
| − | and | ||
| − | is trivial in | ||
| − | In addition to the study of | + | In addition to the study of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160133.png" />, several estimates of the Betti numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160134.png" /> have been made using the theory of harmonic differential forms for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160135.png" />-pinched <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160136.png" />. Thus, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160137.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160138.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160139.png" /> is odd. |
| − | several estimates of the Betti numbers | ||
| − | have been made using the theory of harmonic differential forms for | ||
| − | pinched | ||
| − | Thus, | ||
| − | when | ||
| − | and | ||
| − | is odd. | ||
==Comparison theorems.== | ==Comparison theorems.== | ||
| − | Many global properties of Riemannian manifolds are proved by comparing the structures in the Riemannian manifolds under consideration to similar structures on a standard space. This usually is a manifold of constant curvature, or, more rarely, another symmetric space. Below, a | + | Many global properties of Riemannian manifolds are proved by comparing the structures in the Riemannian manifolds under consideration to similar structures on a standard space. This usually is a manifold of constant curvature, or, more rarely, another symmetric space. Below, a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160141.png" />-plane is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160142.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160143.png" />, the sphere <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160144.png" /> of radius <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160145.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160146.png" /> and the Lobachevskii plane of curvature <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160147.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160148.png" />. |
| − | plane is | ||
| − | when | ||
| − | the sphere | ||
| − | of radius | ||
| − | when | ||
| − | and the Lobachevskii plane of curvature | ||
| − | when | ||
| − | The Toponogov theorem on the comparison of angles has many applications: In a Riemannian manifold | + | The Toponogov theorem on the comparison of angles has many applications: In a Riemannian manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160149.png" />, let all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160150.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160151.png" /> be the angles of a triangle made of shortest curves, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160152.png" /> be the corresponding angles of a triangle with sides of the same length in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160153.png" />-plane; then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160154.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160155.png" /> and if any two points of the sides of the triangle in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160156.png" /> in question can be joined by a single shortest curve, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160157.png" />. This theorem is equivalent to the following convexity condition: If in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160158.png" /> the shortest curves <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160159.png" /> form the same angle as the shortest curves <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160160.png" /> of the same length in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160161.png" />-plane, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160162.png" />. What is being compared here is essentially the rate of divergence of the shortest curves. |
| − | let all | ||
| − | let | ||
| − | be the angles of a triangle made of shortest curves, and let | ||
| − | be the corresponding angles of a triangle with sides of the same length in the | ||
| − | plane; then | ||
| − | If | ||
| − | and if any two points of the sides of the triangle in | ||
| − | in question can be joined by a single shortest curve, then | ||
| − | This theorem is equivalent to the following convexity condition: If in | ||
| − | the shortest curves | ||
| − | form the same angle as the shortest curves | ||
| − | of the same length in the | ||
| − | plane, then | ||
| − | What is being compared here is essentially the rate of divergence of the shortest curves. | ||
| − | Rauch's comparison theorem compares the rate of movement of the end points | + | Rauch's comparison theorem compares the rate of movement of the end points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160163.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160164.png" /> of two shortest curves <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160165.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160166.png" /> in two Riemannian manifolds <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160167.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160168.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160169.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160170.png" /> turn around their origins <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160171.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160172.png" /> with the same rate, under conditions when (in a natural comparison) the sectional curvatures in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160173.png" /> are not less than in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160174.png" />. Then the rate of movement of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160175.png" /> is not greater than the rate of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160176.png" />. In the fundamental case (comparison with a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160177.png" />-plane), Rauch's theorem is equivalent to the infinitesimal version of the theorem on the comparison of angles. |
| − | and | ||
| − | of two shortest curves | ||
| − | |||
| − | in two Riemannian manifolds | ||
| − | and | ||
| − | when | ||
| − | and | ||
| − | turn around their origins | ||
| − | |||
| − | with the same rate, under conditions when (in a natural comparison) the sectional curvatures in | ||
| − | are not less than in | ||
| − | Then the rate of movement of | ||
| − | is not greater than the rate of | ||
| − | In the fundamental case (comparison with a | ||
| − | plane), Rauch's theorem is equivalent to the infinitesimal version of the theorem on the comparison of angles. | ||
| − | There are theorems similar to Rauch's in which the points | + | There are theorems similar to Rauch's in which the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160178.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160179.png" /> move on hypersurfaces to which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160180.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160181.png" /> remain orthogonal. There are also comparison theorems for volumes of tubular neighbourhoods of submanifolds (see [[#References|[13]]], [[#References|[16]]]). |
| − | |||
| − | move on hypersurfaces to which | ||
| − | |||
| − | remain orthogonal. There are also comparison theorems for volumes of tubular neighbourhoods of submanifolds (see [[#References|[13]]], [[#References|[16]]]). | ||
==Extremal theorems.== | ==Extremal theorems.== | ||
| − | Comparison theorems lead to estimates of such characteristics of | + | Comparison theorems lead to estimates of such characteristics of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160182.png" /> as the diameter, the radius of injectivity, the length of a closed geodesic, the volume of a sphere of given radius, etc. Extremal theorems give answers to questions concerning cases of achieving equality in such estimates. |
| − | as the diameter, the radius of injectivity, the length of a closed geodesic, the volume of a sphere of given radius, etc. Extremal theorems give answers to questions concerning cases of achieving equality in such estimates. | ||
| − | For | + | For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160183.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160184.png" /> one always has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160185.png" />. Equality is achieved only for the unit sphere. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160186.png" /> is closed and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160187.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160188.png" /> is even or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160189.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160190.png" /> is odd, then the radius of injectivity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160191.png" /> and the length of a closed geodesic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160192.png" />. If in this case there is a closed geodesic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160193.png" /> of length <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160194.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160195.png" />, then, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160196.png" /> is even, there is a totally geodesic surface in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160197.png" /> which contains <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160198.png" /> and which is isometric to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160199.png" />, while if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160200.png" />, independently of the parity of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160201.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160202.png" /> is isometric to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160203.png" /> (see [[#References|[6]]]). The volume of a sphere <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160204.png" /> of radius <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160205.png" /> in an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160206.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160207.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160208.png" /> is not less (not greater) than the volume of the sphere <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160209.png" /> of the same radius in the space of constant curvature <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160210.png" />, with equality only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160211.png" /> is isometric to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160212.png" />. |
| − | with | ||
| − | one always has | ||
| − | Equality is achieved only for the unit sphere. If | ||
| − | is closed and | ||
| − | |||
| − | is even or | ||
| − | |||
| − | is odd, then the radius of injectivity | ||
| − | and the length of a closed geodesic | ||
| − | If in this case there is a closed geodesic | ||
| − | of length | ||
| − | in | ||
| − | then, if | ||
| − | is even, there is a totally geodesic surface in | ||
| − | which contains | ||
| − | and which is isometric to | ||
| − | while if | ||
| − | independently of the parity of | ||
| − | |||
| − | is isometric to | ||
| − | see [[#References|[6]]]). The volume of a sphere | ||
| − | of radius | ||
| − | in an | ||
| − | with | ||
| − | |||
| − | is not less (not greater) than the volume of the sphere | ||
| − | of the same radius in the space of constant curvature | ||
| − | with equality only if | ||
| − | is isometric to | ||
| − | Extremal theorems are not always connected with estimates of the curvature. For example, for any point in a closed surface | + | Extremal theorems are not always connected with estimates of the curvature. For example, for any point in a closed surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160213.png" />, let the set of points conjugate to it consist of a single point. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160214.png" /> is isometric to a sphere. |
| − | let the set of points conjugate to it consist of a single point. Then | ||
| − | is isometric to a sphere. | ||
==Finiteness of topological types.== | ==Finiteness of topological types.== | ||
| − | Among the closed Riemannian manifolds with uniformly bounded curvatures and radii of injectivity bounded from below, | + | Among the closed Riemannian manifolds with uniformly bounded curvatures and radii of injectivity bounded from below, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160215.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160216.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160217.png" />, only finitely many are homotopically pairwise non-equivalent, and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160218.png" /> is changed into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160219.png" />, only finitely many of them are pairwise non-homeomorphic. In this statement the condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160220.png" /> can be replaced by the conditions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160221.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160222.png" />, which imply it but are more easily verifiable (see [[#References|[14]]]). |
| − | |||
| − | |||
| − | only finitely many are homotopically pairwise non-equivalent, and if | ||
| − | is changed into | ||
| − | only finitely many of them are pairwise non-homeomorphic. In this statement the condition | ||
| − | can be replaced by the conditions | ||
| − | |||
| − | which imply it but are more easily verifiable (see [[#References|[14]]]). | ||
| − | For a Riemannian manifold with | + | For a Riemannian manifold with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160223.png" /> of fixed sign, the conditions that guarantee the finiteness of its topological type are simplified. For example, for even <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160224.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160225.png" /> the condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160226.png" /> is sufficient. |
| − | of fixed sign, the conditions that guarantee the finiteness of its topological type are simplified. For example, for even | ||
| − | and | ||
| − | the condition | ||
| − | is sufficient. | ||
| − | When | + | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160227.png" />, for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160228.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160229.png" /> the estimate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160230.png" /> is true. Therefore, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160231.png" />, the number of topological types of closed Riemannian manifolds that satisfy the conditions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160232.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160233.png" />, is finite. But when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160234.png" />, there is an infinite number of pairwise non-homeomorphic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160235.png" /> satisfying these conditions (see [[#References|[12]]]). |
| − | for | ||
| − | with | ||
| − | the estimate | ||
| − | is true. Therefore, when | ||
| − | the number of topological types of closed Riemannian manifolds that satisfy the conditions | ||
| − | |||
| − | is finite. But when | ||
| − | there is an infinite number of pairwise non-homeomorphic | ||
| − | satisfying these conditions (see [[#References|[12]]]). | ||
==Metrics with prescribed curvature.== | ==Metrics with prescribed curvature.== | ||
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160236.png" /> be the [[Euler characteristic|Euler characteristic]] of a closed surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160237.png" />. In order that a smooth function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160238.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160239.png" /> be the curvature of a Riemannian metric in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160240.png" /> it is necessary that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160241.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160242.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160243.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160244.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160245.png" /> changes sign or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160246.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160247.png" />. These conditions are also sufficient. The condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160248.png" /> is necessary and sufficient for the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160249.png" />-form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160250.png" /> to be the [[Curvature form|curvature form]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160251.png" /> of a Riemannian metric in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160252.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160253.png" /> is an open submanifold of a closed manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160254.png" />, then any smooth <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160255.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160256.png" /> is the curvature of a (possibly incomplete) Riemannian metric in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160257.png" />. Necessary and sufficient conditions under which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160258.png" /> is the curvature of a complete Riemannian metric in a non-compact surface have been ascertained for finitely-connected surfaces. |
| − | be the [[Euler characteristic|Euler characteristic]] of a closed surface | ||
| − | In order that a smooth function | ||
| − | on | ||
| − | be the curvature of a Riemannian metric in | ||
| − | it is necessary that | ||
| − | |||
| − | |||
| − | when | ||
| − | and | ||
| − | changes sign or | ||
| − | when | ||
| − | These conditions are also sufficient. The condition | ||
| − | is necessary and sufficient for the | ||
| − | form | ||
| − | to be the [[Curvature form|curvature form]] | ||
| − | of a Riemannian metric in | ||
| − | If | ||
| − | is an open submanifold of a closed manifold | ||
| − | then any smooth | ||
| − | on | ||
| − | is the curvature of a (possibly incomplete) Riemannian metric in | ||
| − | Necessary and sufficient conditions under which | ||
| − | is the curvature of a complete Riemannian metric in a non-compact surface have been ascertained for finitely-connected surfaces. | ||
| − | As the dimension increases, the number of independent components of the curvature tensor increases faster than the number of components of the metric tensor. The conditions under which the given tensor field is, at least locally, the field of the curvature tensor of a certain metric are unknown (1991). But for the scalar curvature, when | + | As the dimension increases, the number of independent components of the curvature tensor increases faster than the number of components of the metric tensor. The conditions under which the given tensor field is, at least locally, the field of the curvature tensor of a certain metric are unknown (1991). But for the scalar curvature, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160259.png" />, each smooth function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160260.png" /> on a closed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160261.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160262.png" /> is the scalar curvature of a Riemannian metric in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160263.png" /> (see [[#References|[4]]]). There are manifolds which do not permit a metric with a positive scalar curvature, as is the case with a three-dimensional torus (see [[#References|[5]]]). |
| − | each smooth function | ||
| − | on a closed | ||
| − | for which | ||
| − | is the scalar curvature of a Riemannian metric in | ||
| − | see [[#References|[4]]]). There are manifolds which do not permit a metric with a positive scalar curvature, as is the case with a three-dimensional torus (see [[#References|[5]]]). | ||
==Convex functions.== | ==Convex functions.== | ||
| − | The existence of a scalar function | + | The existence of a scalar function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160264.png" /> on a Riemannian manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160265.png" /> that is convex along any geodesic imposes strict limitations on the structure of such an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160266.png" />. For example, if there is a convex function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160267.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160268.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160269.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160270.png" /> is strictly convex and if for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160271.png" /> the sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160272.png" /> are compact, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160273.png" /> is diffeomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160274.png" />. |
| − | on a Riemannian manifold | ||
| − | that is convex along any geodesic imposes strict limitations on the structure of such an | ||
| − | For example, if there is a convex function | ||
| − | on | ||
| − | then | ||
| − | If | ||
| − | is strictly convex and if for any | ||
| − | the sets | ||
| − | are compact, then | ||
| − | is diffeomorphic to | ||
| − | Convex functions can be constructed in a number of cases. For example, when | + | Convex functions can be constructed in a number of cases. For example, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160275.png" />, the functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160276.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160277.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160278.png" />, are convex. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160279.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160280.png" /> is an isometry, then the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160281.png" /> is convex. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160282.png" />, there are convex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160283.png" /> with compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160284.png" />; this is connected with the absolute convexity (when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160285.png" />) of the complements to horospheres and with the fact that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160286.png" />, then the convexity of a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160287.png" /> implies the convexity of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160288.png" />. |
| − | the functions | ||
| − | |||
| − | |||
| − | are convex. If | ||
| − | and | ||
| − | is an isometry, then the function | ||
| − | is convex. When | ||
| − | there are convex | ||
| − | with compact | ||
| − | this is connected with the absolute convexity (when | ||
| − | of the complements to horospheres and with the fact that if | ||
| − | then the convexity of a set | ||
| − | implies the convexity of the set | ||
Problems of Riemannian geometry in the large have also been studied for Riemannian manifolds with additional structures, such as for Kähler manifolds (see [[#References|[10]]]). | Problems of Riemannian geometry in the large have also been studied for Riemannian manifolds with additional structures, such as for Kähler manifolds (see [[#References|[10]]]). | ||
| Line 354: | Line 66: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> Yu.D. Burago, V.A. Zalgaller, "Convex sets in Riemannian spaces of non-negative curvature" ''Russian Math. Surveys'' , '''32''' : 3 (1977) pp. 1–57 ''Uspekhi Mat. Nauk'' , '''32''' : 3 (1977) pp. 3–55</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Cheeger, D.G. Ebin, "Comparison theorems in Riemannian geometry" , North-Holland (1975)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> , ''Research on the metric theory of surfaces'' , Moscow (1980) (In Russian; translated from English and French)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> R. Schoen, S.-T. Yau, "Existence of incompressible minimal surfaces and the topology of three-dimensional manifolds with non-negative scalar curvature" ''Ann. of Math.'' , '''110''' (1979) pp. 127–142</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> V.A. Toponogov, "Extremal theorems for Riemann spaces with curvature bounded above I" ''Sib. Math. J.'' , '''15''' : 6 (1974) pp. 954–971 ''Sibirsk. Mat. Zh.'' , '''15''' : 6 (1974) pp. 1348–1371</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> M. Gromov, H.B., jr. Lawson, "Spin and scalar curvature in the presence of a fundamental group I" ''Ann. of Math.'' , '''111''' : 2 (1980) pp. 209–230</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> P. Buser, H. Karcher, "Gromov's almost flat manifolds" ''Astérique'' , '''81''' (1981)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> J.A. Wolf, "Spaces of constant curvature" , Publish or Perish (1977)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> S.I. Goldberg, "Curvature and homology" , Acad. Press (1962)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> A.L. Besse, "Manifolds all of whose geodesics are closed" , Springer (1978)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> W. Thurston, "The geometry and topology of 3-manifolds" , Princeton Univ. Press (1978) (Preprint)</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> E. Heintze, H. Karcher, "A general comparison theorem with applications to volume estimates for submanifolds" ''Ann. Sci. Ecole Norm. Sup.'' , '''11''' : 4 (1978) pp. 451–470</TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> J. Cheeger, "Pinching theorems for a certain class of Riemannian manifolds" ''Amer. J. Math.'' , '''91''' : 3 (1969) pp. 807–834</TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> Min-Do, E. Ruh, "Comparison theorems for compact symmetric spaces" ''Ann. Sci. Ecole Norm. Sup.'' , '''12''' (1979) pp. 335–353</TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> A. Gray, "Comparison theorems for the volumes of tubes as generalizations of the Weyl tube formula" ''Topology'' , '''21''' : 2 (1982) pp. 201–228</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> Yu.D. Burago, V.A. Zalgaller, "Convex sets in Riemannian spaces of non-negative curvature" ''Russian Math. Surveys'' , '''32''' : 3 (1977) pp. 1–57 ''Uspekhi Mat. Nauk'' , '''32''' : 3 (1977) pp. 3–55</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Cheeger, D.G. Ebin, "Comparison theorems in Riemannian geometry" , North-Holland (1975)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> , ''Research on the metric theory of surfaces'' , Moscow (1980) (In Russian; translated from English and French)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> R. Schoen, S.-T. Yau, "Existence of incompressible minimal surfaces and the topology of three-dimensional manifolds with non-negative scalar curvature" ''Ann. of Math.'' , '''110''' (1979) pp. 127–142</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> V.A. Toponogov, "Extremal theorems for Riemann spaces with curvature bounded above I" ''Sib. Math. J.'' , '''15''' : 6 (1974) pp. 954–971 ''Sibirsk. Mat. Zh.'' , '''15''' : 6 (1974) pp. 1348–1371</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> M. Gromov, H.B., jr. Lawson, "Spin and scalar curvature in the presence of a fundamental group I" ''Ann. of Math.'' , '''111''' : 2 (1980) pp. 209–230</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> P. Buser, H. Karcher, "Gromov's almost flat manifolds" ''Astérique'' , '''81''' (1981)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> J.A. Wolf, "Spaces of constant curvature" , Publish or Perish (1977)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> S.I. Goldberg, "Curvature and homology" , Acad. Press (1962)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> A.L. Besse, "Manifolds all of whose geodesics are closed" , Springer (1978)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> W. Thurston, "The geometry and topology of 3-manifolds" , Princeton Univ. Press (1978) (Preprint)</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> E. Heintze, H. Karcher, "A general comparison theorem with applications to volume estimates for submanifolds" ''Ann. Sci. Ecole Norm. Sup.'' , '''11''' : 4 (1978) pp. 451–470</TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> J. Cheeger, "Pinching theorems for a certain class of Riemannian manifolds" ''Amer. J. Math.'' , '''91''' : 3 (1969) pp. 807–834</TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> Min-Do, E. Ruh, "Comparison theorems for compact symmetric spaces" ''Ann. Sci. Ecole Norm. Sup.'' , '''12''' (1979) pp. 335–353</TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> A. Gray, "Comparison theorems for the volumes of tubes as generalizations of the Weyl tube formula" ''Topology'' , '''21''' : 2 (1982) pp. 201–228</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
For some more results on the interrelations between curvature and fundamental group cf. (the editorial comments to) [[Polycyclic group|Polycyclic group]] and [[Polynomial and exponential growth in groups and algebras|Polynomial and exponential growth in groups and algebras]]. | For some more results on the interrelations between curvature and fundamental group cf. (the editorial comments to) [[Polycyclic group|Polycyclic group]] and [[Polynomial and exponential growth in groups and algebras|Polynomial and exponential growth in groups and algebras]]. | ||
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160289.png" /> be a unit length tangent vector at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160290.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160291.png" /> be its geodesic. For sufficiently small <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160292.png" /> the distance between the starting point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160293.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160294.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160295.png" />, but this may fail for larger <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160296.png" />. The cut value function (on the sphere subbundle of the tangent bundle) is defined by |
| − | be a unit length tangent vector at | ||
| − | Let | ||
| − | be its geodesic. For sufficiently small | ||
| − | the distance between the starting point | ||
| − | and | ||
| − | is | ||
| − | but this may fail for larger | ||
| − | The cut value function (on the sphere subbundle of the tangent bundle) is defined by | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160297.png" /></td> </tr></table> | |
| − | |||
| − | The cut locus of | + | The cut locus of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160298.png" /> is by definition the set of points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160299.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160300.png" /> runs over all unit length tangent vectors at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160301.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160302.png" /> is the exponential mapping at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160303.png" />; cf. [[Exponential mapping|Exponential mapping]] and the subsection "Exponential mapping" in [[Riemannian geometry|Riemannian geometry]]. |
| − | is by definition the set of points | ||
| − | where | ||
| − | runs over all unit length tangent vectors at | ||
| − | and | ||
| − | is the exponential mapping at | ||
| − | cf. [[Exponential mapping|Exponential mapping]] and the subsection "Exponential mapping" in [[Riemannian geometry|Riemannian geometry]]. | ||
| − | The radius of injectivity, | + | The radius of injectivity, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160304.png" />, at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160305.png" /> is defined as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160306.png" />, and the global radius of injectivity of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160307.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160308.png" />. It is always positive if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160309.png" /> is compact, but can be zero if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160310.png" /> is non-compact. |
| − | at | ||
| − | is defined as | ||
| − | and the global radius of injectivity of | ||
| − | is | ||
| − | It is always positive if | ||
| − | is compact, but can be zero if | ||
| − | is non-compact. | ||
| − | The cut locus was introduced by H. Poincaré under the name "ligne de partage" . Every compact surface admits a Riemannian metric of constant curvature. "Cutting up" a higher-genus surface | + | The cut locus was introduced by H. Poincaré under the name "ligne de partage" . Every compact surface admits a Riemannian metric of constant curvature. "Cutting up" a higher-genus surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160311.png" /> along a cut locus yields a particularly nice representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082160/r082160312.png" /> as a domain bounded by a polygon on which edges are pairwise identified, [[#References|[a3]]]. For the sphere, the genus 0 case, the cut locus of a point is the single diametrically-opposite point. |
| − | along a cut locus yields a particularly nice representation of | ||
| − | as a domain bounded by a polygon on which edges are pairwise identified, [[#References|[a3]]]. For the sphere, the genus 0 case, the cut locus of a point is the single diametrically-opposite point. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) pp. Sect. 11.4 (Translated from French)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) pp. Chapt. 2 (Translated from German)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> S. Gallot, D. Hulin, J. Lafontaine, "Riemannian geometry" , Springer (1987) (Translated from French)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> W.M. Boothby, "An introduction to differentiable manifolds and Riemannian geometry" , Acad. Press (1975)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> W. Greub, S. Halperin, R. Vanstone, "Connections, curvature, and cohomology" , '''1–3''' , Acad. Press (1972–1976)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) pp. Sect. 11.4 (Translated from French)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) pp. Chapt. 2 (Translated from German)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> S. Gallot, D. Hulin, J. Lafontaine, "Riemannian geometry" , Springer (1987) (Translated from French)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> W.M. Boothby, "An introduction to differentiable manifolds and Riemannian geometry" , Acad. Press (1975)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> W. Greub, S. Halperin, R. Vanstone, "Connections, curvature, and cohomology" , '''1–3''' , Acad. Press (1972–1976)</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
The branch of Riemannian geometry that examines the connections between the local and global characteristics of Riemannian manifolds. The term "Riemannian geometry in the large" usually refers to a specific range of problems and methods characteristic for geometry in the large. Fundamental to Riemannian geometry in the large is the study of the connection between the curvature and the topology of a Riemannian manifold. Thus, problems relating to the topological and the metric structure of Riemannian manifolds with given conditions on the curvature are studied, e.g. the question of the existence of a Riemannian metric with prescribed properties of the curvature on a given smooth manifold (the sectional curvature 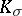 ; the Ricci curvature Ric; the scalar curvature
; the Ricci curvature Ric; the scalar curvature 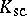 ). The major part of the results obtained relate to spaces with curvatures of constant sign. Riemannian geometry in the large is closely connected with the theory of homogeneous spaces (cf. Homogeneous space) and the variational theory of geodesics (cf. Geodesic line). For submanifolds of Riemannian manifolds, see Isometric immersion and Geometry of immersed manifolds.
). The major part of the results obtained relate to spaces with curvatures of constant sign. Riemannian geometry in the large is closely connected with the theory of homogeneous spaces (cf. Homogeneous space) and the variational theory of geodesics (cf. Geodesic line). For submanifolds of Riemannian manifolds, see Isometric immersion and Geometry of immersed manifolds.
The methods of Riemannian geometry in the large are of a synthetic character. In addition to local differential geometry, wide use is made of the theory of differential equations and Morse theory. The main achievements are those of the discovery of successful constructions, such as the construction of closed geodesics, of minimal films or of films of geodesics, of horospheres, and of convex sets. The study of the topology of Riemannian manifolds is usually preceded by the study of their metric properties. The latter is often accomplished by comparing a Riemannian manifold with a suitable standard space (see below: Comparison theorems).
Topological structure.
For closed surfaces the connection between the curvature and the topology is essentially determined by the Gauss–Bonnet formula (cf. Gauss–Bonnet theorem). Among the closed surfaces, only the sphere 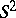 and the projective plane
and the projective plane 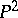 can carry a metric of positive curvature; only the torus and the Klein bottle can carry a metric of curvature zero. The structure of a Riemannian manifold of dimension
can carry a metric of positive curvature; only the torus and the Klein bottle can carry a metric of curvature zero. The structure of a Riemannian manifold of dimension 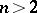 is less well known (1991). Examples of known theorems are given below.
is less well known (1991). Examples of known theorems are given below.
A complete simply-connected Riemannian manifold 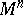 with
with 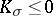 is diffeomorphic to
is diffeomorphic to 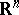 (the Hadamard–Cartan theorem); moreover, for any point
(the Hadamard–Cartan theorem); moreover, for any point 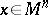 the exponential mapping
the exponential mapping 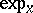 is a diffeomorphism of the tangent space
is a diffeomorphism of the tangent space 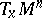 onto
onto 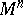 .
.
For closed Riemannian manifolds with 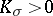 , the sphere theorem is valid: A complete Riemannian manifold
, the sphere theorem is valid: A complete Riemannian manifold 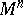 with
with  is called
is called 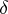 -pinched; if it is simply connected and
-pinched; if it is simply connected and 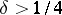 , then
, then 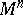 is homeomorphic to
is homeomorphic to  . For even
. For even  this bound is precise. When
this bound is precise. When 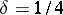 there are manifolds
there are manifolds 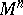 that are not homeomorphic to
that are not homeomorphic to 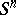 : these are the symmetric spaces of rank 1 and only these (cf. Symmetric space). For odd
: these are the symmetric spaces of rank 1 and only these (cf. Symmetric space). For odd  the theorem about the homeomorphism of
the theorem about the homeomorphism of  to
to 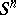 is true even if
is true even if 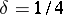 . When
. When 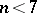 ,
, 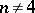 , homeomorphism to
, homeomorphism to 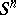 implies diffeomorphism. When
implies diffeomorphism. When 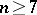 , diffeomorphism to the sphere is established with a stronger pinching than in the sphere theorem (it is sufficient to take
, diffeomorphism to the sphere is established with a stronger pinching than in the sphere theorem (it is sufficient to take  , while if
, while if 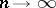 ,
, 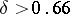 ). It is also known that with an even stronger pinching (it is sufficient to take
). It is also known that with an even stronger pinching (it is sufficient to take 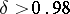 and
and 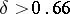 as
as  ) a non-simply connected
) a non-simply connected  is diffeomorphic to a space of constant curvature (the quotient space of
is diffeomorphic to a space of constant curvature (the quotient space of 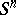 by a discrete subgroup of isometries). There are a number of results concerning the conditions on
by a discrete subgroup of isometries). There are a number of results concerning the conditions on 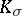 that guarantee homeomorphism to a symmetric space of rank 1 (see [14], [15]).
that guarantee homeomorphism to a symmetric space of rank 1 (see [14], [15]).
An open, that is to say, complete non-compact, Riemannian manifold with 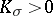 is always diffeomorphic to
is always diffeomorphic to 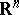 . A set
. A set 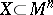 is called absolutely convex if each geodesic with ends in
is called absolutely convex if each geodesic with ends in 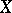 lies entirely in
lies entirely in 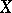 . Let
. Let 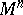 be an open Riemannian manifold with
be an open Riemannian manifold with 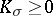 . Then in
. Then in 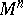 there is a totally geodesic absolutely convex closed submanifold
there is a totally geodesic absolutely convex closed submanifold  such that
such that 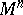 is diffeomorphic to the space
is diffeomorphic to the space 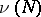 of the normal bundle of
of the normal bundle of 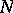 in
in 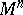 (if
(if 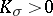 , then
, then 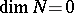 ). When
). When 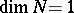 or
or 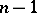 , and always for homogeneous spaces,
, and always for homogeneous spaces, 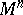 is even isometric to
is even isometric to 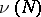 with the standard metric of the normal bundle. When
with the standard metric of the normal bundle. When 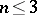 , this gives a complete classification of open Riemannian manifolds with
, this gives a complete classification of open Riemannian manifolds with 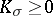 .
.
A straight line is a complete geodesic that is a shortest curve on any segment of it. The cylinder theorem states: An open  with
with 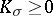 is isometric to the direct metric product
is isometric to the direct metric product 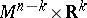 ,
, 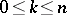 , where
, where 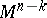 does not contain straight lines. The condition
does not contain straight lines. The condition 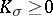 can here be replaced by
can here be replaced by 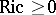 .
.
Fundamental group.
When 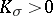 and
and  is even, a closed
is even, a closed 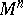 is either orientable and simply connected or non-orientable and the fundamental group
is either orientable and simply connected or non-orientable and the fundamental group 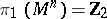 ; when
; when  is odd, it is always orientable but little is known about
is odd, it is always orientable but little is known about 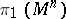 beyond the limits of the sphere theorem. Even for
beyond the limits of the sphere theorem. Even for 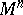 of constant curvature
of constant curvature 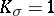 , the full description of the possible structures of
, the full description of the possible structures of 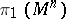 for odd
for odd  turned out to be a difficult problem (see [9]).
turned out to be a difficult problem (see [9]).
If 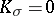 , then the universal covering
, then the universal covering 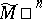 of
of 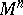 is isometric to
is isometric to  and the fundamental group
and the fundamental group 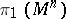 is isomorphic to a discrete group of isometries of
is isomorphic to a discrete group of isometries of 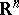 without fixed points; it contains the subgroup of translations as a subgroup of finite index. (Thus,
without fixed points; it contains the subgroup of translations as a subgroup of finite index. (Thus, 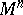 permits a finite isometric covering by a flat torus.)
permits a finite isometric covering by a flat torus.)
If 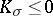 on
on 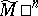 , then
, then 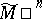 is diffeomorphic to
is diffeomorphic to 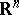 . Therefore all homotopy groups
. Therefore all homotopy groups 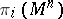 for
for 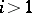 are trivial and the homotopy type is determined by
are trivial and the homotopy type is determined by 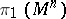 . If
. If 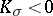 , then
, then 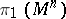 is completely non-commutative in the sense that any of its Abelian (and even any of its solvable) subgroups is an infinite cyclic group. When
is completely non-commutative in the sense that any of its Abelian (and even any of its solvable) subgroups is an infinite cyclic group. When 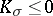 , the following is known. Let
, the following is known. Let 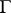 be a solvable subgroup of
be a solvable subgroup of 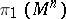 . Then
. Then 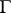 is isomorphic to a discrete group of isometries of
is isomorphic to a discrete group of isometries of 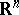 (without fixed points) and
(without fixed points) and 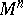 contains a compact totally geodesic submanifold which is isometric to
contains a compact totally geodesic submanifold which is isometric to  . Instead of
. Instead of 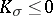 it is sufficient in this case to require the absence of conjugate points on the geodesics.
it is sufficient in this case to require the absence of conjugate points on the geodesics.
For two manifolds of the same constant negative curvature and the same dimension 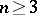 , isomorphism of their
, isomorphism of their 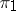 's implies isometry (Mostow's rigidity theorem).
's implies isometry (Mostow's rigidity theorem).
Riemannian manifolds for which 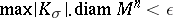 are called
are called  -flat. For an arbitrary
-flat. For an arbitrary 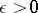 such manifolds can be topologically different from locally flat manifolds. For them, for any
such manifolds can be topologically different from locally flat manifolds. For them, for any 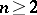 , there is an
, there is an 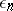 such that for an
such that for an 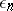 -flat
-flat 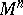 there is a nilpotent subgroup of finite index in
there is a nilpotent subgroup of finite index in 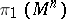 . In this case
. In this case 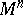 permits a finite (with multiplicity dependent only on
permits a finite (with multiplicity dependent only on 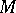 ) covering diffeomorphic to the quotient space of a nilpotent Lie group by a discrete subgroup of it (see [8]).
) covering diffeomorphic to the quotient space of a nilpotent Lie group by a discrete subgroup of it (see [8]).
A complete Riemannian manifold with curvature 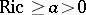 has finite
has finite 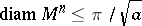 and thus a finite group
and thus a finite group 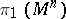 . If
. If 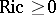 for a closed
for a closed 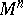 , there is a finite normal subgroup
, there is a finite normal subgroup 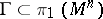 such that
such that 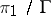 is a discrete group of isometries of
is a discrete group of isometries of 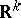 ,
, 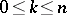 ; moreover,
; moreover, 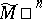 decomposes into the direct metric product
decomposes into the direct metric product 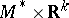 , where
, where  is closed, the decomposition is invariant relative to
is closed, the decomposition is invariant relative to 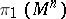 and
and 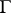 is trivial in
is trivial in 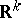 .
.
In addition to the study of  , several estimates of the Betti numbers
, several estimates of the Betti numbers 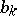 have been made using the theory of harmonic differential forms for
have been made using the theory of harmonic differential forms for 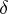 -pinched
-pinched 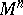 . Thus,
. Thus, 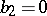 when
when 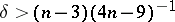 and
and 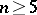 is odd.
is odd.
Comparison theorems.
Many global properties of Riemannian manifolds are proved by comparing the structures in the Riemannian manifolds under consideration to similar structures on a standard space. This usually is a manifold of constant curvature, or, more rarely, another symmetric space. Below, a  -plane is
-plane is  when
when 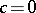 , the sphere
, the sphere 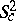 of radius
of radius 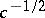 when
when 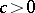 and the Lobachevskii plane of curvature
and the Lobachevskii plane of curvature  when
when 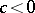 .
.
The Toponogov theorem on the comparison of angles has many applications: In a Riemannian manifold 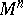 , let all
, let all 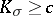 , let
, let 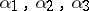 be the angles of a triangle made of shortest curves, and let
be the angles of a triangle made of shortest curves, and let 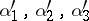 be the corresponding angles of a triangle with sides of the same length in the
be the corresponding angles of a triangle with sides of the same length in the  -plane; then
-plane; then 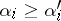 . If
. If 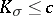 and if any two points of the sides of the triangle in
and if any two points of the sides of the triangle in 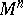 in question can be joined by a single shortest curve, then
in question can be joined by a single shortest curve, then 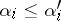 . This theorem is equivalent to the following convexity condition: If in
. This theorem is equivalent to the following convexity condition: If in 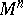 the shortest curves
the shortest curves 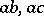 form the same angle as the shortest curves
form the same angle as the shortest curves 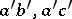 of the same length in the
of the same length in the  -plane, then
-plane, then 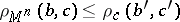 . What is being compared here is essentially the rate of divergence of the shortest curves.
. What is being compared here is essentially the rate of divergence of the shortest curves.
Rauch's comparison theorem compares the rate of movement of the end points 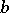 and
and 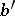 of two shortest curves
of two shortest curves 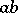 ,
, 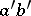 in two Riemannian manifolds
in two Riemannian manifolds 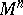 and
and 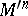 when
when 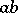 and
and 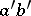 turn around their origins
turn around their origins  ,
, 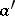 with the same rate, under conditions when (in a natural comparison) the sectional curvatures in
with the same rate, under conditions when (in a natural comparison) the sectional curvatures in 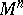 are not less than in
are not less than in 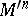 . Then the rate of movement of
. Then the rate of movement of 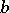 is not greater than the rate of
is not greater than the rate of 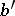 . In the fundamental case (comparison with a
. In the fundamental case (comparison with a  -plane), Rauch's theorem is equivalent to the infinitesimal version of the theorem on the comparison of angles.
-plane), Rauch's theorem is equivalent to the infinitesimal version of the theorem on the comparison of angles.
There are theorems similar to Rauch's in which the points  ,
, 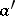 move on hypersurfaces to which
move on hypersurfaces to which 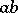 ,
, 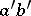 remain orthogonal. There are also comparison theorems for volumes of tubular neighbourhoods of submanifolds (see [13], [16]).
remain orthogonal. There are also comparison theorems for volumes of tubular neighbourhoods of submanifolds (see [13], [16]).
Extremal theorems.
Comparison theorems lead to estimates of such characteristics of 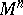 as the diameter, the radius of injectivity, the length of a closed geodesic, the volume of a sphere of given radius, etc. Extremal theorems give answers to questions concerning cases of achieving equality in such estimates.
as the diameter, the radius of injectivity, the length of a closed geodesic, the volume of a sphere of given radius, etc. Extremal theorems give answers to questions concerning cases of achieving equality in such estimates.
For 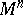 with
with 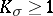 one always has
one always has 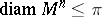 . Equality is achieved only for the unit sphere. If
. Equality is achieved only for the unit sphere. If 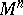 is closed and
is closed and 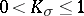 when
when  is even or
is even or 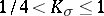 when
when  is odd, then the radius of injectivity
is odd, then the radius of injectivity 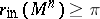 and the length of a closed geodesic
and the length of a closed geodesic 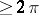 . If in this case there is a closed geodesic
. If in this case there is a closed geodesic 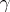 of length
of length 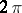 in
in 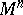 , then, if
, then, if  is even, there is a totally geodesic surface in
is even, there is a totally geodesic surface in 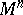 which contains
which contains 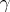 and which is isometric to
and which is isometric to 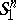 , while if
, while if 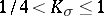 , independently of the parity of
, independently of the parity of  ,
, 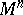 is isometric to
is isometric to 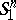 (see [6]). The volume of a sphere
(see [6]). The volume of a sphere 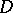 of radius
of radius  in an
in an 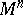 with
with 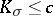
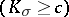 is not less (not greater) than the volume of the sphere
is not less (not greater) than the volume of the sphere 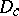 of the same radius in the space of constant curvature
of the same radius in the space of constant curvature  , with equality only if
, with equality only if 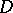 is isometric to
is isometric to 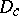 .
.
Extremal theorems are not always connected with estimates of the curvature. For example, for any point in a closed surface 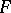 , let the set of points conjugate to it consist of a single point. Then
, let the set of points conjugate to it consist of a single point. Then 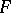 is isometric to a sphere.
is isometric to a sphere.
Finiteness of topological types.
Among the closed Riemannian manifolds with uniformly bounded curvatures and radii of injectivity bounded from below, 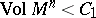 ,
, 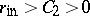 ,
, 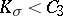 , only finitely many are homotopically pairwise non-equivalent, and if
, only finitely many are homotopically pairwise non-equivalent, and if 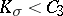 is changed into
is changed into 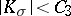 , only finitely many of them are pairwise non-homeomorphic. In this statement the condition
, only finitely many of them are pairwise non-homeomorphic. In this statement the condition 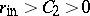 can be replaced by the conditions
can be replaced by the conditions 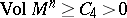 ,
, 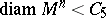 , which imply it but are more easily verifiable (see [14]).
, which imply it but are more easily verifiable (see [14]).
For a Riemannian manifold with 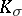 of fixed sign, the conditions that guarantee the finiteness of its topological type are simplified. For example, for even
of fixed sign, the conditions that guarantee the finiteness of its topological type are simplified. For example, for even  and
and 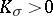 the condition
the condition 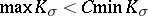 is sufficient.
is sufficient.
When 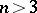 , for
, for 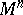 with
with 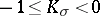 the estimate
the estimate 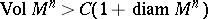 is true. Therefore, when
is true. Therefore, when 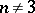 , the number of topological types of closed Riemannian manifolds that satisfy the conditions
, the number of topological types of closed Riemannian manifolds that satisfy the conditions 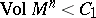 ,
, 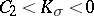 , is finite. But when
, is finite. But when 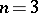 , there is an infinite number of pairwise non-homeomorphic
, there is an infinite number of pairwise non-homeomorphic 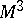 satisfying these conditions (see [12]).
satisfying these conditions (see [12]).
Metrics with prescribed curvature.
Let 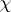 be the Euler characteristic of a closed surface
be the Euler characteristic of a closed surface 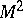 . In order that a smooth function
. In order that a smooth function 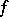 on
on 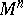 be the curvature of a Riemannian metric in
be the curvature of a Riemannian metric in 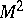 it is necessary that
it is necessary that 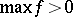 when
when  ,
, 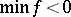 when
when 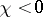 and
and 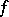 changes sign or
changes sign or 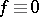 when
when 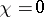 . These conditions are also sufficient. The condition
. These conditions are also sufficient. The condition 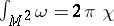 is necessary and sufficient for the
is necessary and sufficient for the  -form
-form  to be the curvature form
to be the curvature form  of a Riemannian metric in
of a Riemannian metric in  . If
. If  is an open submanifold of a closed manifold
is an open submanifold of a closed manifold 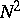 , then any smooth
, then any smooth 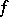 on
on 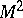 is the curvature of a (possibly incomplete) Riemannian metric in
is the curvature of a (possibly incomplete) Riemannian metric in  . Necessary and sufficient conditions under which
. Necessary and sufficient conditions under which 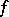 is the curvature of a complete Riemannian metric in a non-compact surface have been ascertained for finitely-connected surfaces.
is the curvature of a complete Riemannian metric in a non-compact surface have been ascertained for finitely-connected surfaces.
As the dimension increases, the number of independent components of the curvature tensor increases faster than the number of components of the metric tensor. The conditions under which the given tensor field is, at least locally, the field of the curvature tensor of a certain metric are unknown (1991). But for the scalar curvature, when 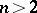 , each smooth function
, each smooth function 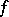 on a closed
on a closed 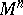 for which
for which 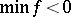 is the scalar curvature of a Riemannian metric in
is the scalar curvature of a Riemannian metric in 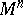 (see [4]). There are manifolds which do not permit a metric with a positive scalar curvature, as is the case with a three-dimensional torus (see [5]).
(see [4]). There are manifolds which do not permit a metric with a positive scalar curvature, as is the case with a three-dimensional torus (see [5]).
Convex functions.
The existence of a scalar function 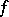 on a Riemannian manifold
on a Riemannian manifold 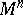 that is convex along any geodesic imposes strict limitations on the structure of such an
that is convex along any geodesic imposes strict limitations on the structure of such an 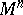 . For example, if there is a convex function
. For example, if there is a convex function 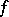 on
on 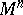 , then
, then 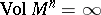 . If
. If 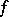 is strictly convex and if for any
is strictly convex and if for any  the sets
the sets 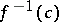 are compact, then
are compact, then 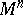 is diffeomorphic to
is diffeomorphic to 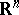 .
.
Convex functions can be constructed in a number of cases. For example, when 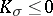 , the functions
, the functions 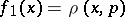 ,
, 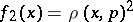 ,
, 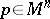 , are convex. If
, are convex. If 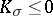 and
and 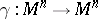 is an isometry, then the function
is an isometry, then the function 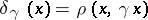 is convex. When
is convex. When  , there are convex
, there are convex  with compact
with compact 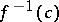 ; this is connected with the absolute convexity (when
; this is connected with the absolute convexity (when 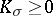 ) of the complements to horospheres and with the fact that if
) of the complements to horospheres and with the fact that if 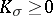 , then the convexity of a set
, then the convexity of a set 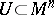 implies the convexity of the set
implies the convexity of the set 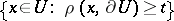 .
.
Problems of Riemannian geometry in the large have also been studied for Riemannian manifolds with additional structures, such as for Kähler manifolds (see [10]).
References
| [1] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
| [2] | Yu.D. Burago, V.A. Zalgaller, "Convex sets in Riemannian spaces of non-negative curvature" Russian Math. Surveys , 32 : 3 (1977) pp. 1–57 Uspekhi Mat. Nauk , 32 : 3 (1977) pp. 3–55 |
| [3] | J. Cheeger, D.G. Ebin, "Comparison theorems in Riemannian geometry" , North-Holland (1975) |
| [4] | , Research on the metric theory of surfaces , Moscow (1980) (In Russian; translated from English and French) |
| [5] | R. Schoen, S.-T. Yau, "Existence of incompressible minimal surfaces and the topology of three-dimensional manifolds with non-negative scalar curvature" Ann. of Math. , 110 (1979) pp. 127–142 |
| [6] | V.A. Toponogov, "Extremal theorems for Riemann spaces with curvature bounded above I" Sib. Math. J. , 15 : 6 (1974) pp. 954–971 Sibirsk. Mat. Zh. , 15 : 6 (1974) pp. 1348–1371 |
| [7] | M. Gromov, H.B., jr. Lawson, "Spin and scalar curvature in the presence of a fundamental group I" Ann. of Math. , 111 : 2 (1980) pp. 209–230 |
| [8] | P. Buser, H. Karcher, "Gromov's almost flat manifolds" Astérique , 81 (1981) |
| [9] | J.A. Wolf, "Spaces of constant curvature" , Publish or Perish (1977) |
| [10] | S.I. Goldberg, "Curvature and homology" , Acad. Press (1962) |
| [11] | A.L. Besse, "Manifolds all of whose geodesics are closed" , Springer (1978) |
| [12] | W. Thurston, "The geometry and topology of 3-manifolds" , Princeton Univ. Press (1978) (Preprint) |
| [13] | E. Heintze, H. Karcher, "A general comparison theorem with applications to volume estimates for submanifolds" Ann. Sci. Ecole Norm. Sup. , 11 : 4 (1978) pp. 451–470 |
| [14] | J. Cheeger, "Pinching theorems for a certain class of Riemannian manifolds" Amer. J. Math. , 91 : 3 (1969) pp. 807–834 |
| [15] | Min-Do, E. Ruh, "Comparison theorems for compact symmetric spaces" Ann. Sci. Ecole Norm. Sup. , 12 (1979) pp. 335–353 |
| [16] | A. Gray, "Comparison theorems for the volumes of tubes as generalizations of the Weyl tube formula" Topology , 21 : 2 (1982) pp. 201–228 |
Comments
For some more results on the interrelations between curvature and fundamental group cf. (the editorial comments to) Polycyclic group and Polynomial and exponential growth in groups and algebras.
Let 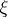 be a unit length tangent vector at
be a unit length tangent vector at 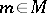 . Let
. Let 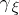 be its geodesic. For sufficiently small
be its geodesic. For sufficiently small 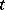 the distance between the starting point
the distance between the starting point 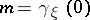 and
and 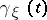 is
is 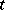 , but this may fail for larger
, but this may fail for larger 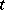 . The cut value function (on the sphere subbundle of the tangent bundle) is defined by
. The cut value function (on the sphere subbundle of the tangent bundle) is defined by
 |
The cut locus of 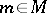 is by definition the set of points
is by definition the set of points 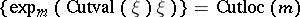 , where
, where 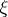 runs over all unit length tangent vectors at
runs over all unit length tangent vectors at 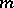 and
and 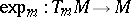 is the exponential mapping at
is the exponential mapping at 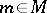 ; cf. Exponential mapping and the subsection "Exponential mapping" in Riemannian geometry.
; cf. Exponential mapping and the subsection "Exponential mapping" in Riemannian geometry.
The radius of injectivity, 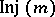 , at
, at 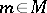 is defined as
is defined as 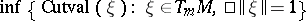 , and the global radius of injectivity of
, and the global radius of injectivity of 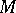 is
is  . It is always positive if
. It is always positive if 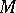 is compact, but can be zero if
is compact, but can be zero if 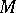 is non-compact.
is non-compact.
The cut locus was introduced by H. Poincaré under the name "ligne de partage" . Every compact surface admits a Riemannian metric of constant curvature. "Cutting up" a higher-genus surface 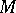 along a cut locus yields a particularly nice representation of
along a cut locus yields a particularly nice representation of  as a domain bounded by a polygon on which edges are pairwise identified, [a3]. For the sphere, the genus 0 case, the cut locus of a point is the single diametrically-opposite point.
as a domain bounded by a polygon on which edges are pairwise identified, [a3]. For the sphere, the genus 0 case, the cut locus of a point is the single diametrically-opposite point.
References
| [a1] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) pp. Sect. 11.4 (Translated from French) |
| [a2] | W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) pp. Chapt. 2 (Translated from German) |
| [a3] | S. Gallot, D. Hulin, J. Lafontaine, "Riemannian geometry" , Springer (1987) (Translated from French) |
| [a4] | W.M. Boothby, "An introduction to differentiable manifolds and Riemannian geometry" , Acad. Press (1975) |
| [a5] | W. Greub, S. Halperin, R. Vanstone, "Connections, curvature, and cohomology" , 1–3 , Acad. Press (1972–1976) |
Riemannian geometry in the large. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemannian_geometry_in_the_large&oldid=48559