|
|
| Line 1: |
Line 1: |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w0980601.png" /> be a field of characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w0980602.png" />. Consider the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w0980603.png" />-algebra
| + | <!-- |
| | + | w0980601.png |
| | + | $#A+1 = 67 n = 1 |
| | + | $#C+1 = 67 : ~/encyclopedia/old_files/data/W098/W.0908060 Witt algebra |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w0980604.png" /></td> </tr></table>
| + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w0980605.png" /> be the algebra of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w0980606.png" />-derivations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w0980607.png" />. The algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w0980608.png" /> is known as the Witt algebra. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w0980609.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806010.png" />) are known as the split Jacobson–Witt algebras. The algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806011.png" /> is a simple [[Lie algebra|Lie algebra]], except when it is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806012.png" />-dimensional. The dimension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806013.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806014.png" />. | + | Let $ k $ |
| | + | be a field of characteristic $ p \neq 0 $. |
| | + | Consider the $ k $- |
| | + | algebra |
| | | | |
| − | More generally one considers the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806015.png" />-algebras
| + | $$ |
| | + | A _ {n} = k [ X _ {1} \dots X _ {n} ] / |
| | + | ( X _ {1} ^ {p} \dots X _ {n} ^ {p} ) . |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806016.png" /></td> </tr></table>
| + | Let $ V _ {n} $ |
| | + | be the algebra of $ k $- |
| | + | derivations of $ A _ {n} $. |
| | + | The algebra $ V _ {1} $ |
| | + | is known as the Witt algebra. The $ V _ {n} $( |
| | + | $ n \geq 2 $) |
| | + | are known as the split Jacobson–Witt algebras. The algebra $ V _ {n} $ |
| | + | is a simple [[Lie algebra|Lie algebra]], except when it is $ 2 $- |
| | + | dimensional. The dimension of $ V _ {n} $ |
| | + | is $ np ^ {n} $. |
| | | | |
| − | and their algebras of derivations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806017.png" />, the Jacobson–Witt algebras. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806019.png" /> are (obviously) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806020.png" />-forms of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806021.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806022.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806023.png" /> (cf. [[Form of an (algebraic) structure|Form of an (algebraic) structure]]). Many simple Lie algebras in characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806024.png" /> arise as subalgebras of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806025.png" />.
| + | More generally one considers the $ k $- |
| | + | algebras |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806026.png" /> be an additive group of functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806027.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806028.png" /> such that the only element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806029.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806030.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806031.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806032.png" /> is the zero element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806033.png" />. For instance, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806034.png" /> can be the set of all functions from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806035.png" /> to some additive subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806036.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806037.png" /> is finite, it is of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806038.png" /> for some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806039.png" />. Now, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806040.png" /> be a [[Vector space|vector space]] over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806041.png" /> with basis elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806042.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806043.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806044.png" />, and define a bilinear product on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806045.png" /> by
| + | $$ |
| | + | A _ {n} ( \xi ) = k [ X _ {1} \dots X _ {n} ] / |
| | + | ( X _ {1} ^ {p} - \xi _ {1} \dots X _ {n} ^ {p} - \xi _ {n} ) , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806046.png" /></td> </tr></table>
| + | and their algebras of derivations $ V _ {n} ( \xi ) $, |
| | + | the Jacobson–Witt algebras. The $ A _ {n} ( \xi ) $ |
| | + | and $ V _ {n} ( \xi ) $ |
| | + | are (obviously) $ k ^ \prime / k $- |
| | + | forms of $ A _ {n} $ |
| | + | and $ V _ {n} $, |
| | + | where $ k ^ \prime = k ( \xi _ {1} ^ {1/p} \dots \xi _ {n} ^ {1/p} ) $( |
| | + | cf. [[Form of an (algebraic) structure|Form of an (algebraic) structure]]). Many simple Lie algebras in characteristic $ p $ |
| | + | arise as subalgebras of the $ V _ {n} $. |
| | | | |
| − | There results a Lie algebra, called a generalized Witt algebra. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806047.png" /> is finite of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806048.png" />, the dimension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806049.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806050.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806051.png" /> is a simple Lie algebra if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806052.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806053.png" />.
| + | Let $ G $ |
| | + | be an additive group of functions on $ \{ 1 \dots m \} $ |
| | + | into $ k $ |
| | + | such that the only element $ f $ |
| | + | of $ G $ |
| | + | such that $ \sum f( i) g( i) = 0 $ |
| | + | for all $ g \in G $ |
| | + | is the zero element $ f = 0 $. |
| | + | For instance, $ G $ |
| | + | can be the set of all functions from $ \{ 1 \dots m \} $ |
| | + | to some additive subgroup of $ k $. |
| | + | If $ G $ |
| | + | is finite, it is of order $ p ^ {n} $ |
| | + | for some $ n $. |
| | + | Now, let $ V $ |
| | + | be a [[Vector space|vector space]] over $ k $ |
| | + | with basis elements $ e _ {g} ^ {i} $, |
| | + | $ i = 1 \dots m $, |
| | + | $ g \in G $, |
| | + | and define a bilinear product on $ V $ |
| | + | by |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806054.png" /> is of characteristic zero, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806055.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806056.png" /> is the additive subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806057.png" />, the same construction results in the [[Virasoro algebra|Virasoro algebra]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806058.png" />.
| + | $$ |
| | + | [ e _ {g} ^ {i} , e _ {h} ^ {j} ] = \ |
| | + | h( i) e _ {g+ h } ^ {j} - |
| | + | g( j) e _ {g+ h } ^ {i} . |
| | + | $$ |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806059.png" /> is of characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806060.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806061.png" /> is the group of all functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806062.png" /> with values in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806063.png" />, one recovers the Jacobson–Witt algebras <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806064.png" />. | + | There results a Lie algebra, called a generalized Witt algebra. If $ G $ |
| | + | is finite of order $ p ^ {n} $, |
| | + | the dimension of $ V $ |
| | + | is $ m p ^ {n} $, |
| | + | and $ V $ |
| | + | is a simple Lie algebra if $ m > 1 $ |
| | + | or $ p > 2 $. |
| | | | |
| − | There are no isomorphisms between the Jacobson–Witt algebras <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806065.png" /> and the classical Lie algebras in positive characteristic when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806066.png" />. Several more classes of simple Lie algebras different from the classical ones and the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806067.png" /> are known, [[#References|[a1]]]. | + | If $ k $ |
| | + | is of characteristic zero, $ m = 1 $ |
| | + | and $ G $ |
| | + | is the additive subgroup $ \mathbf Z \subset k $, |
| | + | the same construction results in the [[Virasoro algebra|Virasoro algebra]] $ [ e _ {g} , e _ {h} ] = ( h- g) e _ {g+} h $. |
| | + | |
| | + | If $ k $ |
| | + | is of characteristic $ p $ |
| | + | and $ G $ |
| | + | is the group of all functions on $ \{ 1 \dots n \} $ |
| | + | with values in $ \mathbf Z / ( p) \subset k $, |
| | + | one recovers the Jacobson–Witt algebras $ V _ {n} $. |
| | + | |
| | + | There are no isomorphisms between the Jacobson–Witt algebras $ V _ {n} $ |
| | + | and the classical Lie algebras in positive characteristic when $ \mathop{\rm char} ( k) \neq 2, 3 $. |
| | + | Several more classes of simple Lie algebras different from the classical ones and the $ V _ {n} $ |
| | + | are known, [[#References|[a1]]]. |
| | | | |
| | The Witt algebra(s) described here should of course not be confused with the [[Witt ring|Witt ring]] of quadratic forms over a field, nor with the various rings of Witt vectors, cf. [[Witt vector|Witt vector]]. | | The Witt algebra(s) described here should of course not be confused with the [[Witt ring|Witt ring]] of quadratic forms over a field, nor with the various rings of Witt vectors, cf. [[Witt vector|Witt vector]]. |
Let $ k $
be a field of characteristic $ p \neq 0 $.
Consider the $ k $-
algebra
$$
A _ {n} = k [ X _ {1} \dots X _ {n} ] /
( X _ {1} ^ {p} \dots X _ {n} ^ {p} ) .
$$
Let $ V _ {n} $
be the algebra of $ k $-
derivations of $ A _ {n} $.
The algebra $ V _ {1} $
is known as the Witt algebra. The $ V _ {n} $(
$ n \geq 2 $)
are known as the split Jacobson–Witt algebras. The algebra $ V _ {n} $
is a simple Lie algebra, except when it is $ 2 $-
dimensional. The dimension of $ V _ {n} $
is $ np ^ {n} $.
More generally one considers the $ k $-
algebras
$$
A _ {n} ( \xi ) = k [ X _ {1} \dots X _ {n} ] /
( X _ {1} ^ {p} - \xi _ {1} \dots X _ {n} ^ {p} - \xi _ {n} ) ,
$$
and their algebras of derivations $ V _ {n} ( \xi ) $,
the Jacobson–Witt algebras. The $ A _ {n} ( \xi ) $
and $ V _ {n} ( \xi ) $
are (obviously) $ k ^ \prime / k $-
forms of $ A _ {n} $
and $ V _ {n} $,
where $ k ^ \prime = k ( \xi _ {1} ^ {1/p} \dots \xi _ {n} ^ {1/p} ) $(
cf. Form of an (algebraic) structure). Many simple Lie algebras in characteristic $ p $
arise as subalgebras of the $ V _ {n} $.
Let $ G $
be an additive group of functions on $ \{ 1 \dots m \} $
into $ k $
such that the only element $ f $
of $ G $
such that $ \sum f( i) g( i) = 0 $
for all $ g \in G $
is the zero element $ f = 0 $.
For instance, $ G $
can be the set of all functions from $ \{ 1 \dots m \} $
to some additive subgroup of $ k $.
If $ G $
is finite, it is of order $ p ^ {n} $
for some $ n $.
Now, let $ V $
be a vector space over $ k $
with basis elements $ e _ {g} ^ {i} $,
$ i = 1 \dots m $,
$ g \in G $,
and define a bilinear product on $ V $
by
$$
[ e _ {g} ^ {i} , e _ {h} ^ {j} ] = \
h( i) e _ {g+ h } ^ {j} -
g( j) e _ {g+ h } ^ {i} .
$$
There results a Lie algebra, called a generalized Witt algebra. If $ G $
is finite of order $ p ^ {n} $,
the dimension of $ V $
is $ m p ^ {n} $,
and $ V $
is a simple Lie algebra if $ m > 1 $
or $ p > 2 $.
If $ k $
is of characteristic zero, $ m = 1 $
and $ G $
is the additive subgroup $ \mathbf Z \subset k $,
the same construction results in the Virasoro algebra $ [ e _ {g} , e _ {h} ] = ( h- g) e _ {g+} h $.
If $ k $
is of characteristic $ p $
and $ G $
is the group of all functions on $ \{ 1 \dots n \} $
with values in $ \mathbf Z / ( p) \subset k $,
one recovers the Jacobson–Witt algebras $ V _ {n} $.
There are no isomorphisms between the Jacobson–Witt algebras $ V _ {n} $
and the classical Lie algebras in positive characteristic when $ \mathop{\rm char} ( k) \neq 2, 3 $.
Several more classes of simple Lie algebras different from the classical ones and the $ V _ {n} $
are known, [a1].
The Witt algebra(s) described here should of course not be confused with the Witt ring of quadratic forms over a field, nor with the various rings of Witt vectors, cf. Witt vector.
References
| [a1] | G.B. Seligman, "Modular Lie algebras" , Springer (1967) MR0245627 Zbl 0189.03201 |
| [a2] | N. Jacobson, "Classes of restricted Lie algebras of characteristic 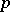 , II" Duke Math. J. , 10 (1943) pp. 107–121 , II" Duke Math. J. , 10 (1943) pp. 107–121 |
| [a3] | R. Ree, "On generalised Witt algebras" Trans. Amer. Math. Soc. , 83 (1956) pp. 510–546 |
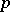 , II" Duke Math. J. , 10 (1943) pp. 107–121
, II" Duke Math. J. , 10 (1943) pp. 107–121