Difference between revisions of "Series of representations"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | s0846801.png | ||
| + | $#A+1 = 0 n = 2 | ||
| + | $#C+1 = 0 : ~/encyclopedia/old_files/data/S084/S.0804680 Series of representations | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
Families of (continuous, irreducible, unitary) representations of a locally compact group (more precisely, sets of unitary equivalence classes of irreducible representations, cf. [[Irreducible representation|Irreducible representation]]; [[Representation of a compact group|Representation of a compact group]]) that have common properties relative to the [[Regular representation|regular representation]] of the group. Thus, the family of irreducible unitary representations of a group whose matrix entries are uniform limits on compact sets of matrix entries of the regular representation form the principal series representations; the remaining irreducible unitary representations (if they exist) form the complementary series representations; and the family (of equivalence classes) of irreducible direct summands of the regular representation forms the discrete series representations of the given group. For reductive Lie groups or Chevalley groups, the concept of a series of representations is also meaningful for subsets of the set of equivalence classes of representations of the group whose elements have some properties relative to the regular representation of the reductive quotient groups by the parabolic subgroups of this group. The family of representations of a reductive group that are induced by the finite-dimensional representations of its parabolic subgroup forms part of the representation space related to this parabolic subgroup; this part is called the corresponding principal (principal degenerate, if the parabolic subgroup is not a Borel subgroup) series representations. | Families of (continuous, irreducible, unitary) representations of a locally compact group (more precisely, sets of unitary equivalence classes of irreducible representations, cf. [[Irreducible representation|Irreducible representation]]; [[Representation of a compact group|Representation of a compact group]]) that have common properties relative to the [[Regular representation|regular representation]] of the group. Thus, the family of irreducible unitary representations of a group whose matrix entries are uniform limits on compact sets of matrix entries of the regular representation form the principal series representations; the remaining irreducible unitary representations (if they exist) form the complementary series representations; and the family (of equivalence classes) of irreducible direct summands of the regular representation forms the discrete series representations of the given group. For reductive Lie groups or Chevalley groups, the concept of a series of representations is also meaningful for subsets of the set of equivalence classes of representations of the group whose elements have some properties relative to the regular representation of the reductive quotient groups by the parabolic subgroups of this group. The family of representations of a reductive group that are induced by the finite-dimensional representations of its parabolic subgroup forms part of the representation space related to this parabolic subgroup; this part is called the corresponding principal (principal degenerate, if the parabolic subgroup is not a Borel subgroup) series representations. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> Nguyen Hu'u Anh, "Classification of connected unimodular Lie groups with discrete series" ''Ann. Inst. Fourier'' , '''30''' : 1 (1980) pp. 159–192</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Cailliz, "Les sous-groupes paraboliques de <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084680/s0846801.png" /> et <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084680/s0846802.png" /> et applications à l'Aeetude des réprésentations" J. Oberdörfer (ed.) , ''Anal. Harmonique sur les Groupes de Lie (Sem. Nancy-Strassbourg, 1976–1978) II'' , ''Lect. notes in math.'' , '''739''' , Springer (1979) pp. 51–106</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> Nguyen Hu'u Anh, "Classification of connected unimodular Lie groups with discrete series" ''Ann. Inst. Fourier'' , '''30''' : 1 (1980) pp. 159–192</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Cailliz, "Les sous-groupes paraboliques de <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084680/s0846801.png" /> et <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084680/s0846802.png" /> et applications à l'Aeetude des réprésentations" J. Oberdörfer (ed.) , ''Anal. Harmonique sur les Groupes de Lie (Sem. Nancy-Strassbourg, 1976–1978) II'' , ''Lect. notes in math.'' , '''739''' , Springer (1979) pp. 51–106</TD></TR></table> | ||
Revision as of 08:13, 6 June 2020
Families of (continuous, irreducible, unitary) representations of a locally compact group (more precisely, sets of unitary equivalence classes of irreducible representations, cf. Irreducible representation; Representation of a compact group) that have common properties relative to the regular representation of the group. Thus, the family of irreducible unitary representations of a group whose matrix entries are uniform limits on compact sets of matrix entries of the regular representation form the principal series representations; the remaining irreducible unitary representations (if they exist) form the complementary series representations; and the family (of equivalence classes) of irreducible direct summands of the regular representation forms the discrete series representations of the given group. For reductive Lie groups or Chevalley groups, the concept of a series of representations is also meaningful for subsets of the set of equivalence classes of representations of the group whose elements have some properties relative to the regular representation of the reductive quotient groups by the parabolic subgroups of this group. The family of representations of a reductive group that are induced by the finite-dimensional representations of its parabolic subgroup forms part of the representation space related to this parabolic subgroup; this part is called the corresponding principal (principal degenerate, if the parabolic subgroup is not a Borel subgroup) series representations.
References
| [1] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [2] | Nguyen Hu'u Anh, "Classification of connected unimodular Lie groups with discrete series" Ann. Inst. Fourier , 30 : 1 (1980) pp. 159–192 |
| [3] | J. Cailliz, "Les sous-groupes paraboliques de 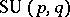 et 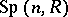 et applications à l'Aeetude des réprésentations" J. Oberdörfer (ed.) , Anal. Harmonique sur les Groupes de Lie (Sem. Nancy-Strassbourg, 1976–1978) II , Lect. notes in math. , 739 , Springer (1979) pp. 51–106 |
How to Cite This Entry:
Series of representations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Series_of_representations&oldid=14345
Series of representations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Series_of_representations&oldid=14345
This article was adapted from an original article by A.I. Shtern (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article