Difference between revisions of "Riemannian space, generalized"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | r0822001.png | ||
| + | $#A+1 = 293 n = 4 | ||
| + | $#C+1 = 293 : ~/encyclopedia/old_files/data/R082/R.0802200 Riemannian space, generalized | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
A space with an [[Internal metric|internal metric]] subject to certain restrictions on the curvature. Spaces of "bounded curvature from above" and others belong to this class (see [[#References|[3]]]). Generalized Riemannian spaces differ from Riemannian spaces (cf. [[Riemannian space|Riemannian space]]) not only by greater generality but also by the fact that they are defined and studied on the basis of their metric alone, without coordinates. Under a certain combination of conditions concerning the curvature and the behaviour of shortests curves (i.e. curves whose lengths are equal to the distances between the end points), a generalized Riemannian space turns out to be Riemannian, which gives a purely metric definition of a Riemannian space. | A space with an [[Internal metric|internal metric]] subject to certain restrictions on the curvature. Spaces of "bounded curvature from above" and others belong to this class (see [[#References|[3]]]). Generalized Riemannian spaces differ from Riemannian spaces (cf. [[Riemannian space|Riemannian space]]) not only by greater generality but also by the fact that they are defined and studied on the basis of their metric alone, without coordinates. Under a certain combination of conditions concerning the curvature and the behaviour of shortests curves (i.e. curves whose lengths are equal to the distances between the end points), a generalized Riemannian space turns out to be Riemannian, which gives a purely metric definition of a Riemannian space. | ||
| − | Definitions of generalized Riemannian spaces are based on the classical relation between the curvature and the excess of a [[Geodesic triangle|geodesic triangle]] (excess | + | Definitions of generalized Riemannian spaces are based on the classical relation between the curvature and the excess of a [[Geodesic triangle|geodesic triangle]] (excess $ = $ |
| + | sum of the angles minus $ \pi $). | ||
| + | These concepts are carried over to a space with an internal metric, such that each point of it has a neighbourhood in which any two points can be connected by a shortest curve. This condition is assumed hereafter without further stipulation. A triangle $ T = ABC $ | ||
| + | is triplet of shortests curves $ AB, BC, CA $— | ||
| + | the sides of the triangle — connecting in pairs three different points $ A, B, C $— | ||
| + | the vertices of the triangle. The angle between curves can be defined in any metric space: Let $ L, M $ | ||
| + | be curves starting at the same point $ O $ | ||
| + | in a space with metric $ \rho $. | ||
| + | One chooses points $ X \in L $, | ||
| + | $ Y \in M $ | ||
| + | $ ( X, Y \neq O) $ | ||
| + | and constructs the Euclidean triangle with sides $ x = \rho ( O, X) $, | ||
| + | $ y = \rho ( O, Y) $, | ||
| + | $ z = \rho ( X, Y) $ | ||
| + | and angle $ \gamma ( x, y) $ | ||
| + | opposite to the side $ z $. | ||
| + | One defines the upper angle between $ L $ | ||
| + | and $ M $ | ||
| + | as: | ||
| − | + | $$ \tag{1 } | |
| + | \overline \alpha \; = \overline{\lim\limits}\; _ {x,y \rightarrow 0 } \gamma ( x, y). | ||
| + | $$ | ||
| − | The upper angles of the triangle are the upper angles | + | The upper angles of the triangle are the upper angles $ \widetilde \alpha , \widetilde \beta , \widetilde \gamma $ |
| + | between its sides at the vertices $ A, B, C $ | ||
| + | and the excess of the triangle is $ \overline \delta \; ( T) = \widetilde \alpha + \widetilde \beta + \widetilde \gamma - \pi $. | ||
| − | A generalized Riemannian space of bounded curvature ( | + | A generalized Riemannian space of bounded curvature ( $ \leq K $ |
| + | and $ \geq K ^ \prime $) | ||
| + | is defined by the following condition: | ||
| − | + | $ A $) | |
| + | for any sequence of triangles $ T _ {n} $ | ||
| + | contracting to a point, | ||
| − | + | $$ \tag{2 } | |
| + | K \geq \overline{\lim\limits}\; | ||
| + | \frac{\overline \delta \; ( T _ {n} ) }{\sigma ( T _ {n} ^ {0} ) } | ||
| + | \geq | ||
| + | fnnme \underline{lim} | ||
| + | \frac{\overline \delta \; ( T _ {n} ) }{\sigma ( T _ {n} ^ {0} ) } | ||
| + | \geq K ^ \prime , | ||
| + | $$ | ||
| − | where | + | where $ \sigma ( T _ {n} ^ {0} ) $ |
| + | is the area of the Euclidean triangle with the same sides as $ T _ {n} $( | ||
| + | if $ \sigma ( T _ {n} ^ {0} ) = 0 $, | ||
| + | then $ \overline \delta \; ( T _ {n} ) = 0 $). | ||
| + | Such a space turns out to be Riemannian under two natural additional conditions: | ||
1) local compactness of the space (in a space with an internal metric this already ensures the condition of local existence of shortests); | 1) local compactness of the space (in a space with an internal metric this already ensures the condition of local existence of shortests); | ||
| − | 2) local extendibility of shortests, i.e. each point has a neighbourhood | + | 2) local extendibility of shortests, i.e. each point has a neighbourhood $ U $ |
| + | such that any shortest $ XY $, | ||
| + | where $ X, Y \in U $, | ||
| + | can be extended beyond its end points. Under all these conditions the space is Riemannian (see [[#References|[4]]]); moreover, in a neighbourhood of each point one can introduce coordinates $ x ^ {i} $ | ||
| + | so that the metric will be given by a line element $ ds ^ {2} = g _ {ij} dx ^ {i} dx ^ {j} $ | ||
| + | with coefficients $ g _ {ij} \in W _ {q} ^ {2} \cap C ^ {1, \alpha } $, | ||
| + | $ 0 < \alpha < 1 $. | ||
| + | Thus, a [[Parallel displacement(2)|parallel displacement]] is given (with continuous $ \Gamma _ {jk} ^ {i} $) | ||
| + | and, almost everywhere, a [[Curvature tensor|curvature tensor]] (see [[#References|[9]]]). | ||
| − | Moreover, it has been proved [[#References|[9]]] that the coordinates | + | Moreover, it has been proved [[#References|[9]]] that the coordinates $ x ^ {i} $ |
| + | can be taken harmonic, i.e. satisfying the equalities $ \sum _ {ij} g ^ {ij} \Gamma _ {ij} ^ {l} = 0 $. | ||
| + | Harmonic coordinate systems form an atlas of class $ C ^ {3, \alpha } $ | ||
| + | for any $ \alpha $, | ||
| + | $ 0 < \alpha < 1 $. | ||
| − | A generalized Riemannian space of bounded curvature with | + | A generalized Riemannian space of bounded curvature with $ K = K ^ \prime $ |
| + | and satisfying conditions 1) and 2) is a Riemannian space of constant [[Riemannian curvature|Riemannian curvature]] $ K $( | ||
| + | see [[#References|[3]]]). | ||
| − | Any Riemannian space of Riemannian curvature contained in between | + | Any Riemannian space of Riemannian curvature contained in between $ K $ |
| + | and $ K ^ \prime $( | ||
| + | $ K ^ \prime \leq K $) | ||
| + | is a generalized Riemannian space of curvature $ \leq K $ | ||
| + | and $ \geq K ^ \prime $ | ||
| + | and satisfies conditions 1) and 2). | ||
A "space of curvature ≤ K" is defined by the left inequality in 2), i.e. by the condition: | A "space of curvature ≤ K" is defined by the left inequality in 2), i.e. by the condition: | ||
| − | + | $ A ^ {-} $) | |
| + | for any sequence of triangles $ T _ {n} $ | ||
| + | contracting to a point, | ||
| − | + | $$ \tag{3 } | |
| + | \overline{\lim\limits}\; | ||
| + | \frac{\overline \delta \; ( T _ {n} ) }{\sigma ( T _ {n} ^ {0} ) } | ||
| + | \leq K. | ||
| + | $$ | ||
| − | Another, equivalent, definition and a starting point for the study of generalized Riemannian spaces are based on the comparison between an arbitrary triangle | + | Another, equivalent, definition and a starting point for the study of generalized Riemannian spaces are based on the comparison between an arbitrary triangle $ T = ABC $ |
| + | and a triangle $ T ^ {k} $ | ||
| + | with sides of the same lengths in a space of constant curvature $ K $. | ||
| + | Let $ \alpha _ {k} , \beta _ {k} , \gamma _ {k} $ | ||
| + | be the angles of such a triangle; the relative upper excess of the triangle $ T $ | ||
| + | is defined as $ \overline \delta \; _ {k} ( T) = ( \widetilde \alpha + \widetilde \beta + \widetilde \gamma ) - ( \alpha _ {k} + \beta _ {k} + \gamma _ {k} ) $. | ||
| + | Condition $ A ^ {-} $) | ||
| + | in the definition of a space of curvature $ \leq K $ | ||
| + | can be replaced by the following condition: | ||
| − | + | $ A _ {1} ^ {-} $) | |
| + | any point has a neighbourhood $ R _ {k} ^ {-} $ | ||
| + | in which $ \overline \delta \; _ {k} ( T) \leq 0 $ | ||
| + | for any triangle $ T $. | ||
| − | An even stronger property of concavity of the metric also holds. Namely, let | + | An even stronger property of concavity of the metric also holds. Namely, let $ L $ |
| + | and $ M $ | ||
| + | be shortests starting at the same point $ O $ | ||
| + | and let $ \gamma _ {k} ( x, y) $ | ||
| + | be the angle in the triangle $ T ^ {k} $ | ||
| + | with sides $ x = \rho ( O, X) $, | ||
| + | $ y = \rho ( O, Y) $, | ||
| + | $ z = \rho ( X, Y) $, | ||
| + | $ X \in L $, | ||
| + | $ Y \in M $, | ||
| + | in a space of constant curvature $ K $, | ||
| + | opposite to the side $ z $. | ||
| + | In $ R _ {k} ^ {-} $( | ||
| + | locally) the angle $ \gamma _ {k} ( x, y) $ | ||
| + | turns out to be a non-decreasing function ( $ \gamma _ {k} ( x _ {1} , y _ {1} ) \leq \gamma _ {k} ( x _ {2} , y _ {2} ) $ | ||
| + | for $ x _ {1} \leq x _ {2} $, | ||
| + | $ y _ {1} \leq y _ {2} $, | ||
| + | a $ k $- | ||
| + | concave metric). Hence one obtains the following local properties: | ||
| − | I) between any two shortests starting at the same point there exists an angle and even an "angle in the strong sense" | + | I) between any two shortests starting at the same point there exists an angle and even an "angle in the strong sense" $ \alpha _ {C} = \lim\limits _ {x,y \rightarrow 0 } \gamma _ {k} ( x, y) $( |
| + | so that, in particular, if $ y = \textrm{ const } $, | ||
| + | $ \lim\limits _ {x\rightarrow} 0 ( y- z)/x = \cos \alpha _ {C} $); | ||
| − | II) for the angles | + | II) for the angles $ \alpha , \beta , \gamma $ |
| + | of a triangle in $ R _ {k} ^ {-} $ | ||
| + | and the corresponding triangle $ T ^ {k} $, | ||
| − | + | $$ | |
| + | \alpha \leq \alpha _ {k} ,\ \beta \leq \beta _ {k} ,\ \gamma \leq \gamma _ {k} ; | ||
| + | $$ | ||
| − | III) in | + | III) in $ R _ {k} ^ {-} $, |
| + | if $ A _ {n} \rightarrow A $, | ||
| + | $ B _ {n} \rightarrow B $, | ||
| + | then the shortests $ A _ {n} B _ {n} \rightarrow AB $( | ||
| + | thus, a shortest with given end points is unique in $ R _ {k} $). | ||
| − | Dual to spaces of curvature | + | Dual to spaces of curvature $ \leq K $ |
| + | are the spaces of curvature $ \geq K $ | ||
| + | subject to the condition dual to $ K $- | ||
| + | concavity: | ||
| − | + | $ A _ {1} ^ {+} $) | |
| + | each point has a neighbourhood $ R _ {k} ^ {+} $ | ||
| + | in which the angle $ \gamma _ {k} ( x, y) $ | ||
| + | for two shortests $ L, M $ | ||
| + | is a non-increasing function (a $ K $- | ||
| + | concave metric, cf. also [[Convex metric|Convex metric]]). | ||
| − | Similarly to spaces of curvature | + | Similarly to spaces of curvature $ \leq K $, |
| + | for spaces of curvature $ \geq K $ | ||
| + | the following (local) properties analogous to I) and II) are valid: Between two shortests there exists an angle in the strong sense; $ \alpha \geq \alpha _ {k} $, | ||
| + | $ \beta \geq \beta _ {k} $, | ||
| + | $ \gamma \geq \gamma _ {k} $ | ||
| + | for any triangle in $ R _ {k} ^ {+} $. | ||
| + | Instead of III) the condition of non-overlapping of shortests or, which is the same, uniqueness of their extension holds: If $ AC \supset AB $ | ||
| + | and $ AC _ {1} \supset AB $ | ||
| + | in $ R _ {k} ^ {+} $, | ||
| + | then either $ AC \supset AC _ {1} $ | ||
| + | or $ AC _ {1} \supset AC $. | ||
| − | Thus, a space of bounded curvature is obtained by combining the conditions determining both classes of spaces — with curvature bounded from above and from below (moreover, on the left-hand side of inequality (3) there is no need to take | + | Thus, a space of bounded curvature is obtained by combining the conditions determining both classes of spaces — with curvature bounded from above and from below (moreover, on the left-hand side of inequality (3) there is no need to take $ \underline \delta $). |
| + | Condition $ A $) | ||
| + | can be replaced, similar to $ A _ {1} ^ {-} $), | ||
| + | by the condition: | ||
| − | + | $ A _ {1} $) | |
| + | each point has a neighbourhood $ R _ {kk ^ \prime } $, | ||
| + | where $ \delta _ {k} ( T) \leq 0 $, | ||
| + | $ \delta _ {k ^ \prime } ( T) \geq 0 $ | ||
| + | for any triangle $ T $. | ||
The above turns out to be equivalent to the following: | The above turns out to be equivalent to the following: | ||
| − | + | $ A _ {2} $) | |
| + | for any quadruple of points in $ R _ {kk ^ \prime } $ | ||
| + | there exists a quadruple of points with the same pairwise distances in a space of constant curvature $ k $, | ||
| + | where $ K ^ \prime \leq k \leq K $ | ||
| + | and $ k $ | ||
| + | depends, in general, on the chosen quadruple of points in $ R _ {kk ^ \prime } $( | ||
| + | see [[#References|[10]]]). | ||
| − | An example of a generalized Riemannian space of curvature | + | An example of a generalized Riemannian space of curvature $ \leq K $ |
| + | $ (\geq K ^ \prime ) $ | ||
| + | is a domain of a Riemannian space such that the Riemannian curvatures of all two-dimensional surface elements at all points of this domain are bounded from above by $ K $( | ||
| + | from below by $ K ^ \prime $). | ||
| − | A set | + | A set $ V $ |
| + | in a space with an internal metric is called convex if any two points $ X, Y \in V $ | ||
| + | can be connected by a shortest $ XY $ | ||
| + | and if every such shortest lies in $ V $. | ||
| − | The following result [[#References|[7]]] has been established: If a space | + | The following result [[#References|[7]]] has been established: If a space $ R $ |
| + | with an internal metric is obtained by glueing together of two spaces $ R ^ \prime , R ^ {\prime\prime} $ | ||
| + | of curvatures $ \leq K $ | ||
| + | along convex sets $ V ^ \prime \subset R ^ \prime $ | ||
| + | and $ V ^ {\prime\prime} \subset R ^ {\prime\prime} $, | ||
| + | then $ R $ | ||
| + | itself is a space of curvature $ \leq K $. | ||
| + | The glueing condition is that $ R = R ^ \prime \cup R ^ {\prime\prime} $, | ||
| + | $ V ^ \prime = V ^ {\prime\prime} = R ^ \prime \cup R ^ {\prime\prime} $ | ||
| + | and the metrics of $ R ^ \prime , R ^ {\prime\prime} $ | ||
| + | are induced by that of the space $ R $. | ||
| − | By definition, two curves | + | By definition, two curves $ L $, |
| + | $ M $ | ||
| + | starting at a point $ O $ | ||
| + | have the same direction at $ O $ | ||
| + | if the upper angle between them is equal to zero (if $ L = M $, | ||
| + | $ L $ | ||
| + | is said to have a definite oriented direction at $ O $). | ||
| + | A direction at the point $ O $ | ||
| + | is defined as a class of curves having the same direction at $ O $. | ||
| + | The directions at the point $ O $ | ||
| + | form a metric space in which the distance between two directions is determined by the upper angle between any two representatives of them. Such a space is called a space of directions at $ O $. | ||
| − | The following has been proved [[#References|[5]]]: If the point | + | The following has been proved [[#References|[5]]]: If the point $ O $ |
| + | lies in a neighbourhood of a space of curvature $ \leq K $ | ||
| + | homeomorphic to $ E ^ {n} $, | ||
| + | then the space of directions at the point $ O $ | ||
| + | has curvature $ \leq 1 $. | ||
| + | In the general case it is not homeomorphic to the $ ( n- 1) $- | ||
| + | dimensional sphere. | ||
| − | In the two-dimensional case, the theory of manifolds of curvature | + | In the two-dimensional case, the theory of manifolds of curvature $ \leq K $ |
| + | is included as a special case in the theory of manifolds of bounded curvature (see [[Two-dimensional manifold of bounded curvature|Two-dimensional manifold of bounded curvature]]). An example of a two-dimensional manifold of curvature $ \leq K $ | ||
| + | is a ruled surface in $ R _ {k} $ | ||
| + | provided with an internal metric, i.e. the surface formed by the interior parts of shortests whose ends cut out two rectifiable curves $ L _ {1} , L _ {2} $. | ||
| + | If the curve $ L _ {2} $ | ||
| + | degenerates to a point $ O $, | ||
| + | the surface is called the cone of shortests spanned from the point $ O $ | ||
| + | over the curve $ L _ {1} $. | ||
| + | If $ L _ {1} $ | ||
| + | is a triangle $ OAB $, | ||
| + | then such a cone is called a surface triangle (see [[#References|[3]]]). | ||
| − | A mapping | + | A mapping $ \phi : M _ {1} \rightarrow M _ {2} $ |
| + | of metric spaces is called non-stretching if $ \rho _ {M _ {1} } ( X, Y) \geq \rho _ {M _ {2} } ( \phi ( X), \phi ( Y)) $ | ||
| + | for any $ X, Y \in M _ {1} $. | ||
| + | A mapping $ \phi : \Gamma _ {1} \rightarrow \Gamma _ {2} $ | ||
| + | of a closed curve $ \Gamma _ {1} $ | ||
| + | in $ M _ {1} $ | ||
| + | onto a closed curve $ \Gamma _ {2} $ | ||
| + | in $ M _ {2} $ | ||
| + | is called length-preserving if the lengths of corresponding arcs of $ \Gamma _ {1} $ | ||
| + | and $ \Gamma _ {2} $ | ||
| + | coincide under $ \phi $. | ||
| + | Let $ V $ | ||
| + | be a convex domain in a space of constant curvature $ K $ | ||
| + | and $ L $ | ||
| + | be the boundary contour of $ V $. | ||
| + | The domain $ V $ | ||
| + | is said to majorize a closed curve $ \Gamma $ | ||
| + | in a metric space $ M $ | ||
| + | if there exists a non-stretching mapping from $ V $ | ||
| + | into $ M $ | ||
| + | that is length-preserving from $ L $ | ||
| + | to $ \Gamma $. | ||
| + | The mapping itself is called majorizing. | ||
| − | Let | + | Let $ R _ {k} $ |
| + | be a convex space with an internal metric; let $ C $ | ||
| + | be the cone of shortests spanned over a closed rectifiable curve $ \Gamma $ | ||
| + | in $ R _ {k} $ | ||
| + | from a point $ O \in \Gamma $, | ||
| + | and, moreover, let, if $ K > 0 $, | ||
| + | the length $ l $ | ||
| + | of $ \Gamma $ | ||
| + | be less than $ 2 \pi / \sqrt K $. | ||
| + | Then in a space of constant curvature $ K $ | ||
| + | there exists a convex domain $ V $ | ||
| + | majorizing $ \Gamma $ | ||
| + | and such that $ \phi ( V) = C $ | ||
| + | for the corresponding majorizing mapping $ \phi $. | ||
| + | This property is characteristic for spaces of curvature $ \leq K $. | ||
| + | The existence of a length-preserving non-stretching mapping of the contour $ L $ | ||
| + | of $ V $ | ||
| + | onto $ \Gamma $ | ||
| + | is already sufficient (see [[#References|[8]]]). | ||
| − | A continuous mapping | + | A continuous mapping $ f $ |
| + | from a disc $ B $ | ||
| + | into a metric space $ M $ | ||
| + | is called a surface in $ M $. | ||
| + | Let $ P $ | ||
| + | be a triangulated polygon, i.e. a complex of triangles $ T _ {i} $ | ||
| + | inscribed in $ B $. | ||
| + | To the triangle $ T _ {i} $ | ||
| + | with vertices $ X, Y, Z $ | ||
| + | there corresponds the Euclidean triangle $ T _ {i} ^ {0} $ | ||
| + | with sides equal to the distances between points $ f( X), f( Y), f( Z) $. | ||
| + | Let $ S _ {0} ( P) $ | ||
| + | be the sum of the areas $ S( T _ {i} ^ {0} ) $ | ||
| + | of all triangles $ T _ {i} ^ {0} $; | ||
| + | then the area $ S( f ) $ | ||
| + | of the surface $ f $ | ||
| + | is defined (see [[#References|[3]]]) as the [[limes inferior]] of $ S _ {0} ( f ) $ | ||
| + | under the condition that the vertices of $ P $ | ||
| + | unboundedly contract in $ B $: | ||
| + | $ S( f ) = \lim\limits S _ {0} ( P) $. | ||
| + | This definition is modified as follows (see [[#References|[6]]]). Instead of $ f( X), f( Y), f( Z) $, | ||
| + | the vertices $ X, Y, Z $ | ||
| + | of the triangle $ T _ {i} $ | ||
| + | of the complex $ P $ | ||
| + | are put into correspondence with points $ X ^ {P} , Y ^ {P} , Z ^ {P} $ | ||
| + | in $ M $, | ||
| + | where, moreover, to vertices of the complex $ P $ | ||
| + | correspond the same points if and only if the images of the vertices under $ f $ | ||
| + | coincide. For the area $ L( f ) $ | ||
| + | of the surface $ f $ | ||
| + | one takes the limes inferior of the sums of the areas of the Euclidean triangles $ T _ {i} ^ {0} $ | ||
| + | with sides equal to the distances between $ X ^ {P} , Y ^ {P} , Z ^ {P} $, | ||
| + | under the additional assumption that $ \rho ( f( X _ {k} ), X _ {k} ^ {P} ) $ | ||
| + | tends to zero for all vertices $ X _ {k} $ | ||
| + | of the complex $ P $. | ||
| + | One always has $ L( f ) \leq S( f ) $. | ||
| − | + | $ \alpha $) | |
| + | If a sequence of surfaces $ f _ {n} $ | ||
| + | in $ R _ {k} $ | ||
| + | converges uniformly to a surface $ f $, | ||
| + | then | ||
| − | + | $$ | |
| + | L( f ) \leq \lim\limits L( f _ {n} ) \ ( \textrm{ semi"\AAh"continuity } ). | ||
| + | $$ | ||
| − | + | $ \beta $) | |
| + | If $ p $ | ||
| + | is a non-stretching mapping from $ R _ {k} $ | ||
| + | into $ R _ {k} $ | ||
| + | and $ f $ | ||
| + | is a surface in $ R _ {k} $, | ||
| + | then | ||
| − | + | $$ | |
| + | L( p \circ f ) \leq L( f ) \ ( \textrm{ Kolmogorov\prime s principle } ). | ||
| + | $$ | ||
| − | + | $ \delta $) | |
| + | The area $ S( f ) $ | ||
| + | of a surface triangle $ T $ | ||
| + | in $ R _ {k} $ | ||
| + | is not larger than the area of the corresponding triangle $ T ^ {k} $ | ||
| + | and is equal to it if and only if $ T $ | ||
| + | is isometric to $ T ^ {k} $( | ||
| + | the local property). | ||
| − | + | $ \gamma $) | |
| + | Under the conditions of the existence theorem for a majorizing mapping (see above), the area $ S( G) $ | ||
| + | is not larger than the area of the disc of perimeter 1 in a space of constant curvature $ K $( | ||
| + | the isoperimetric inequality) (see [[#References|[3]]], [[#References|[6]]]). | ||
| − | In [[#References|[6]]] the [[Plateau problem|Plateau problem]] on the existence of a surface of minimal area spanned over a closed curve | + | In [[#References|[6]]] the [[Plateau problem|Plateau problem]] on the existence of a surface of minimal area spanned over a closed curve $ \Gamma $ |
| + | in $ R _ {k} $ | ||
| + | is solved. The following has been proved. Let $ R _ {k} $ | ||
| + | be a metrically-complete space of curvature $ \leq K $( | ||
| + | for $ K > 0 $, | ||
| + | the diameter $ d( R _ {k} ) < \pi /2 \sqrt K $) | ||
| + | and let $ \Gamma $ | ||
| + | be a closed Jordan curve in $ R _ {k} $. | ||
| + | Then there exists a surface $ f $ | ||
| + | of minimal area $ L( f ) $ | ||
| + | spanned over the curve $ \Gamma $. | ||
| + | Let $ \Gamma , \Gamma _ {n} $, | ||
| + | $ n = 1, 2 \dots $ | ||
| + | be closed Jordan curves in such a space and let $ a( \Gamma ) $, | ||
| + | $ a( \Gamma _ {n} ) $ | ||
| + | be the minimal areas of the surfaces spanned over $ \Gamma $ | ||
| + | and $ \Gamma _ {n} $, | ||
| + | respectively. If the $ \Gamma _ {n} $ | ||
| + | converge under some parametrizations uniformly to $ \Gamma $, | ||
| + | then $ a( \Gamma ) \geq \lim\limits a( \Gamma _ {n} ) $. | ||
Two-dimensional manifolds with an indefinite metric of bounded curvature have been studied. The problem of a coordinate-free definition of multi-dimensional spaces with an indefinite metric of bounded curvature, and, in particular, of spaces in the general theory of relativity, has not yet been solved (1990). | Two-dimensional manifolds with an indefinite metric of bounded curvature have been studied. The problem of a coordinate-free definition of multi-dimensional spaces with an indefinite metric of bounded curvature, and, in particular, of spaces in the general theory of relativity, has not yet been solved (1990). | ||
| Line 95: | Line 399: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.D. Aleksandrov, "Die innere Geometrie der konvexen Flächen" , Akademie Verlag (1955) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.D. Aleksandrov, "A theorem on triangles in metric space and certain applications" ''Trudy Mat. Inst. Steklov.'' , '''38''' (1951) pp. 5–23 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.D. [A.D. Aleksandrov ] Alexandroff, "Über eine Verallgemeinerung der Riemannschen Geometrie" ''Schrift. Inst. Math. Deutsch. Akad. Wiss.'' , '''1''' (1957) pp. 33–84</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.N. Berestovskii, "Introduction of a Riemann structure into certain metric spaces" ''Sib. Math. J.'' , '''16''' : 4 (1975) pp. 499–507 ''Sibirsk. Mat. Zh.'' , '''16''' : 4 (1975) pp. 651–662</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> I.G. Nikolaev, "Space of directions at a point in a space of curvature not greater than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082200/r082200296.png" />" ''Sib. Math. J.'' , '''19''' : 6 (1978) pp. 944–948 ''Sibirsk. Math. Zh.'' , '''19''' : 6 (1978) pp. 1341–1348</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> I.G. Nikolaev, "Solution of Plateau's problem in spaces of curvature not greater than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082200/r082200297.png" />" ''Sib. Math. J.'' , '''20''' : 2 (1979) pp. 246–251 ''Sibirsk. Mat. Zh.'' , '''20''' : 2 (1979) pp. 345–353</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> Yu.G. Reshetnyak, "To the theory of spaces with curvature not greater than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082200/r082200298.png" />" ''Mat. Sb.'' , '''52''' : 3 (1960) pp. 789–798 (In Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> Yu.G. Reshetnyak, "Inextensible mappings in a space of curvature no greater than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082200/r082200299.png" />" ''Sib. Math. J.'' , '''9''' : 4 (1968) pp. 683–689 ''Sibirsk. Mat. Zh.'' , '''9''' : 4 (1968) pp. 918–927</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> I.G. Nikolaev, "Smoothness of the metric of spaces with two-sided bounded A.D. Aleksandrov curvature" ''Sib. Math. J.'' , '''24''' : 2 (1983) pp. 247–263 ''Sibersk. Mat. Zh.'' , '''24''' : 2 (1983) pp. 114–132</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> V.N. Berestovskii, "Spaces with bounded curvature and distance geometry" ''Sib. Math. J.'' , '''27''' : 1 (1986) pp. 8–18 ''Sibersk. Mat. Zh.'' , '''27''' : 1 (1986) pp. 11–25</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.D. Aleksandrov, "Die innere Geometrie der konvexen Flächen" , Akademie Verlag (1955) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.D. Aleksandrov, "A theorem on triangles in metric space and certain applications" ''Trudy Mat. Inst. Steklov.'' , '''38''' (1951) pp. 5–23 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.D. [A.D. Aleksandrov ] Alexandroff, "Über eine Verallgemeinerung der Riemannschen Geometrie" ''Schrift. Inst. Math. Deutsch. Akad. Wiss.'' , '''1''' (1957) pp. 33–84</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.N. Berestovskii, "Introduction of a Riemann structure into certain metric spaces" ''Sib. Math. J.'' , '''16''' : 4 (1975) pp. 499–507 ''Sibirsk. Mat. Zh.'' , '''16''' : 4 (1975) pp. 651–662</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> I.G. Nikolaev, "Space of directions at a point in a space of curvature not greater than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082200/r082200296.png" />" ''Sib. Math. J.'' , '''19''' : 6 (1978) pp. 944–948 ''Sibirsk. Math. Zh.'' , '''19''' : 6 (1978) pp. 1341–1348</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> I.G. Nikolaev, "Solution of Plateau's problem in spaces of curvature not greater than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082200/r082200297.png" />" ''Sib. Math. J.'' , '''20''' : 2 (1979) pp. 246–251 ''Sibirsk. Mat. Zh.'' , '''20''' : 2 (1979) pp. 345–353</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> Yu.G. Reshetnyak, "To the theory of spaces with curvature not greater than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082200/r082200298.png" />" ''Mat. Sb.'' , '''52''' : 3 (1960) pp. 789–798 (In Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> Yu.G. Reshetnyak, "Inextensible mappings in a space of curvature no greater than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082200/r082200299.png" />" ''Sib. Math. J.'' , '''9''' : 4 (1968) pp. 683–689 ''Sibirsk. Mat. Zh.'' , '''9''' : 4 (1968) pp. 918–927</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> I.G. Nikolaev, "Smoothness of the metric of spaces with two-sided bounded A.D. Aleksandrov curvature" ''Sib. Math. J.'' , '''24''' : 2 (1983) pp. 247–263 ''Sibersk. Mat. Zh.'' , '''24''' : 2 (1983) pp. 114–132</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> V.N. Berestovskii, "Spaces with bounded curvature and distance geometry" ''Sib. Math. J.'' , '''27''' : 1 (1986) pp. 8–18 ''Sibersk. Mat. Zh.'' , '''27''' : 1 (1986) pp. 11–25</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Rinow, "Die innere Geometrie der metrischen Räume" , Springer (1961)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Gromov, "Structures métriques pour les variétés riemanniennes" , Cedec-Nathan (1981) (Translated from Russian)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> "Elie Cartan et les mathématiques d'aujourd'hui" ''Astérisque'' (1985)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A.V. Pogorelov, "Intrinsic geometry of surfaces" , Amer. Math. Soc. (1973) (Translated from Russian)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H. Busemann, "The geometry of geodesics" , Acad. Press (1955)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Rinow, "Die innere Geometrie der metrischen Räume" , Springer (1961)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Gromov, "Structures métriques pour les variétés riemanniennes" , Cedec-Nathan (1981) (Translated from Russian)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> "Elie Cartan et les mathématiques d'aujourd'hui" ''Astérisque'' (1985)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A.V. Pogorelov, "Intrinsic geometry of surfaces" , Amer. Math. Soc. (1973) (Translated from Russian)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H. Busemann, "The geometry of geodesics" , Acad. Press (1955)</TD></TR></table> | ||
Latest revision as of 08:11, 6 June 2020
A space with an internal metric subject to certain restrictions on the curvature. Spaces of "bounded curvature from above" and others belong to this class (see [3]). Generalized Riemannian spaces differ from Riemannian spaces (cf. Riemannian space) not only by greater generality but also by the fact that they are defined and studied on the basis of their metric alone, without coordinates. Under a certain combination of conditions concerning the curvature and the behaviour of shortests curves (i.e. curves whose lengths are equal to the distances between the end points), a generalized Riemannian space turns out to be Riemannian, which gives a purely metric definition of a Riemannian space.
Definitions of generalized Riemannian spaces are based on the classical relation between the curvature and the excess of a geodesic triangle (excess $ = $ sum of the angles minus $ \pi $). These concepts are carried over to a space with an internal metric, such that each point of it has a neighbourhood in which any two points can be connected by a shortest curve. This condition is assumed hereafter without further stipulation. A triangle $ T = ABC $ is triplet of shortests curves $ AB, BC, CA $— the sides of the triangle — connecting in pairs three different points $ A, B, C $— the vertices of the triangle. The angle between curves can be defined in any metric space: Let $ L, M $ be curves starting at the same point $ O $ in a space with metric $ \rho $. One chooses points $ X \in L $, $ Y \in M $ $ ( X, Y \neq O) $ and constructs the Euclidean triangle with sides $ x = \rho ( O, X) $, $ y = \rho ( O, Y) $, $ z = \rho ( X, Y) $ and angle $ \gamma ( x, y) $ opposite to the side $ z $. One defines the upper angle between $ L $ and $ M $ as:
$$ \tag{1 } \overline \alpha \; = \overline{\lim\limits}\; _ {x,y \rightarrow 0 } \gamma ( x, y). $$
The upper angles of the triangle are the upper angles $ \widetilde \alpha , \widetilde \beta , \widetilde \gamma $ between its sides at the vertices $ A, B, C $ and the excess of the triangle is $ \overline \delta \; ( T) = \widetilde \alpha + \widetilde \beta + \widetilde \gamma - \pi $.
A generalized Riemannian space of bounded curvature ( $ \leq K $ and $ \geq K ^ \prime $) is defined by the following condition:
$ A $) for any sequence of triangles $ T _ {n} $ contracting to a point,
$$ \tag{2 } K \geq \overline{\lim\limits}\; \frac{\overline \delta \; ( T _ {n} ) }{\sigma ( T _ {n} ^ {0} ) } \geq fnnme \underline{lim} \frac{\overline \delta \; ( T _ {n} ) }{\sigma ( T _ {n} ^ {0} ) } \geq K ^ \prime , $$
where $ \sigma ( T _ {n} ^ {0} ) $ is the area of the Euclidean triangle with the same sides as $ T _ {n} $( if $ \sigma ( T _ {n} ^ {0} ) = 0 $, then $ \overline \delta \; ( T _ {n} ) = 0 $). Such a space turns out to be Riemannian under two natural additional conditions:
1) local compactness of the space (in a space with an internal metric this already ensures the condition of local existence of shortests);
2) local extendibility of shortests, i.e. each point has a neighbourhood $ U $ such that any shortest $ XY $, where $ X, Y \in U $, can be extended beyond its end points. Under all these conditions the space is Riemannian (see [4]); moreover, in a neighbourhood of each point one can introduce coordinates $ x ^ {i} $ so that the metric will be given by a line element $ ds ^ {2} = g _ {ij} dx ^ {i} dx ^ {j} $ with coefficients $ g _ {ij} \in W _ {q} ^ {2} \cap C ^ {1, \alpha } $, $ 0 < \alpha < 1 $. Thus, a parallel displacement is given (with continuous $ \Gamma _ {jk} ^ {i} $) and, almost everywhere, a curvature tensor (see [9]).
Moreover, it has been proved [9] that the coordinates $ x ^ {i} $ can be taken harmonic, i.e. satisfying the equalities $ \sum _ {ij} g ^ {ij} \Gamma _ {ij} ^ {l} = 0 $. Harmonic coordinate systems form an atlas of class $ C ^ {3, \alpha } $ for any $ \alpha $, $ 0 < \alpha < 1 $.
A generalized Riemannian space of bounded curvature with $ K = K ^ \prime $ and satisfying conditions 1) and 2) is a Riemannian space of constant Riemannian curvature $ K $( see [3]).
Any Riemannian space of Riemannian curvature contained in between $ K $ and $ K ^ \prime $( $ K ^ \prime \leq K $) is a generalized Riemannian space of curvature $ \leq K $ and $ \geq K ^ \prime $ and satisfies conditions 1) and 2).
A "space of curvature ≤ K" is defined by the left inequality in 2), i.e. by the condition:
$ A ^ {-} $) for any sequence of triangles $ T _ {n} $ contracting to a point,
$$ \tag{3 } \overline{\lim\limits}\; \frac{\overline \delta \; ( T _ {n} ) }{\sigma ( T _ {n} ^ {0} ) } \leq K. $$
Another, equivalent, definition and a starting point for the study of generalized Riemannian spaces are based on the comparison between an arbitrary triangle $ T = ABC $ and a triangle $ T ^ {k} $ with sides of the same lengths in a space of constant curvature $ K $. Let $ \alpha _ {k} , \beta _ {k} , \gamma _ {k} $ be the angles of such a triangle; the relative upper excess of the triangle $ T $ is defined as $ \overline \delta \; _ {k} ( T) = ( \widetilde \alpha + \widetilde \beta + \widetilde \gamma ) - ( \alpha _ {k} + \beta _ {k} + \gamma _ {k} ) $. Condition $ A ^ {-} $) in the definition of a space of curvature $ \leq K $ can be replaced by the following condition:
$ A _ {1} ^ {-} $) any point has a neighbourhood $ R _ {k} ^ {-} $ in which $ \overline \delta \; _ {k} ( T) \leq 0 $ for any triangle $ T $.
An even stronger property of concavity of the metric also holds. Namely, let $ L $ and $ M $ be shortests starting at the same point $ O $ and let $ \gamma _ {k} ( x, y) $ be the angle in the triangle $ T ^ {k} $ with sides $ x = \rho ( O, X) $, $ y = \rho ( O, Y) $, $ z = \rho ( X, Y) $, $ X \in L $, $ Y \in M $, in a space of constant curvature $ K $, opposite to the side $ z $. In $ R _ {k} ^ {-} $( locally) the angle $ \gamma _ {k} ( x, y) $ turns out to be a non-decreasing function ( $ \gamma _ {k} ( x _ {1} , y _ {1} ) \leq \gamma _ {k} ( x _ {2} , y _ {2} ) $ for $ x _ {1} \leq x _ {2} $, $ y _ {1} \leq y _ {2} $, a $ k $- concave metric). Hence one obtains the following local properties:
I) between any two shortests starting at the same point there exists an angle and even an "angle in the strong sense" $ \alpha _ {C} = \lim\limits _ {x,y \rightarrow 0 } \gamma _ {k} ( x, y) $( so that, in particular, if $ y = \textrm{ const } $, $ \lim\limits _ {x\rightarrow} 0 ( y- z)/x = \cos \alpha _ {C} $);
II) for the angles $ \alpha , \beta , \gamma $ of a triangle in $ R _ {k} ^ {-} $ and the corresponding triangle $ T ^ {k} $,
$$ \alpha \leq \alpha _ {k} ,\ \beta \leq \beta _ {k} ,\ \gamma \leq \gamma _ {k} ; $$
III) in $ R _ {k} ^ {-} $, if $ A _ {n} \rightarrow A $, $ B _ {n} \rightarrow B $, then the shortests $ A _ {n} B _ {n} \rightarrow AB $( thus, a shortest with given end points is unique in $ R _ {k} $).
Dual to spaces of curvature $ \leq K $ are the spaces of curvature $ \geq K $ subject to the condition dual to $ K $- concavity:
$ A _ {1} ^ {+} $) each point has a neighbourhood $ R _ {k} ^ {+} $ in which the angle $ \gamma _ {k} ( x, y) $ for two shortests $ L, M $ is a non-increasing function (a $ K $- concave metric, cf. also Convex metric).
Similarly to spaces of curvature $ \leq K $, for spaces of curvature $ \geq K $ the following (local) properties analogous to I) and II) are valid: Between two shortests there exists an angle in the strong sense; $ \alpha \geq \alpha _ {k} $, $ \beta \geq \beta _ {k} $, $ \gamma \geq \gamma _ {k} $ for any triangle in $ R _ {k} ^ {+} $. Instead of III) the condition of non-overlapping of shortests or, which is the same, uniqueness of their extension holds: If $ AC \supset AB $ and $ AC _ {1} \supset AB $ in $ R _ {k} ^ {+} $, then either $ AC \supset AC _ {1} $ or $ AC _ {1} \supset AC $.
Thus, a space of bounded curvature is obtained by combining the conditions determining both classes of spaces — with curvature bounded from above and from below (moreover, on the left-hand side of inequality (3) there is no need to take $ \underline \delta $). Condition $ A $) can be replaced, similar to $ A _ {1} ^ {-} $), by the condition:
$ A _ {1} $) each point has a neighbourhood $ R _ {kk ^ \prime } $, where $ \delta _ {k} ( T) \leq 0 $, $ \delta _ {k ^ \prime } ( T) \geq 0 $ for any triangle $ T $.
The above turns out to be equivalent to the following:
$ A _ {2} $) for any quadruple of points in $ R _ {kk ^ \prime } $ there exists a quadruple of points with the same pairwise distances in a space of constant curvature $ k $, where $ K ^ \prime \leq k \leq K $ and $ k $ depends, in general, on the chosen quadruple of points in $ R _ {kk ^ \prime } $( see [10]).
An example of a generalized Riemannian space of curvature $ \leq K $ $ (\geq K ^ \prime ) $ is a domain of a Riemannian space such that the Riemannian curvatures of all two-dimensional surface elements at all points of this domain are bounded from above by $ K $( from below by $ K ^ \prime $).
A set $ V $ in a space with an internal metric is called convex if any two points $ X, Y \in V $ can be connected by a shortest $ XY $ and if every such shortest lies in $ V $.
The following result [7] has been established: If a space $ R $ with an internal metric is obtained by glueing together of two spaces $ R ^ \prime , R ^ {\prime\prime} $ of curvatures $ \leq K $ along convex sets $ V ^ \prime \subset R ^ \prime $ and $ V ^ {\prime\prime} \subset R ^ {\prime\prime} $, then $ R $ itself is a space of curvature $ \leq K $. The glueing condition is that $ R = R ^ \prime \cup R ^ {\prime\prime} $, $ V ^ \prime = V ^ {\prime\prime} = R ^ \prime \cup R ^ {\prime\prime} $ and the metrics of $ R ^ \prime , R ^ {\prime\prime} $ are induced by that of the space $ R $.
By definition, two curves $ L $, $ M $ starting at a point $ O $ have the same direction at $ O $ if the upper angle between them is equal to zero (if $ L = M $, $ L $ is said to have a definite oriented direction at $ O $). A direction at the point $ O $ is defined as a class of curves having the same direction at $ O $. The directions at the point $ O $ form a metric space in which the distance between two directions is determined by the upper angle between any two representatives of them. Such a space is called a space of directions at $ O $.
The following has been proved [5]: If the point $ O $ lies in a neighbourhood of a space of curvature $ \leq K $ homeomorphic to $ E ^ {n} $, then the space of directions at the point $ O $ has curvature $ \leq 1 $. In the general case it is not homeomorphic to the $ ( n- 1) $- dimensional sphere.
In the two-dimensional case, the theory of manifolds of curvature $ \leq K $ is included as a special case in the theory of manifolds of bounded curvature (see Two-dimensional manifold of bounded curvature). An example of a two-dimensional manifold of curvature $ \leq K $ is a ruled surface in $ R _ {k} $ provided with an internal metric, i.e. the surface formed by the interior parts of shortests whose ends cut out two rectifiable curves $ L _ {1} , L _ {2} $. If the curve $ L _ {2} $ degenerates to a point $ O $, the surface is called the cone of shortests spanned from the point $ O $ over the curve $ L _ {1} $. If $ L _ {1} $ is a triangle $ OAB $, then such a cone is called a surface triangle (see [3]).
A mapping $ \phi : M _ {1} \rightarrow M _ {2} $ of metric spaces is called non-stretching if $ \rho _ {M _ {1} } ( X, Y) \geq \rho _ {M _ {2} } ( \phi ( X), \phi ( Y)) $ for any $ X, Y \in M _ {1} $. A mapping $ \phi : \Gamma _ {1} \rightarrow \Gamma _ {2} $ of a closed curve $ \Gamma _ {1} $ in $ M _ {1} $ onto a closed curve $ \Gamma _ {2} $ in $ M _ {2} $ is called length-preserving if the lengths of corresponding arcs of $ \Gamma _ {1} $ and $ \Gamma _ {2} $ coincide under $ \phi $. Let $ V $ be a convex domain in a space of constant curvature $ K $ and $ L $ be the boundary contour of $ V $. The domain $ V $ is said to majorize a closed curve $ \Gamma $ in a metric space $ M $ if there exists a non-stretching mapping from $ V $ into $ M $ that is length-preserving from $ L $ to $ \Gamma $. The mapping itself is called majorizing.
Let $ R _ {k} $ be a convex space with an internal metric; let $ C $ be the cone of shortests spanned over a closed rectifiable curve $ \Gamma $ in $ R _ {k} $ from a point $ O \in \Gamma $, and, moreover, let, if $ K > 0 $, the length $ l $ of $ \Gamma $ be less than $ 2 \pi / \sqrt K $. Then in a space of constant curvature $ K $ there exists a convex domain $ V $ majorizing $ \Gamma $ and such that $ \phi ( V) = C $ for the corresponding majorizing mapping $ \phi $. This property is characteristic for spaces of curvature $ \leq K $. The existence of a length-preserving non-stretching mapping of the contour $ L $ of $ V $ onto $ \Gamma $ is already sufficient (see [8]).
A continuous mapping $ f $ from a disc $ B $ into a metric space $ M $ is called a surface in $ M $. Let $ P $ be a triangulated polygon, i.e. a complex of triangles $ T _ {i} $ inscribed in $ B $. To the triangle $ T _ {i} $ with vertices $ X, Y, Z $ there corresponds the Euclidean triangle $ T _ {i} ^ {0} $ with sides equal to the distances between points $ f( X), f( Y), f( Z) $. Let $ S _ {0} ( P) $ be the sum of the areas $ S( T _ {i} ^ {0} ) $ of all triangles $ T _ {i} ^ {0} $; then the area $ S( f ) $ of the surface $ f $ is defined (see [3]) as the limes inferior of $ S _ {0} ( f ) $ under the condition that the vertices of $ P $ unboundedly contract in $ B $: $ S( f ) = \lim\limits S _ {0} ( P) $. This definition is modified as follows (see [6]). Instead of $ f( X), f( Y), f( Z) $, the vertices $ X, Y, Z $ of the triangle $ T _ {i} $ of the complex $ P $ are put into correspondence with points $ X ^ {P} , Y ^ {P} , Z ^ {P} $ in $ M $, where, moreover, to vertices of the complex $ P $ correspond the same points if and only if the images of the vertices under $ f $ coincide. For the area $ L( f ) $ of the surface $ f $ one takes the limes inferior of the sums of the areas of the Euclidean triangles $ T _ {i} ^ {0} $ with sides equal to the distances between $ X ^ {P} , Y ^ {P} , Z ^ {P} $, under the additional assumption that $ \rho ( f( X _ {k} ), X _ {k} ^ {P} ) $ tends to zero for all vertices $ X _ {k} $ of the complex $ P $. One always has $ L( f ) \leq S( f ) $.
$ \alpha $) If a sequence of surfaces $ f _ {n} $ in $ R _ {k} $ converges uniformly to a surface $ f $, then
$$ L( f ) \leq \lim\limits L( f _ {n} ) \ ( \textrm{ semi"\AAh"continuity } ). $$
$ \beta $) If $ p $ is a non-stretching mapping from $ R _ {k} $ into $ R _ {k} $ and $ f $ is a surface in $ R _ {k} $, then
$$ L( p \circ f ) \leq L( f ) \ ( \textrm{ Kolmogorov\prime s principle } ). $$
$ \delta $) The area $ S( f ) $ of a surface triangle $ T $ in $ R _ {k} $ is not larger than the area of the corresponding triangle $ T ^ {k} $ and is equal to it if and only if $ T $ is isometric to $ T ^ {k} $( the local property).
$ \gamma $) Under the conditions of the existence theorem for a majorizing mapping (see above), the area $ S( G) $ is not larger than the area of the disc of perimeter 1 in a space of constant curvature $ K $( the isoperimetric inequality) (see [3], [6]).
In [6] the Plateau problem on the existence of a surface of minimal area spanned over a closed curve $ \Gamma $ in $ R _ {k} $ is solved. The following has been proved. Let $ R _ {k} $ be a metrically-complete space of curvature $ \leq K $( for $ K > 0 $, the diameter $ d( R _ {k} ) < \pi /2 \sqrt K $) and let $ \Gamma $ be a closed Jordan curve in $ R _ {k} $. Then there exists a surface $ f $ of minimal area $ L( f ) $ spanned over the curve $ \Gamma $. Let $ \Gamma , \Gamma _ {n} $, $ n = 1, 2 \dots $ be closed Jordan curves in such a space and let $ a( \Gamma ) $, $ a( \Gamma _ {n} ) $ be the minimal areas of the surfaces spanned over $ \Gamma $ and $ \Gamma _ {n} $, respectively. If the $ \Gamma _ {n} $ converge under some parametrizations uniformly to $ \Gamma $, then $ a( \Gamma ) \geq \lim\limits a( \Gamma _ {n} ) $.
Two-dimensional manifolds with an indefinite metric of bounded curvature have been studied. The problem of a coordinate-free definition of multi-dimensional spaces with an indefinite metric of bounded curvature, and, in particular, of spaces in the general theory of relativity, has not yet been solved (1990).
References
| [1] | A.D. Aleksandrov, "Die innere Geometrie der konvexen Flächen" , Akademie Verlag (1955) (Translated from Russian) |
| [2] | A.D. Aleksandrov, "A theorem on triangles in metric space and certain applications" Trudy Mat. Inst. Steklov. , 38 (1951) pp. 5–23 (In Russian) |
| [3] | A.D. [A.D. Aleksandrov ] Alexandroff, "Über eine Verallgemeinerung der Riemannschen Geometrie" Schrift. Inst. Math. Deutsch. Akad. Wiss. , 1 (1957) pp. 33–84 |
| [4] | V.N. Berestovskii, "Introduction of a Riemann structure into certain metric spaces" Sib. Math. J. , 16 : 4 (1975) pp. 499–507 Sibirsk. Mat. Zh. , 16 : 4 (1975) pp. 651–662 |
| [5] | I.G. Nikolaev, "Space of directions at a point in a space of curvature not greater than  " Sib. Math. J. , 19 : 6 (1978) pp. 944–948 Sibirsk. Math. Zh. , 19 : 6 (1978) pp. 1341–1348 " Sib. Math. J. , 19 : 6 (1978) pp. 944–948 Sibirsk. Math. Zh. , 19 : 6 (1978) pp. 1341–1348 |
| [6] | I.G. Nikolaev, "Solution of Plateau's problem in spaces of curvature not greater than 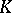 " Sib. Math. J. , 20 : 2 (1979) pp. 246–251 Sibirsk. Mat. Zh. , 20 : 2 (1979) pp. 345–353 " Sib. Math. J. , 20 : 2 (1979) pp. 246–251 Sibirsk. Mat. Zh. , 20 : 2 (1979) pp. 345–353 |
| [7] | Yu.G. Reshetnyak, "To the theory of spaces with curvature not greater than 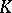 " Mat. Sb. , 52 : 3 (1960) pp. 789–798 (In Russian) " Mat. Sb. , 52 : 3 (1960) pp. 789–798 (In Russian) |
| [8] | Yu.G. Reshetnyak, "Inextensible mappings in a space of curvature no greater than 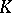 " Sib. Math. J. , 9 : 4 (1968) pp. 683–689 Sibirsk. Mat. Zh. , 9 : 4 (1968) pp. 918–927 " Sib. Math. J. , 9 : 4 (1968) pp. 683–689 Sibirsk. Mat. Zh. , 9 : 4 (1968) pp. 918–927 |
| [9] | I.G. Nikolaev, "Smoothness of the metric of spaces with two-sided bounded A.D. Aleksandrov curvature" Sib. Math. J. , 24 : 2 (1983) pp. 247–263 Sibersk. Mat. Zh. , 24 : 2 (1983) pp. 114–132 |
| [10] | V.N. Berestovskii, "Spaces with bounded curvature and distance geometry" Sib. Math. J. , 27 : 1 (1986) pp. 8–18 Sibersk. Mat. Zh. , 27 : 1 (1986) pp. 11–25 |
Comments
References
| [a1] | W. Rinow, "Die innere Geometrie der metrischen Räume" , Springer (1961) |
| [a2] | M. Gromov, "Structures métriques pour les variétés riemanniennes" , Cedec-Nathan (1981) (Translated from Russian) |
| [a3] | "Elie Cartan et les mathématiques d'aujourd'hui" Astérisque (1985) |
| [a4] | A.V. Pogorelov, "Intrinsic geometry of surfaces" , Amer. Math. Soc. (1973) (Translated from Russian) |
| [a5] | H. Busemann, "The geometry of geodesics" , Acad. Press (1955) |
Riemannian space, generalized. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemannian_space,_generalized&oldid=19196