Difference between revisions of "Representation of a partially ordered set"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | r0814001.png | ||
| + | $#A+1 = 30 n = 0 | ||
| + | $#C+1 = 30 : ~/encyclopedia/old_files/data/R081/R.0801400 Representation of a partially ordered set | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| + | |||
| + | Let $ S $ | ||
| + | be a [[Partially ordered set|partially ordered set]] and $ k $ | ||
| + | a [[Field|field]]. Let $ \omega $ | ||
| + | be a symbol with $ \omega \notin S $. | ||
| + | An $ S $- | ||
| + | space is of the form $ V=( V _ \omega , V _ {s} ) _ {s \in S } $, | ||
| + | where the $ V _ {s} $ | ||
| + | are subspaces of the $ k $- | ||
| + | space $ V _ \omega $ | ||
| + | for $ s \in S $, | ||
| + | such that $ s \leq s ^ \prime $ | ||
| + | implies $ V _ {s} \subset V _ {s ^ \prime } $. | ||
| + | Let $ V , V ^ \prime $ | ||
| + | be $ S $- | ||
| + | spaces; a mapping $ f: V \rightarrow V ^ \prime $ | ||
| + | is a $ k $- | ||
| + | linear mapping $ V _ \omega \rightarrow V _ \omega ^ \prime $ | ||
| + | such that $ f( V _ {s} ) \subset V _ {s} ^ \prime $ | ||
| + | for all $ s \in S $. | ||
| + | The direct sum of $ V $ | ||
| + | and $ V ^ \prime $ | ||
| + | is $ V \oplus V ^ \prime $ | ||
| + | with $ ( V \oplus V ^ \prime ) _ {s} = V _ {s} \oplus V _ {s} ^ \prime $ | ||
| + | for all $ s \in S \cup \{ \omega \} $. | ||
| + | An $ S $- | ||
| + | space is said to be indecomposable if it cannot be written as the direct sum of two non-zero $ S $- | ||
| + | spaces. | ||
| + | |||
| + | The partially ordered set $ S $ | ||
| + | is called subspace-finite if there are only finitely many isomorphism classes of indecomposable $ S $- | ||
| + | spaces. Kleiner's theorem asserts that $ S $ | ||
| + | is subspace-finite if $ S $ | ||
| + | is finite and does not contain as a full subset one of the partially ordered sets | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r081400a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r081400a.gif" /> | ||
Latest revision as of 08:11, 6 June 2020
Let $ S $
be a partially ordered set and $ k $
a field. Let $ \omega $
be a symbol with $ \omega \notin S $.
An $ S $-
space is of the form $ V=( V _ \omega , V _ {s} ) _ {s \in S } $,
where the $ V _ {s} $
are subspaces of the $ k $-
space $ V _ \omega $
for $ s \in S $,
such that $ s \leq s ^ \prime $
implies $ V _ {s} \subset V _ {s ^ \prime } $.
Let $ V , V ^ \prime $
be $ S $-
spaces; a mapping $ f: V \rightarrow V ^ \prime $
is a $ k $-
linear mapping $ V _ \omega \rightarrow V _ \omega ^ \prime $
such that $ f( V _ {s} ) \subset V _ {s} ^ \prime $
for all $ s \in S $.
The direct sum of $ V $
and $ V ^ \prime $
is $ V \oplus V ^ \prime $
with $ ( V \oplus V ^ \prime ) _ {s} = V _ {s} \oplus V _ {s} ^ \prime $
for all $ s \in S \cup \{ \omega \} $.
An $ S $-
space is said to be indecomposable if it cannot be written as the direct sum of two non-zero $ S $-
spaces.
The partially ordered set $ S $ is called subspace-finite if there are only finitely many isomorphism classes of indecomposable $ S $- spaces. Kleiner's theorem asserts that $ S $ is subspace-finite if $ S $ is finite and does not contain as a full subset one of the partially ordered sets
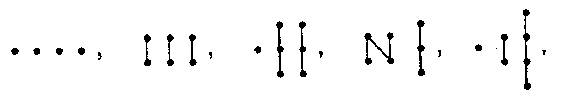
Figure: r081400a
see [a1]. M.M. Kleiner also has determined all the indecomposable representations of a representation-finite partially ordered set [a2]. A characterization of the tame partially ordered sets has been obtained by L.A. Nazarova [a3]. The representation theory of partially ordered sets plays a prominent role in the representation theory of finite-dimensional algebras.
References
| [a1] | M.M. Kleiner, "Partially ordered sets of finite type" J. Soviet Math. , 3 (1975) pp. 607–615 Zap. Nauchn. Sem. Leningr. Otdel. Mat. Inst. , 28 (1972) pp. 32–41 |
| [a2] | M.M. Kleiner, "On the exact representations of partially ordered sets of finite type" J. Soviet Math. , 3 (1975) pp. 616–628 Zap. Nauchn. Sem. Leningr. Otdel. Mat. Inst. , 28 (1972) pp. 42–60 |
| [a3] | L.A. Nazarova, "Partially ordered sets of infinite type" Math. USSR Izv. , 9 : 5 (1975) pp. 911–938 Izv. Akad. Nauk SSSR Ser. Mat. , 39 (1975) pp. 963–991 |
How to Cite This Entry:
Representation of a partially ordered set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Representation_of_a_partially_ordered_set&oldid=18218
Representation of a partially ordered set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Representation_of_a_partially_ordered_set&oldid=18218
This article was adapted from an original article by C.M. Ringel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article