Difference between revisions of "Quasi-equivalent representations"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | Two unitary representations (cf. [[Unitary representation|Unitary representation]]) | + | <!-- |
| + | q0764801.png | ||
| + | $#A+1 = 38 n = 1 | ||
| + | $#C+1 = 38 : ~/encyclopedia/old_files/data/Q076/Q.0706480 Quasi\AAhequivalent representations | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | Two unitary representations (cf. [[Unitary representation|Unitary representation]]) $ \pi _ {1} , \pi _ {2} $ | ||
| + | of a group $ X $( | ||
| + | or symmetric representations of a symmetric algebra $ X $) | ||
| + | in Hilbert spaces $ H _ {1} $ | ||
| + | and $ H _ {2} $, | ||
| + | respectively, satisfying one of the following four equivalent conditions: 1) there exist unitarily-equivalent representations $ \rho _ {1} $ | ||
| + | and $ \rho _ {2} $ | ||
| + | such that $ \rho _ {1} $ | ||
| + | is a multiple of $ \pi _ {1} $ | ||
| + | and $ \rho _ {2} $ | ||
| + | is a multiple of $ \pi _ {2} $; | ||
| + | 2) the non-zero subrepresentations of $ \pi _ {1} $ | ||
| + | are not disjoint from $ \pi _ {2} $, | ||
| + | and the non-zero subrepresentations of $ \pi _ {2} $ | ||
| + | are not disjoint from $ \pi _ {1} $; | ||
| + | 3) $ \pi _ {2} $ | ||
| + | is unitarily equivalent to a subrepresentation of some multiple representation $ \rho _ {1} $ | ||
| + | of $ \pi _ {1} $ | ||
| + | that has unit central support; or 4) there exists an isomorphism $ \Phi $ | ||
| + | of the [[Von Neumann algebra|von Neumann algebra]] generated by the set $ \pi _ {1} ( X) $ | ||
| + | onto the von Neumann algebra generated by the set $ \pi _ {2} ( X) $ | ||
| + | such that $ \Phi ( \pi _ {1} ( x) ) = \pi _ {2} ( x) $ | ||
| + | for all $ x \in X $. | ||
| + | Unitarily-equivalent representations are quasi-equivalent representations; irreducible quasi-equivalent representations (cf. [[Irreducible representation|Irreducible representation]]) are unitarily equivalent. If $ \pi _ {1} $ | ||
| + | and $ \pi _ {2} $ | ||
| + | are quasi-equivalent representations and $ \pi _ {1} $ | ||
| + | is a [[Factor representation|factor representation]], then so is $ \pi _ {2} $; | ||
| + | a factor representation and a non-zero subrepresentation of it are quasi-equivalent representations; two factor representations are either disjoint or quasi-equivalent. The notion of quasi-equivalent representations leads to that of a quasi-dual object and a quasi-spectrum for locally compact groups and symmetric algebras, respectively. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Dixmier, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076480/q07648028.png" /> algebras" , North-Holland (1977) (Translated from French)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Dixmier, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076480/q07648028.png" /> algebras" , North-Holland (1977) (Translated from French)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | Two representations | + | Two representations $ \pi $ |
| + | and $ \pi ^ \prime $( | ||
| + | of a group or algebra) with representation spaces $ H $ | ||
| + | and $ H ^ \prime $, | ||
| + | respectively, are said to be disjoint is there is no non-zero intertwining operator between $ \pi $ | ||
| + | and $ \pi ^ \prime $. | ||
| + | Here, an intertwining operator between $ \pi $ | ||
| + | and $ \pi ^ \prime $ | ||
| + | is a continuous linear operator $ T : H \rightarrow H ^ \prime $ | ||
| + | such that $ T \pi ( x) = \pi ^ \prime T ( x) $ | ||
| + | for all $ x $. | ||
Latest revision as of 08:09, 6 June 2020
Two unitary representations (cf. Unitary representation) $ \pi _ {1} , \pi _ {2} $
of a group $ X $(
or symmetric representations of a symmetric algebra $ X $)
in Hilbert spaces $ H _ {1} $
and $ H _ {2} $,
respectively, satisfying one of the following four equivalent conditions: 1) there exist unitarily-equivalent representations $ \rho _ {1} $
and $ \rho _ {2} $
such that $ \rho _ {1} $
is a multiple of $ \pi _ {1} $
and $ \rho _ {2} $
is a multiple of $ \pi _ {2} $;
2) the non-zero subrepresentations of $ \pi _ {1} $
are not disjoint from $ \pi _ {2} $,
and the non-zero subrepresentations of $ \pi _ {2} $
are not disjoint from $ \pi _ {1} $;
3) $ \pi _ {2} $
is unitarily equivalent to a subrepresentation of some multiple representation $ \rho _ {1} $
of $ \pi _ {1} $
that has unit central support; or 4) there exists an isomorphism $ \Phi $
of the von Neumann algebra generated by the set $ \pi _ {1} ( X) $
onto the von Neumann algebra generated by the set $ \pi _ {2} ( X) $
such that $ \Phi ( \pi _ {1} ( x) ) = \pi _ {2} ( x) $
for all $ x \in X $.
Unitarily-equivalent representations are quasi-equivalent representations; irreducible quasi-equivalent representations (cf. Irreducible representation) are unitarily equivalent. If $ \pi _ {1} $
and $ \pi _ {2} $
are quasi-equivalent representations and $ \pi _ {1} $
is a factor representation, then so is $ \pi _ {2} $;
a factor representation and a non-zero subrepresentation of it are quasi-equivalent representations; two factor representations are either disjoint or quasi-equivalent. The notion of quasi-equivalent representations leads to that of a quasi-dual object and a quasi-spectrum for locally compact groups and symmetric algebras, respectively.
References
| [1] | J. Dixmier, "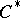 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
Comments
Two representations $ \pi $ and $ \pi ^ \prime $( of a group or algebra) with representation spaces $ H $ and $ H ^ \prime $, respectively, are said to be disjoint is there is no non-zero intertwining operator between $ \pi $ and $ \pi ^ \prime $. Here, an intertwining operator between $ \pi $ and $ \pi ^ \prime $ is a continuous linear operator $ T : H \rightarrow H ^ \prime $ such that $ T \pi ( x) = \pi ^ \prime T ( x) $ for all $ x $.
Quasi-equivalent representations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-equivalent_representations&oldid=11441