Difference between revisions of "Prüfer domain"
Ulf Rehmann (talk | contribs) m (moved Prüfer domain to Pruefer domain: ascii title) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | p1102601.png | ||
| + | $#A+1 = 6 n = 2 | ||
| + | $#C+1 = 6 : ~/encyclopedia/old_files/data/P110/P.1100260 Pr\AGufer domain | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | ii) an | + | A commutative semi-hereditary [[Integral domain|integral domain]] (cf. also [[Semi-hereditary ring|Semi-hereditary ring]]; [[Injective module|Injective module]]). The Prüfer domains are the commutative integral domains $ A $ |
| + | that satisfy the following two conditions: | ||
| + | |||
| + | i) the localization $ A _ {\mathcal M} $( | ||
| + | cf. also [[Localization in a commutative algebra|Localization in a commutative algebra]]) is a valuation ring (see [[Valuation|Valuation]]) for every maximal ideal $ {\mathcal M} $ | ||
| + | of $ A $; | ||
| + | |||
| + | ii) an $ A $- | ||
| + | module $ M $ | ||
| + | is flat (cf. [[Flat module|Flat module]]) if and only if it is torsion-free (cf. also [[Group without torsion|Group without torsion]]). | ||
A Noetherian Prüfer domain is a Dedekind domain (see [[Dedekind ring|Dedekind ring]]). Each Bezout domain (also called [[Bezout ring|Bezout ring]]) is a Prüfer domain. | A Noetherian Prüfer domain is a Dedekind domain (see [[Dedekind ring|Dedekind ring]]). Each Bezout domain (also called [[Bezout ring|Bezout ring]]) is a Prüfer domain. | ||
Latest revision as of 08:08, 6 June 2020
A commutative semi-hereditary integral domain (cf. also Semi-hereditary ring; Injective module). The Prüfer domains are the commutative integral domains $ A $
that satisfy the following two conditions:
i) the localization $ A _ {\mathcal M} $( cf. also Localization in a commutative algebra) is a valuation ring (see Valuation) for every maximal ideal $ {\mathcal M} $ of $ A $;
ii) an $ A $- module $ M $ is flat (cf. Flat module) if and only if it is torsion-free (cf. also Group without torsion).
A Noetherian Prüfer domain is a Dedekind domain (see Dedekind ring). Each Bezout domain (also called Bezout ring) is a Prüfer domain.
There are Prüfer domains that are not Bezout and there are Prüfer domains having finitely generated ideals requiring more than two generators [a2] (hence, these are not Dedekind rings).
References
| [a1] | R. Gilmer, "Multiplicative ideal theory" , M. Dekker (1972) |
| [a2] | R. Heidman, L. Levy, "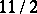 and and  -generator ideals in Prüfer domains" Rocky Mount. Math. J. , 5 (1975) pp. 361–373 -generator ideals in Prüfer domains" Rocky Mount. Math. J. , 5 (1975) pp. 361–373 |
| [a3] | H.C. Hutchins, "Examples of commutative rings" , Polygonal (1981) |
Prüfer domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pr%C3%BCfer_domain&oldid=22955