Difference between revisions of "Polar decomposition"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | A | + | <!-- |
| + | p0734301.png | ||
| + | $#A+1 = 88 n = 1 | ||
| + | $#C+1 = 88 : ~/encyclopedia/old_files/data/P073/P.0703430 Polar decomposition | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A polar decomposition of a linear transformation on a finite-dimensional Euclidean (or unitary) space $ L $ | |
| + | is a decomposition of the [[Linear transformation|linear transformation]] into a product of a self-adjoint and an orthogonal (respectively, unitary) transformation (cf. [[Orthogonal transformation|Orthogonal transformation]]; [[Self-adjoint linear transformation|Self-adjoint linear transformation]]; [[Unitary transformation|Unitary transformation]]). Any linear transformation $ A $ | ||
| + | on $ L $ | ||
| + | has a polar decomposition | ||
| + | |||
| + | $$ | ||
| + | A = S \cdot U , | ||
| + | $$ | ||
| + | |||
| + | where $ S $ | ||
| + | is a positive semi-definite self-adjoint linear transformation and $ U $ | ||
| + | is an orthogonal (or unitary) linear transformation; moreover, $ S $ | ||
| + | is uniquely defined. If $ A $ | ||
| + | is non-degenerate, then $ S $ | ||
| + | is even positive definite and $ U $ | ||
| + | is also uniquely defined. A polar decomposition on a one-dimensional unitary space coincides with the trigonometric representation of a complex number $ z $ | ||
| + | as $ z = re ^ {i \phi } $. | ||
''A.L. Onishchik'' | ''A.L. Onishchik'' | ||
| − | A polar decomposition of an operator | + | A polar decomposition of an operator $ A $ |
| + | acting on a [[Hilbert space|Hilbert space]] is a representation of $ A $ | ||
| + | in the form | ||
| − | + | $$ | |
| + | A = U T, | ||
| + | $$ | ||
| − | where | + | where $ U $ |
| + | is a partial [[Isometric operator|isometric operator]] and $ T $ | ||
| + | is a [[Positive operator|positive operator]]. Any closed operator $ A $ | ||
| + | has a polar decomposition, moreover, $ T = ( A ^ {*} A ) ^ {1/2} $( | ||
| + | which is often denoted by $ T = | A | $), | ||
| + | and $ U $ | ||
| + | maps the closure $ \overline{R}\; _ {A ^ {*} } $ | ||
| + | of the domain of the self-adjoint operator $ A $ | ||
| + | into the closure $ \overline{R}\; _ {A} $ | ||
| + | of the range of $ A $( | ||
| + | the von Neumann theorem, see ). A polar decomposition becomes unique if the source and target subspaces of $ U $ | ||
| + | are required to coincide with $ \overline{R}\; _ {A ^ {*} } $ | ||
| + | and $ \overline{R}\; _ {A} $, | ||
| + | respectively. On the other hand, $ U $ | ||
| + | can be always chosen unitary, isometric or co-isometric, depending on the relation between the codimensions of the subspaces $ \overline{R}\; _ {A ^ {*} } $ | ||
| + | and $ \overline{R}\; _ {A} $. | ||
| + | In particular, if | ||
| − | + | $$ | |
| + | \mathop{\rm dim} H \ominus \overline{R}\; _ {A ^ {*} } = \ | ||
| + | \mathop{\rm dim} H \ominus \overline{R}\; _ {A} , | ||
| + | $$ | ||
| − | then | + | then $ U $ |
| + | can be chosen unitary and there is a Hermitian operator $ \Phi $ | ||
| + | such that $ U = \mathop{\rm exp} ( i \Phi ) $. | ||
| + | Then the polar decomposition of $ A $ | ||
| + | takes the form | ||
| − | + | $$ | |
| + | A = \mathop{\rm exp} ( i \Phi ) | A | , | ||
| + | $$ | ||
entirely analogous to the polar decomposition of a complex number. Commutativity of the terms in a polar decomposition takes place if and only if the operator is normal (cf. [[Normal operator|Normal operator]]). | entirely analogous to the polar decomposition of a complex number. Commutativity of the terms in a polar decomposition takes place if and only if the operator is normal (cf. [[Normal operator|Normal operator]]). | ||
| Line 23: | Line 76: | ||
An expression analogous to the polar decomposition has been obtained for operators on a [[Space with an indefinite metric|space with an indefinite metric]] (see , ). | An expression analogous to the polar decomposition has been obtained for operators on a [[Space with an indefinite metric|space with an indefinite metric]] (see , ). | ||
| − | A polar decomposition of a functional on a von Neumann algebra | + | A polar decomposition of a functional on a von Neumann algebra $ A $ |
| + | is a representation of a normal functional $ f $ | ||
| + | on $ A $ | ||
| + | in the form $ f = u p $, | ||
| + | where $ p $ | ||
| + | is a positive normal functional on $ A $, | ||
| + | $ u \in A $ | ||
| + | is a partial isometry (i.e. $ u ^ {*} u $ | ||
| + | and $ u u ^ {*} $ | ||
| + | are projectors), and multiplication is understood as the action on $ p $ | ||
| + | of the operator which is adjoint to left multiplication by $ u $ | ||
| + | in $ A $: | ||
| + | $ f ( x) = p ( u x ) $ | ||
| + | for all $ x \in A $. | ||
| + | A polar decomposition can always be realized so that the condition $ u ^ {*} f = p $ | ||
| + | is fulfilled. Under this condition a polar decomposition is unique. | ||
| − | Any bounded linear functional | + | Any bounded linear functional $ f $ |
| + | on an arbitrary [[C*-algebra| $ C ^ {*} $- | ||
| + | algebra]] $ A $ | ||
| + | can be considered as a normal functional on the universal enveloping [[Von Neumann algebra|von Neumann algebra]] $ A ^ {\prime\prime} $; | ||
| + | the corresponding polar decomposition $ f = u p $ | ||
| + | is called the enveloping polar decomposition of the functional $ f $. | ||
| + | The restriction of the functional $ p $ | ||
| + | to $ A $ | ||
| + | is called the absolute value of $ f $ | ||
| + | and is denoted by $ | f | $; | ||
| + | the following properties determine the functional $ | f | $ | ||
| + | uniquely: | ||
| − | + | $$ | |
| + | \| | f | \| = \| f \| | ||
| + | \ \textrm{ and } \ | f ( x) | ^ {2} \leq \| f | ||
| + | \| \cdot | f | ( x ^ {*} x ) . | ||
| + | $$ | ||
| − | In the case when | + | In the case when $ A = C ( X) $ |
| + | is the algebra of all continuous functions on a compactum, the absolute value of a functional corresponds to the total variation of the measure determined by it (cf. also [[Total variation of a function|Total variation of a function]]). | ||
| − | In many cases a polar decomposition of a functional allows one to reduce studies of functionals on | + | In many cases a polar decomposition of a functional allows one to reduce studies of functionals on $ C ^ {*} $- |
| + | algebras to studies of positive functionals. It enables one, for example, to construct for each $ f \in A ^ \prime $ | ||
| + | a representation $ \pi $ | ||
| + | of the algebra $ A $ | ||
| + | on which $ f $ | ||
| + | has a vector realization (i.e. there are vectors $ \xi , \eta $ | ||
| + | in $ H _ \pi $ | ||
| + | such that $ f ( x) = ( \pi ( x) \xi , \eta ) $, | ||
| + | $ x \in A $). | ||
| + | The representation $ \pi _ {| f | } $ | ||
| + | constructed from the positive functional $ | f | $ | ||
| + | using the GNS-construction (of Gel'fand–Naimark–Segal) has that property. | ||
| − | The polar decomposition of an element of a | + | The polar decomposition of an element of a $ C ^ {*} $- |
| + | algebra is a representation of the element as the product of a positive element and a partial isometric element. Polar decomposition is not valid for all elements: in the usual polar decomposition of an operator $ T $ | ||
| + | on a Hilbert space the positive term belongs to the $ C ^ {*} $- | ||
| + | algebra generated by $ T $, | ||
| + | but for the partial isometric term one can only state that it belongs to the von Neumann algebra generated by $ T $. | ||
| + | That is why one defines and uses the so-called enveloping polar decomposition of an element $ a \in A $: | ||
| + | $ a = u t $, | ||
| + | where $ t = ( a ^ {*} a ) ^ {1/2} \in A $ | ||
| + | and $ u $ | ||
| + | is a partial isometric element in the universal enveloping von Neumann algebra $ A ^ {\prime\prime} $( | ||
| + | it is assumed that $ A $ | ||
| + | is canonically imbedded in $ A ^ {\prime\prime} $). | ||
====References==== | ====References==== | ||
| Line 41: | Line 147: | ||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> I.C. [I.Ts. Gokhberg] Gohberg, M.G. Krein, "Introduction to the theory of linear nonselfadjoint operators" , ''Transl. Math. Monogr.'' , '''18''' , Amer. Math. Soc. (1969) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> I.C. [I.Ts. Gokhberg] Gohberg, M.G. Krein, "Introduction to the theory of linear nonselfadjoint operators" , ''Transl. Math. Monogr.'' , '''18''' , Amer. Math. Soc. (1969) (Translated from Russian)</TD></TR></table> | ||
Latest revision as of 08:06, 6 June 2020
A polar decomposition of a linear transformation on a finite-dimensional Euclidean (or unitary) space $ L $
is a decomposition of the linear transformation into a product of a self-adjoint and an orthogonal (respectively, unitary) transformation (cf. Orthogonal transformation; Self-adjoint linear transformation; Unitary transformation). Any linear transformation $ A $
on $ L $
has a polar decomposition
$$ A = S \cdot U , $$
where $ S $ is a positive semi-definite self-adjoint linear transformation and $ U $ is an orthogonal (or unitary) linear transformation; moreover, $ S $ is uniquely defined. If $ A $ is non-degenerate, then $ S $ is even positive definite and $ U $ is also uniquely defined. A polar decomposition on a one-dimensional unitary space coincides with the trigonometric representation of a complex number $ z $ as $ z = re ^ {i \phi } $.
A.L. Onishchik
A polar decomposition of an operator $ A $ acting on a Hilbert space is a representation of $ A $ in the form
$$ A = U T, $$
where $ U $ is a partial isometric operator and $ T $ is a positive operator. Any closed operator $ A $ has a polar decomposition, moreover, $ T = ( A ^ {*} A ) ^ {1/2} $( which is often denoted by $ T = | A | $), and $ U $ maps the closure $ \overline{R}\; _ {A ^ {*} } $ of the domain of the self-adjoint operator $ A $ into the closure $ \overline{R}\; _ {A} $ of the range of $ A $( the von Neumann theorem, see ). A polar decomposition becomes unique if the source and target subspaces of $ U $ are required to coincide with $ \overline{R}\; _ {A ^ {*} } $ and $ \overline{R}\; _ {A} $, respectively. On the other hand, $ U $ can be always chosen unitary, isometric or co-isometric, depending on the relation between the codimensions of the subspaces $ \overline{R}\; _ {A ^ {*} } $ and $ \overline{R}\; _ {A} $. In particular, if
$$ \mathop{\rm dim} H \ominus \overline{R}\; _ {A ^ {*} } = \ \mathop{\rm dim} H \ominus \overline{R}\; _ {A} , $$
then $ U $ can be chosen unitary and there is a Hermitian operator $ \Phi $ such that $ U = \mathop{\rm exp} ( i \Phi ) $. Then the polar decomposition of $ A $ takes the form
$$ A = \mathop{\rm exp} ( i \Phi ) | A | , $$
entirely analogous to the polar decomposition of a complex number. Commutativity of the terms in a polar decomposition takes place if and only if the operator is normal (cf. Normal operator).
An expression analogous to the polar decomposition has been obtained for operators on a space with an indefinite metric (see , ).
A polar decomposition of a functional on a von Neumann algebra $ A $ is a representation of a normal functional $ f $ on $ A $ in the form $ f = u p $, where $ p $ is a positive normal functional on $ A $, $ u \in A $ is a partial isometry (i.e. $ u ^ {*} u $ and $ u u ^ {*} $ are projectors), and multiplication is understood as the action on $ p $ of the operator which is adjoint to left multiplication by $ u $ in $ A $: $ f ( x) = p ( u x ) $ for all $ x \in A $. A polar decomposition can always be realized so that the condition $ u ^ {*} f = p $ is fulfilled. Under this condition a polar decomposition is unique.
Any bounded linear functional $ f $ on an arbitrary $ C ^ {*} $- algebra $ A $ can be considered as a normal functional on the universal enveloping von Neumann algebra $ A ^ {\prime\prime} $; the corresponding polar decomposition $ f = u p $ is called the enveloping polar decomposition of the functional $ f $. The restriction of the functional $ p $ to $ A $ is called the absolute value of $ f $ and is denoted by $ | f | $; the following properties determine the functional $ | f | $ uniquely:
$$ \| | f | \| = \| f \| \ \textrm{ and } \ | f ( x) | ^ {2} \leq \| f \| \cdot | f | ( x ^ {*} x ) . $$
In the case when $ A = C ( X) $ is the algebra of all continuous functions on a compactum, the absolute value of a functional corresponds to the total variation of the measure determined by it (cf. also Total variation of a function).
In many cases a polar decomposition of a functional allows one to reduce studies of functionals on $ C ^ {*} $- algebras to studies of positive functionals. It enables one, for example, to construct for each $ f \in A ^ \prime $ a representation $ \pi $ of the algebra $ A $ on which $ f $ has a vector realization (i.e. there are vectors $ \xi , \eta $ in $ H _ \pi $ such that $ f ( x) = ( \pi ( x) \xi , \eta ) $, $ x \in A $). The representation $ \pi _ {| f | } $ constructed from the positive functional $ | f | $ using the GNS-construction (of Gel'fand–Naimark–Segal) has that property.
The polar decomposition of an element of a $ C ^ {*} $- algebra is a representation of the element as the product of a positive element and a partial isometric element. Polar decomposition is not valid for all elements: in the usual polar decomposition of an operator $ T $ on a Hilbert space the positive term belongs to the $ C ^ {*} $- algebra generated by $ T $, but for the partial isometric term one can only state that it belongs to the von Neumann algebra generated by $ T $. That is why one defines and uses the so-called enveloping polar decomposition of an element $ a \in A $: $ a = u t $, where $ t = ( a ^ {*} a ) ^ {1/2} \in A $ and $ u $ is a partial isometric element in the universal enveloping von Neumann algebra $ A ^ {\prime\prime} $( it is assumed that $ A $ is canonically imbedded in $ A ^ {\prime\prime} $).
References
| [1] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
| [2] | J. Bognár, "Certain relations among the non-negativity properties of operators on spaces with an indefinite metric II" Stud. Scient. Math. Hung. , 1 : 1–2 (1966) pp. 97–102 (In Russian) |
| [3] | J. Dixmier, "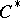 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
V.S. Shul'man
Comments
References
| [a1] | I.C. [I.Ts. Gokhberg] Gohberg, M.G. Krein, "Introduction to the theory of linear nonselfadjoint operators" , Transl. Math. Monogr. , 18 , Amer. Math. Soc. (1969) (Translated from Russian) |
Polar decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polar_decomposition&oldid=16949