Difference between revisions of "Oscillating differential equation"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | o0704701.png | ||
| + | $#A+1 = 52 n = 5 | ||
| + | $#C+1 = 52 : ~/encyclopedia/old_files/data/O070/O.0700470 Oscillating differential equation | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | An ordinary differential equation which has at least one [[Oscillating solution|oscillating solution]]. There are different concepts of the oscillation of a solution. The most widespread are oscillation at a point (usually taken to be $ + \infty $) | |
| + | and oscillation on an interval. A non-zero solution of the equation | ||
| − | + | $$ \tag{1 } | |
| + | u ^ {(} n) = f( t, u , u ^ \prime \dots u ^ {(} n- 1) ),\ n \geq 2 , | ||
| + | $$ | ||
| − | + | where $ f( t, 0 \dots 0) = 0 $, | |
| + | is called oscillating at the point $ + \infty $( | ||
| + | or on an interval $ I $) | ||
| + | if it has a sequence of zeros which converges to $ + \infty $( | ||
| + | respectively, there are at least $ n $ | ||
| + | zeros in $ I $ | ||
| + | counted according to their multiplicity). Equation (1) is oscillating at $ + \infty $ | ||
| + | or on an interval $ I $ | ||
| + | if its solutions are oscillating (at $ + \infty $, | ||
| + | respectively, on $ I $). | ||
| − | are | + | Among equations which are oscillatory at $ + \infty $ |
| + | the equations which possess the properties $ A $ | ||
| + | or $ B $, | ||
| + | i.e. which are compatible in a specific sense with one of the equations | ||
| − | + | $$ | |
| + | u ^ {(} n) = - u \ \textrm{ or } \ u ^ {(} n) = u , | ||
| + | $$ | ||
| − | + | are distinguished. Equation (1) is said to possess property $ A $ | |
| + | if all its solutions defined in a neighbourhood of $ + \infty $ | ||
| + | are oscillating when $ n $ | ||
| + | is even; when $ n $ | ||
| + | is odd, they should either be oscillating or satisfy the condition | ||
| − | + | $$ \tag{2 } | |
| + | \lim\limits _ {t \rightarrow + \infty } u ^ {(} i- 1) ( t) = 0,\ i = 1 \dots n. | ||
| + | $$ | ||
| − | + | If every solution of equation (1) defined in a neighbourhood of $ + \infty $, | |
| + | when $ n $ | ||
| + | is even, is either oscillating, or satisfies condition (2) or | ||
| + | |||
| + | $$ \tag{3 } | ||
| + | \lim\limits _ {t \rightarrow + \infty } | u ^ {(} i- 1) ( t) | = + \infty ,\ \ | ||
| + | i = 1 \dots n, | ||
| + | $$ | ||
| + | |||
| + | while when $ n $ | ||
| + | is odd, it is either oscillating or satisfies condition (3), then the equation possesses property $ B $. | ||
The linear equation | The linear equation | ||
| − | + | $$ \tag{4 } | |
| + | u ^ {(} n) = a( t) u | ||
| + | $$ | ||
| − | with a locally summable coefficient | + | with a locally summable coefficient $ a: [ t _ {0} , + \infty ) \rightarrow \mathbf R $ |
| + | possesses property $ A $( | ||
| + | property $ B $) | ||
| + | if | ||
| − | + | $$ | |
| + | a( t) \leq 0 \ ( a( t) \geq 0) \ \textrm{ when } t \geq t _ {0} $$ | ||
and either | and either | ||
| − | + | $$ | |
| + | \int\limits _ {t _ {0} } ^ { {+ } \infty } t ^ {n- 1- \epsilon } | a( t) | dt = + \infty | ||
| + | $$ | ||
or | or | ||
| − | + | $$ | |
| + | a( t) \leq | ||
| + | \frac{\mu _ {n} - \epsilon }{t ^ {n} } | ||
| + | \ \left ( a( t) \geq | ||
| + | \frac{\nu _ {n} + \epsilon }{t ^ {n} } | ||
| + | \right ) | ||
| + | $$ | ||
| − | when | + | when $ t \geq t _ {0} $, |
| + | where $ \epsilon > 0 $ | ||
| + | and $ \mu _ {n} $ | ||
| + | is the smallest ( $ \nu _ {n} $ | ||
| + | is the largest) of the local minima (maxima) of the polynomial $ x( x- 1) \dots ( x- n+ 1) $( | ||
| + | see [[#References|[1]]]–[[#References|[5]]]). | ||
An equation of Emden–Fowler type | An equation of Emden–Fowler type | ||
| − | + | $$ \tag{5 } | |
| + | u ^ {(} n) = a( t) | u | ^ \lambda \mathop{\rm sign} u ,\ \ | ||
| + | \lambda > 0,\ \lambda \neq 1, | ||
| + | $$ | ||
| − | with a locally summable non-positive (non-negative) coefficient | + | with a locally summable non-positive (non-negative) coefficient $ a: [ t _ {0} , + \infty ) \rightarrow \mathbf R $ |
| + | possesses property $ A $( | ||
| + | property $ B $) | ||
| + | if and only if | ||
| − | + | $$ | |
| + | \int\limits _ {t _ {0} } ^ { {+ } \infty } t ^ \mu | a( t) | dt = + \infty , | ||
| + | $$ | ||
| − | where | + | where $ \mu = \min \{ n- 1, ( n- 1) \lambda \} $( |
| + | see [[#References|[4]]], [[#References|[6]]], [[#References|[7]]]). | ||
In a number of cases the question of the oscillation of equation (1) can be reduced to the same question for the standard equations of the form (4) and (5) using a [[Comparison theorem|comparison theorem]] (see [[#References|[11]]]). | In a number of cases the question of the oscillation of equation (1) can be reduced to the same question for the standard equations of the form (4) and (5) using a [[Comparison theorem|comparison theorem]] (see [[#References|[11]]]). | ||
| − | In studying the oscillatory properties of equations with deviating argument, certain specific features arise. For example, if | + | In studying the oscillatory properties of equations with deviating argument, certain specific features arise. For example, if $ n $ |
| + | is odd, $ \Delta > 0 $, | ||
| + | and if for large $ t $ | ||
| + | the inequality | ||
| − | < | + | $$ |
| + | a( t) \leq a _ {0} < - n! \Delta ^ {-} n | ||
| + | $$ | ||
is fulfilled, then all non-zero solutions of the equation | is fulfilled, then all non-zero solutions of the equation | ||
| − | + | $$ | |
| + | u ^ {(} n) ( t) = a( t) u( t - \Delta ) | ||
| + | $$ | ||
| − | are oscillatory at | + | are oscillatory at $ + \infty $( |
| + | see [[#References|[10]]], [[#References|[11]]]). At the same time, if $ a $ | ||
| + | is non-positive and $ n $ | ||
| + | is odd, the non-retarded equation (4) always has a non-oscillating solution. | ||
The concepts of oscillation and non-oscillation on an interval are generally studied for linear homogeneous equations. They are of fundamental value in the theory of boundary value problems (see [[#References|[12]]]). | The concepts of oscillation and non-oscillation on an interval are generally studied for linear homogeneous equations. They are of fundamental value in the theory of boundary value problems (see [[#References|[12]]]). | ||
| Line 63: | Line 142: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Kneser, "Untersuchungen über die reellen Nullstellen der Integrale linearer Integralgleichungen" ''Math. Ann.'' , '''42''' (1893) pp. 409–435</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.G. Mikusinksi, "On Fite's oscillation theorems" ''Colloq. Math.'' , '''2''' (1951) pp. 34–39</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.A. Kondrat'ev, "The oscillatory character of solutions of the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070470/o07047056.png" />" ''Trudy Moskov. Mat. Obshch.'' , '''10''' (1961) pp. 419–436 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> I.T. Kiguradze, "On the oscillatory character of solutions of the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070470/o07047057.png" />" ''Mat. Sb.'' , '''65''' : 2 (1964) pp. 172–187 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> T.A. Chanturiya, "On a comparison theorem for linear differential equations" ''Math. USSR Izv.'' , '''10''' : 5 (1976) pp. 1075–1088 ''Izv. Akad. Nauk. SSSR Ser. Mat.'' , '''40''' : 5 (1976) pp. 1128–1142</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> I. Ličko, M. Švec, "La charactère oscillatoire des solutions de l'équation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070470/o07047058.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070470/o07047059.png" />" ''Chekhosl. Mat. Zh.'' , '''13''' (1963) pp. 481–491</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> I.T. Kiguradze, "On the oscillatory and monotone solutions of ordinary differential equations" ''Arch. Math.'' , '''14''' : 1 (1978) pp. 21–44</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> C.A. Swanson, "Comparison and oscillation theory of linear differential equations" , Acad. Press (1968)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> P. Hartman, "Ordinary differential equations" , Birkhäuser (1982)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> A.D. Myshkis, "Linear differential equations with retarded argument" , Moscow (1972) (In Russian)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> R.G. Koplatadze, T.A. Chanturiya, "On the oscillatory properties of differential equations with deviating argument" , Tbilisi (1977) (In Russian)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> A.Yu. Levin, "Non-oscillation of the solutions of the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070470/o07047060.png" />" ''Russian Math. Surveys'' , '''24''' : 2 (1969) pp. 43–99 ''Uspekhi Mat. Nauk'' , '''24''' : 2 (1969) pp. 43–96</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Kneser, "Untersuchungen über die reellen Nullstellen der Integrale linearer Integralgleichungen" ''Math. Ann.'' , '''42''' (1893) pp. 409–435</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.G. Mikusinksi, "On Fite's oscillation theorems" ''Colloq. Math.'' , '''2''' (1951) pp. 34–39</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.A. Kondrat'ev, "The oscillatory character of solutions of the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070470/o07047056.png" />" ''Trudy Moskov. Mat. Obshch.'' , '''10''' (1961) pp. 419–436 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> I.T. Kiguradze, "On the oscillatory character of solutions of the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070470/o07047057.png" />" ''Mat. Sb.'' , '''65''' : 2 (1964) pp. 172–187 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> T.A. Chanturiya, "On a comparison theorem for linear differential equations" ''Math. USSR Izv.'' , '''10''' : 5 (1976) pp. 1075–1088 ''Izv. Akad. Nauk. SSSR Ser. Mat.'' , '''40''' : 5 (1976) pp. 1128–1142</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> I. Ličko, M. Švec, "La charactère oscillatoire des solutions de l'équation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070470/o07047058.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070470/o07047059.png" />" ''Chekhosl. Mat. Zh.'' , '''13''' (1963) pp. 481–491</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> I.T. Kiguradze, "On the oscillatory and monotone solutions of ordinary differential equations" ''Arch. Math.'' , '''14''' : 1 (1978) pp. 21–44</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> C.A. Swanson, "Comparison and oscillation theory of linear differential equations" , Acad. Press (1968)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> P. Hartman, "Ordinary differential equations" , Birkhäuser (1982)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> A.D. Myshkis, "Linear differential equations with retarded argument" , Moscow (1972) (In Russian)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> R.G. Koplatadze, T.A. Chanturiya, "On the oscillatory properties of differential equations with deviating argument" , Tbilisi (1977) (In Russian)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> A.Yu. Levin, "Non-oscillation of the solutions of the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070470/o07047060.png" />" ''Russian Math. Surveys'' , '''24''' : 2 (1969) pp. 43–99 ''Uspekhi Mat. Nauk'' , '''24''' : 2 (1969) pp. 43–96</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.K. Hale, "Ordinary differential equations" , Wiley (1969)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W.T. Reid, "Sturmian theory for ordinary differential equations" , Springer (1980)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.K. Hale, "Ordinary differential equations" , Wiley (1969)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W.T. Reid, "Sturmian theory for ordinary differential equations" , Springer (1980)</TD></TR></table> | ||
Latest revision as of 08:04, 6 June 2020
An ordinary differential equation which has at least one oscillating solution. There are different concepts of the oscillation of a solution. The most widespread are oscillation at a point (usually taken to be $ + \infty $)
and oscillation on an interval. A non-zero solution of the equation
$$ \tag{1 } u ^ {(} n) = f( t, u , u ^ \prime \dots u ^ {(} n- 1) ),\ n \geq 2 , $$
where $ f( t, 0 \dots 0) = 0 $, is called oscillating at the point $ + \infty $( or on an interval $ I $) if it has a sequence of zeros which converges to $ + \infty $( respectively, there are at least $ n $ zeros in $ I $ counted according to their multiplicity). Equation (1) is oscillating at $ + \infty $ or on an interval $ I $ if its solutions are oscillating (at $ + \infty $, respectively, on $ I $).
Among equations which are oscillatory at $ + \infty $ the equations which possess the properties $ A $ or $ B $, i.e. which are compatible in a specific sense with one of the equations
$$ u ^ {(} n) = - u \ \textrm{ or } \ u ^ {(} n) = u , $$
are distinguished. Equation (1) is said to possess property $ A $ if all its solutions defined in a neighbourhood of $ + \infty $ are oscillating when $ n $ is even; when $ n $ is odd, they should either be oscillating or satisfy the condition
$$ \tag{2 } \lim\limits _ {t \rightarrow + \infty } u ^ {(} i- 1) ( t) = 0,\ i = 1 \dots n. $$
If every solution of equation (1) defined in a neighbourhood of $ + \infty $, when $ n $ is even, is either oscillating, or satisfies condition (2) or
$$ \tag{3 } \lim\limits _ {t \rightarrow + \infty } | u ^ {(} i- 1) ( t) | = + \infty ,\ \ i = 1 \dots n, $$
while when $ n $ is odd, it is either oscillating or satisfies condition (3), then the equation possesses property $ B $.
The linear equation
$$ \tag{4 } u ^ {(} n) = a( t) u $$
with a locally summable coefficient $ a: [ t _ {0} , + \infty ) \rightarrow \mathbf R $ possesses property $ A $( property $ B $) if
$$ a( t) \leq 0 \ ( a( t) \geq 0) \ \textrm{ when } t \geq t _ {0} $$
and either
$$ \int\limits _ {t _ {0} } ^ { {+ } \infty } t ^ {n- 1- \epsilon } | a( t) | dt = + \infty $$
or
$$ a( t) \leq \frac{\mu _ {n} - \epsilon }{t ^ {n} } \ \left ( a( t) \geq \frac{\nu _ {n} + \epsilon }{t ^ {n} } \right ) $$
when $ t \geq t _ {0} $, where $ \epsilon > 0 $ and $ \mu _ {n} $ is the smallest ( $ \nu _ {n} $ is the largest) of the local minima (maxima) of the polynomial $ x( x- 1) \dots ( x- n+ 1) $( see [1]–[5]).
An equation of Emden–Fowler type
$$ \tag{5 } u ^ {(} n) = a( t) | u | ^ \lambda \mathop{\rm sign} u ,\ \ \lambda > 0,\ \lambda \neq 1, $$
with a locally summable non-positive (non-negative) coefficient $ a: [ t _ {0} , + \infty ) \rightarrow \mathbf R $ possesses property $ A $( property $ B $) if and only if
$$ \int\limits _ {t _ {0} } ^ { {+ } \infty } t ^ \mu | a( t) | dt = + \infty , $$
where $ \mu = \min \{ n- 1, ( n- 1) \lambda \} $( see [4], [6], [7]).
In a number of cases the question of the oscillation of equation (1) can be reduced to the same question for the standard equations of the form (4) and (5) using a comparison theorem (see [11]).
In studying the oscillatory properties of equations with deviating argument, certain specific features arise. For example, if $ n $ is odd, $ \Delta > 0 $, and if for large $ t $ the inequality
$$ a( t) \leq a _ {0} < - n! \Delta ^ {-} n $$
is fulfilled, then all non-zero solutions of the equation
$$ u ^ {(} n) ( t) = a( t) u( t - \Delta ) $$
are oscillatory at $ + \infty $( see [10], [11]). At the same time, if $ a $ is non-positive and $ n $ is odd, the non-retarded equation (4) always has a non-oscillating solution.
The concepts of oscillation and non-oscillation on an interval are generally studied for linear homogeneous equations. They are of fundamental value in the theory of boundary value problems (see [12]).
References
| [1] | A. Kneser, "Untersuchungen über die reellen Nullstellen der Integrale linearer Integralgleichungen" Math. Ann. , 42 (1893) pp. 409–435 |
| [2] | J.G. Mikusinksi, "On Fite's oscillation theorems" Colloq. Math. , 2 (1951) pp. 34–39 |
| [3] | V.A. Kondrat'ev, "The oscillatory character of solutions of the equation 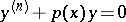 " Trudy Moskov. Mat. Obshch. , 10 (1961) pp. 419–436 (In Russian) " Trudy Moskov. Mat. Obshch. , 10 (1961) pp. 419–436 (In Russian) |
| [4] | I.T. Kiguradze, "On the oscillatory character of solutions of the equation 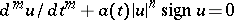 " Mat. Sb. , 65 : 2 (1964) pp. 172–187 (In Russian) " Mat. Sb. , 65 : 2 (1964) pp. 172–187 (In Russian) |
| [5] | T.A. Chanturiya, "On a comparison theorem for linear differential equations" Math. USSR Izv. , 10 : 5 (1976) pp. 1075–1088 Izv. Akad. Nauk. SSSR Ser. Mat. , 40 : 5 (1976) pp. 1128–1142 |
| [6] | I. Ličko, M. Švec, "La charactère oscillatoire des solutions de l'équation  , , 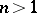 " Chekhosl. Mat. Zh. , 13 (1963) pp. 481–491 " Chekhosl. Mat. Zh. , 13 (1963) pp. 481–491 |
| [7] | I.T. Kiguradze, "On the oscillatory and monotone solutions of ordinary differential equations" Arch. Math. , 14 : 1 (1978) pp. 21–44 |
| [8] | C.A. Swanson, "Comparison and oscillation theory of linear differential equations" , Acad. Press (1968) |
| [9] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) |
| [10] | A.D. Myshkis, "Linear differential equations with retarded argument" , Moscow (1972) (In Russian) |
| [11] | R.G. Koplatadze, T.A. Chanturiya, "On the oscillatory properties of differential equations with deviating argument" , Tbilisi (1977) (In Russian) |
| [12] | A.Yu. Levin, "Non-oscillation of the solutions of the equation 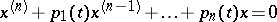 " Russian Math. Surveys , 24 : 2 (1969) pp. 43–99 Uspekhi Mat. Nauk , 24 : 2 (1969) pp. 43–96 " Russian Math. Surveys , 24 : 2 (1969) pp. 43–99 Uspekhi Mat. Nauk , 24 : 2 (1969) pp. 43–96 |
Comments
References
| [a1] | J.K. Hale, "Ordinary differential equations" , Wiley (1969) |
| [a2] | W.T. Reid, "Sturmian theory for ordinary differential equations" , Springer (1980) |
Oscillating differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Oscillating_differential_equation&oldid=12302