Difference between revisions of "Modules, category of"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | m0644801.png | ||
| + | $#A+1 = 35 n = 1 | ||
| + | $#C+1 = 35 : ~/encyclopedia/old_files/data/M064/M.0604480 Modules, category of | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | The | + | The [[Category|category]] mod- $ R $ |
| + | whose objects are the right unitary modules over an arbitrary associative ring $ R $ | ||
| + | with identity, and whose morphisms are the homomorphisms of $ R $- | ||
| + | modules. This category is the most important example of an [[Abelian category|Abelian category]]. Moreover, for every small Abelian category there is a full exact imbedding into some category of modules. | ||
| − | + | If $ R = \mathbf Z $, | |
| + | the ring of integers, then mod- $ R $ | ||
| + | is the category of Abelian groups, and if $ R = D $ | ||
| + | is a skew-field, then mod- $ R $ | ||
| + | is the category of vector spaces over $ D $. | ||
| − | + | The properties of mod- $ R $ | |
| + | reflect a number of important properties of the ring $ R $( | ||
| + | see [[Homological classification of rings|Homological classification of rings]]). Connected with this category is a number of important homological invariants of the ring; in particular, its [[Homological dimension|homological dimension]]. The centre of mod- $ R $( | ||
| + | that is, the set of natural transformations of the identity functor of the category) is isomorphic to the centre of $ R $. | ||
| − | the | + | In ring theory, homological algebra and algebraic $ K $- |
| + | theory, various subcategories of the category of modules are discussed; in particular, the subcategory of finitely-generated projective $ R $- | ||
| + | modules and the associated $ K $- | ||
| + | functors (see [[Algebraic K-theory|Algebraic $ K $- | ||
| + | theory]]). By analogy with [[Pontryagin duality|Pontryagin duality]], dualities between full subcategories of the category of modules have been studied; in particular between subcategories of finitely-generated modules. For example, it has been established that if $ R $ | ||
| + | and $ S $ | ||
| + | are Noetherian rings and if there is duality between finitely-generated right $ R $- | ||
| + | modules and finitely-generated left $ S $- | ||
| + | modules, then there is a bimodule $ {} _ {S} U _ {R} $ | ||
| + | such that the given duality is equivalent to the duality defined by the functors | ||
| − | + | $$ | |
| + | \mathop{\rm Hom} _ {R} ( - , U ) \ \ | ||
| + | \textrm{ and } \ \ | ||
| + | \mathop{\rm Hom} _ {S} ( - , U ) , | ||
| + | $$ | ||
| − | + | the ring of endomorphisms $ \mathop{\rm End} U _ {R} $ | |
| + | is isomorphic to $ S $, | ||
| + | $ \mathop{\rm End} {} _ {S} U $ | ||
| + | is isomorphic to $ R $, | ||
| + | the bimodule $ U $ | ||
| + | is a finitely-generated injective cogenerator (both as an $ R $- | ||
| + | module and an $ S $- | ||
| + | module), and the ring $ R $ | ||
| + | is semi-perfect (cf. [[Semi-perfect ring|Semi-perfect ring]]). The most important class of rings, arising in the consideration of duality of modules, is the class of quasi-Frobenius rings (cf. [[Quasi-Frobenius ring|Quasi-Frobenius ring]]). A left [[Artinian ring|Artinian ring]] $ R $ | ||
| + | is quasi-Frobenius if and only if the mapping | ||
| − | + | $$ | |
| − | + | M \rightarrow \mathop{\rm Hom} _ {R} ( M , R ) | |
| + | $$ | ||
| + | defines a duality between the categories of finitely-generated left and right $ R $- | ||
| + | modules. | ||
| + | ====References==== | ||
| + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Bass, "Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064480/m06448036.png" />-theory" , Benjamin (1968) {{MR|249491}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I. Bucur, A. Deleanu, "Introduction to the theory of categories and functors" , Wiley (1968) {{MR|0236236}} {{ZBL|0197.29205}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> C. Faith, "Algebra: rings, modules and categories" , '''1–2''' , Springer (1973–1976) {{MR|0551052}} {{MR|0491784}} {{MR|0366960}} {{ZBL|0508.16001}} {{ZBL|0266.16001}} </TD></TR></table> | ||
====Comments==== | ====Comments==== | ||
| − | A duality given by a bimodule | + | A duality given by a bimodule $ U $ |
| + | as described above is called a $ U $- | ||
| + | duality or Morita duality; cf. also (the comments to) [[Morita equivalence|Morita equivalence]]. | ||
Latest revision as of 08:01, 6 June 2020
The category mod- $ R $
whose objects are the right unitary modules over an arbitrary associative ring $ R $
with identity, and whose morphisms are the homomorphisms of $ R $-
modules. This category is the most important example of an Abelian category. Moreover, for every small Abelian category there is a full exact imbedding into some category of modules.
If $ R = \mathbf Z $, the ring of integers, then mod- $ R $ is the category of Abelian groups, and if $ R = D $ is a skew-field, then mod- $ R $ is the category of vector spaces over $ D $.
The properties of mod- $ R $ reflect a number of important properties of the ring $ R $( see Homological classification of rings). Connected with this category is a number of important homological invariants of the ring; in particular, its homological dimension. The centre of mod- $ R $( that is, the set of natural transformations of the identity functor of the category) is isomorphic to the centre of $ R $.
In ring theory, homological algebra and algebraic $ K $- theory, various subcategories of the category of modules are discussed; in particular, the subcategory of finitely-generated projective $ R $- modules and the associated $ K $- functors (see Algebraic $ K $- theory). By analogy with Pontryagin duality, dualities between full subcategories of the category of modules have been studied; in particular between subcategories of finitely-generated modules. For example, it has been established that if $ R $ and $ S $ are Noetherian rings and if there is duality between finitely-generated right $ R $- modules and finitely-generated left $ S $- modules, then there is a bimodule $ {} _ {S} U _ {R} $ such that the given duality is equivalent to the duality defined by the functors
$$ \mathop{\rm Hom} _ {R} ( - , U ) \ \ \textrm{ and } \ \ \mathop{\rm Hom} _ {S} ( - , U ) , $$
the ring of endomorphisms $ \mathop{\rm End} U _ {R} $ is isomorphic to $ S $, $ \mathop{\rm End} {} _ {S} U $ is isomorphic to $ R $, the bimodule $ U $ is a finitely-generated injective cogenerator (both as an $ R $- module and an $ S $- module), and the ring $ R $ is semi-perfect (cf. Semi-perfect ring). The most important class of rings, arising in the consideration of duality of modules, is the class of quasi-Frobenius rings (cf. Quasi-Frobenius ring). A left Artinian ring $ R $ is quasi-Frobenius if and only if the mapping
$$ M \rightarrow \mathop{\rm Hom} _ {R} ( M , R ) $$
defines a duality between the categories of finitely-generated left and right $ R $- modules.
References
| [1] | H. Bass, "Algebraic 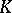 -theory" , Benjamin (1968) MR249491 -theory" , Benjamin (1968) MR249491 |
| [2] | I. Bucur, A. Deleanu, "Introduction to the theory of categories and functors" , Wiley (1968) MR0236236 Zbl 0197.29205 |
| [3] | C. Faith, "Algebra: rings, modules and categories" , 1–2 , Springer (1973–1976) MR0551052 MR0491784 MR0366960 Zbl 0508.16001 Zbl 0266.16001 |
Comments
A duality given by a bimodule $ U $ as described above is called a $ U $- duality or Morita duality; cf. also (the comments to) Morita equivalence.
Modules, category of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Modules,_category_of&oldid=17739