Difference between revisions of "Kähler manifold"
Ulf Rehmann (talk | contribs) m (moved Kaehler manifold to Kähler manifold over redirect: accented title) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | k0550701.png | ||
| + | $#A+1 = 76 n = 4 | ||
| + | $#C+1 = 76 : ~/encyclopedia/old_files/data/K055/K.0505070 K\AGahler manifold | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A [[Complex manifold|complex manifold]] which admits a [[Kähler metric|Kähler metric]]. Sometimes it is called a manifold of Kähler type, with the term "Kähler manifold" being reserved for manifolds actually equipped with a Kähler metric [[#References|[1]]]. Any submanifold of a Kähler manifold is a Kähler manifold. In particular, all projective complex algebraic varieties without singular points are Kähler manifolds, and, moreover, their Kähler metric is induced by the [[Fubini–Study metric|Fubini–Study metric]] on the complex projective space. Similarly, every submanifold in the affine space $ \mathbf C ^ {n} $( | |
| + | in particular, every [[Stein manifold|Stein manifold]]) is a Kähler manifold. Other examples of Kähler manifolds are obtained if one considers the quotient space $ M/ \Gamma $ | ||
| + | of a Kähler manifold $ M $ | ||
| + | by a discrete group $ \Gamma $ | ||
| + | of analytic automorphisms preserving the Kähler metric. In particular, every [[Complex torus|complex torus]] is a Kähler manifold. Any one-dimensional complex manifold is Kählerian. | ||
| − | + | The theory of harmonic forms on a compact Kähler manifold $ M $ | |
| + | yields the following properties of the de Rham and Dolbeault cohomology groups on $ M $( | ||
| + | see [[#References|[1]]], [[#References|[2]]], and also [[#References|[5]]], where these properties were first established for projective algebraic varieties): | ||
| − | + | $$ | |
| + | H ^ {r} ( M, \mathbf C ) \cong \ | ||
| + | \oplus \sum _ {p + q = r } | ||
| + | H ^ {p, q } ( M), | ||
| + | $$ | ||
| − | + | $$ | |
| + | H ^ {p, q } ( M) \cong H ^ {q, p } ( M), | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | \mathop{\rm dim} H ^ {2r + 1 } ( M, \mathbf C ) \ \textrm{ is } \textrm{ even } , | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | H ^ {2r} ( M, \mathbf C ) \neq 0 \ \textrm{ if } r | ||
| + | = 1 \dots { | ||
| + | \frac{1}{2} | ||
| + | } \mathop{\rm dim} _ {\mathbf C } M. | ||
| + | $$ | ||
Holomorphic forms on a compact Kähler manifold are closed. In particular, | Holomorphic forms on a compact Kähler manifold are closed. In particular, | ||
| − | + | $$ | |
| + | H ^ {1} ( M, \mathbf C ) \cong \ | ||
| + | A ^ {1} \oplus \overline{A}\; {} ^ {1} , | ||
| + | $$ | ||
| − | where | + | where $ A ^ {1} $ |
| + | is the space of all holomorphic $ 1 $- | ||
| + | forms on $ M $. | ||
| + | If $ \mathop{\rm dim} _ {\mathbf C } M = 1 $, | ||
| + | the number | ||
| − | + | $$ | |
| + | \mathop{\rm dim} A ^ {1} = \ | ||
| + | { | ||
| + | \frac{1}{2} | ||
| + | } \mathop{\rm dim} H ^ {1} ( M, \mathbf C ) | ||
| + | $$ | ||
| − | is the genus of | + | is the genus of $ M $ |
| + | as a compact Riemann surface (cf. also [[Genus of a surface|Genus of a surface]]; [[Riemann surface|Riemann surface]]). The above properties provide the basis for the construction of examples of non-Kähler compact manifolds, the simplest of which is the Hopf surface, which is diffeomorphic to $ S ^ {1} \times S ^ {3} $. | ||
| − | A Kähler manifold | + | A Kähler manifold $ M $ |
| + | is called a [[Hodge variety|Hodge variety]] if its Kähler metric is a Hodge metric. Any projective algebraic variety without singular points is a Hodge variety relative to the metric induced by the Fubini–Study metric. Conversely, any compact complex manifold $ M $ | ||
| + | equipped with a Kählerian Hodge metric $ \eta $ | ||
| + | can be biholomorphically imbedded in a complex projective space in such a way that the metric induced on $ M $ | ||
| + | by the Fubini–Study metric may be expressed as $ k \eta $ | ||
| + | for some natural number $ k $( | ||
| + | Kodaira's projective imbedding theorem [[#References|[1]]], [[#References|[3]]]). Thus, a compact complex manifold $ M $ | ||
| + | is isomorphic to a projective algebraic variety if and only if it is a Hodge variety. Another form of this criterion: A compact complex manifold $ M $ | ||
| + | is a projective algebraic variety if and only if it admits a [[Negative vector bundle|negative vector bundle]]. Kodaira's theorem can be generalized to complex spaces (see [[#References|[4]]], [[#References|[6]]]). Compact Kähler manifolds which are not Hodge varieties may be found among the two-dimensional complex tori. For example, this is the case for the torus $ \mathbf C ^ {2} / \Gamma $, | ||
| + | where $ \Gamma $ | ||
| + | is the lattice spanned by the vectors $ ( 1, 0) $, | ||
| + | $ ( 0, 1) $, | ||
| + | $ ( \sqrt - 2 , \sqrt - 3 ) $, | ||
| + | $ ( \sqrt - 5 , \sqrt - 7 ) $( | ||
| + | see [[#References|[1]]], [[#References|[3]]]). Another necessary and sufficient condition for an $ n $- | ||
| + | dimensional compact Kähler manifold $ M $ | ||
| + | to be projective is that there exist $ n $ | ||
| + | algebraically independent meromorphic functions on $ M $[[#References|[8]]]. | ||
Any non-compact complete Kähler manifold with positive [[Sectional curvature|sectional curvature]] is a [[Stein manifold|Stein manifold]]. The same is true of any simply-connected complete Kähler manifold of non-positive sectional curvature [[#References|[7]]]. | Any non-compact complete Kähler manifold with positive [[Sectional curvature|sectional curvature]] is a [[Stein manifold|Stein manifold]]. The same is true of any simply-connected complete Kähler manifold of non-positive sectional curvature [[#References|[7]]]. | ||
| Line 27: | Line 88: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Weil, "Introduction à l'Aeetude des variétés kahlériennes" , Hermann (1958)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.S. Chern, "Complex manifolds without potential theory" , Springer (1979)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> W.V.D. Hodge, "The theory and application of harmonic integrals" , Cambridge Univ. Press (1952)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> H. Grauert, "Ueber Modifikationen und exzeptionelle analytische Mengen" ''Math. Ann.'' , '''146''' (1962) pp. 331–368</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> R.E. Greene, H. Wu, "A theorem in complex geometric function theory" , ''Value-distribution Theory'' , '''A''' , M. Dekker (1974) pp. 145–167</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> B.G. Moishezon, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055070/k05507037.png" />-dimensional compact complex manifolds possessing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055070/k05507038.png" /> algebraically independent meromorphic functions I - III" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''30''' (1966) pp. 133–174; 345–386; 621–656 (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Weil, "Introduction à l'Aeetude des variétés kahlériennes" , Hermann (1958)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.S. Chern, "Complex manifolds without potential theory" , Springer (1979)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> W.V.D. Hodge, "The theory and application of harmonic integrals" , Cambridge Univ. Press (1952)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> H. Grauert, "Ueber Modifikationen und exzeptionelle analytische Mengen" ''Math. Ann.'' , '''146''' (1962) pp. 331–368</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> R.E. Greene, H. Wu, "A theorem in complex geometric function theory" , ''Value-distribution Theory'' , '''A''' , M. Dekker (1974) pp. 145–167</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> B.G. Moishezon, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055070/k05507037.png" />-dimensional compact complex manifolds possessing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055070/k05507038.png" /> algebraically independent meromorphic functions I - III" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''30''' (1966) pp. 133–174; 345–386; 621–656 (In Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
A complex compact surface is Kähler if and only if its first [[Betti number|Betti number]] is even. | A complex compact surface is Kähler if and only if its first [[Betti number|Betti number]] is even. | ||
| − | Let | + | Let $ M $ |
| + | be complex compact manifold of (complex) dimension $ m $. | ||
| + | Let $ g $ | ||
| + | be a Kähler metric on $ M $ | ||
| + | and $ \omega $ | ||
| + | its associated $ ( 1, 1) $- | ||
| + | form. (If $ g = \sum g _ {\alpha \overline \beta \; } dz ^ \alpha \otimes d \overline{z}\; {} ^ \beta $ | ||
| + | in local coordinates, then $ \omega = \sum g _ {\alpha \overline \beta \; } dz ^ \alpha \wedge d \overline{z}\; {} ^ \beta $; | ||
| + | giving $ \omega $ | ||
| + | amounts to the same thing as giving $ g $.) | ||
| + | Denote by $ \mathop{\rm Ric} _ {g} $ | ||
| + | the Ricci curvature tensor of $ ( M , g) $ | ||
| + | and let $ \gamma _ \omega $ | ||
| + | be the associated $ ( 1, 1) $ | ||
| + | form to $ \mathop{\rm Ric} _ {g} $. | ||
| + | Then, [[#References|[a1]]], the cohomology class of $ \gamma _ \omega $ | ||
| + | is $ 2 \pi $ | ||
| + | times the first Chern class of $ M $: | ||
| + | $ [ \gamma _ \omega ] = 2 \pi c _ {1} ( M) $. | ||
| − | Now let | + | Now let $ \widetilde \gamma $ |
| + | be a given $ ( 1, 1) $ | ||
| + | form on $ ( M, \omega ) $ | ||
| + | such that $ [ \gamma _ \omega ] = 2 \pi c _ {1} ( M) $. | ||
| + | Then the Calabi conjecture [[#References|[a2]]], [[#References|[a3]]] states that there is precisely one Kähler form $ \widetilde \omega $ | ||
| + | in the same class as $ \omega $ | ||
| + | such that $ \widetilde \gamma = \gamma _ {\widetilde \omega } $. | ||
| + | E. Calabi proved uniqueness. | ||
| − | A related conjecture is: Let | + | A related conjecture is: Let $ M $ |
| + | be a complex compact manifold which admits a negative first Chern form. Then there exists a unique Kähler form $ \omega $ | ||
| + | such that $ \gamma _ \omega = - \omega $. | ||
| − | Such a metric is called an Einstein–Kähler metric. (A Riemannian metric | + | Such a metric is called an Einstein–Kähler metric. (A Riemannian metric $ g $ |
| + | is called an Einstein metric if $ \mathop{\rm Ric} _ {g} = kg $ | ||
| + | for some constant $ k $.) | ||
The Calabi conjecture (existence) was proved by S.T. Yau [[#References|[a4]]], [[#References|[a5]]] and the second conjecture was proved by both T. Aubin and Yau, [[#References|[a5]]], [[#References|[a6]]]. | The Calabi conjecture (existence) was proved by S.T. Yau [[#References|[a4]]], [[#References|[a5]]] and the second conjecture was proved by both T. Aubin and Yau, [[#References|[a5]]], [[#References|[a6]]]. | ||
| − | A Kähler manifold is called a Calabi–Yau manifold if its first Chern class vanishes (so that there exists a Ricci flat on | + | A Kähler manifold is called a Calabi–Yau manifold if its first Chern class vanishes (so that there exists a Ricci flat on $ M $). |
| − | These manifolds are of great current interest in theoretical physics as prime candidates for the "missing six dimensions" for a | + | These manifolds are of great current interest in theoretical physics as prime candidates for the "missing six dimensions" for a $ 10 $- |
| + | dimensional super-string theory; i.e. the carrier space of this $ 10 $- | ||
| + | dimensional space would be $ M ^ {4} \times K $, | ||
| + | where $ M ^ {4} $ | ||
| + | is four-dimensional Minkowski space and $ K $ | ||
| + | is a six-dimensional ( "small" ) compact Calabi–Yau manifold. | ||
| − | The Calabi–Yau manifolds (with non-vanishing Euler number ( | + | The Calabi–Yau manifolds (with non-vanishing Euler number ( $ = $[[ |
| + | Euler characteristic|Euler characteristic]])) provide the only known "compactifications" $ M ^ {4} \times K $ | ||
| + | consistent with the super-string equations of motion. A selection of references dealing with these matters is [[#References|[a8]]]–[[#References|[a12]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S.S. Chern, "Characteristic classes of Hermitian manifolds" ''Ann. of Math.'' , '''47''' (1946) pp. 85–121</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> E. Calabi, "The space of Kähler metrics" , ''Proc. Internat. Congress Mathematicians (Amsterdam, 1954)'' , '''2''' , Noordhoff (1954) pp. 206–207</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> E. Calabi, "On Kähler manifolds with vanishing canonical class" R.H. Fox (ed.) D.C. Spencer (ed.) A.W. Tucker (ed.) , ''Algebraic geometry and topology (Symp. in honor of S. Lefschetz)'' , Princeton Univ. Press (1955) pp. 78–89</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> S.-T. Yau, "On Calabi's conjecture and some new results in algebraic geometry" ''Proc. Nat. Acad. Sci. USA'' , '''74''' (1977) pp. 1798–1799</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> S.-T. Yau, "On the Ricci curvature of a compact Kähler manifold and the complex Monge–Ampère equation I" ''Comm. Pure Appl. Math.'' , '''31''' (1978) pp. 339–411</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> T. Aubin, "Equations du type de Monge–Ampère sur les variétés kähleriennes compactes" ''C.R. Acad. Sci. Paris'' , '''283''' (1976) pp. 119–121</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> J.-P. Bourguignon, "Premières formes de Chern des variétés kähleriennes compactes" , ''Sem. Bourbaki 1977/1978'' , '''Exp. 507''' , Springer (1979) pp. 1–21</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> T. Huebsch, "Calabi–Yau manifolds—motivations and constructions" ''Comm. Math. Phys.'' , '''108''' (1987) pp. 291–318</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> M.B. Green, J.H. Schwarz, E. Witten, "Superstring theory" , '''2. Loop amplitudes, anomalies & phenomenology''' , Cambridge Univ. Press (1987) pp. 438ff</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> P. Candelas, G. Horowitz, A. Strominger, E. Witten, "Vacuum configurations for superstrings" ''Nuclear Physics'' , '''B258''' (1958) pp. 46–74</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> B. de Wit, D.J. Smit, N.D. Hari-Dass, "Residual supersymmetry of compactified <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055070/k05507079.png" /> supergravity" ''Nuclear Physics'' , '''B283''' (1987) pp. 165–191</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> D. Gepner, "Exactly solvable string compactifications on manifolds of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055070/k05507080.png" /> holonomy" ''Physics Letters'' , '''B199''' (1987) pp. 380–388</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> "Première classe de Chern et courbure de Ricci: preuve de la conjecture de Calabi" , ''Sem. Palaiseau 1978'' , Soc. Math. France (1978)</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> Y.-T. Siu, "Lectures on Hermitean–Einstein metrics for stable bundles and Kähler–Einstein metrics" , Birkhäuser (1987)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S.S. Chern, "Characteristic classes of Hermitian manifolds" ''Ann. of Math.'' , '''47''' (1946) pp. 85–121</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> E. Calabi, "The space of Kähler metrics" , ''Proc. Internat. Congress Mathematicians (Amsterdam, 1954)'' , '''2''' , Noordhoff (1954) pp. 206–207</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> E. Calabi, "On Kähler manifolds with vanishing canonical class" R.H. Fox (ed.) D.C. Spencer (ed.) A.W. Tucker (ed.) , ''Algebraic geometry and topology (Symp. in honor of S. Lefschetz)'' , Princeton Univ. Press (1955) pp. 78–89</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> S.-T. Yau, "On Calabi's conjecture and some new results in algebraic geometry" ''Proc. Nat. Acad. Sci. USA'' , '''74''' (1977) pp. 1798–1799</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> S.-T. Yau, "On the Ricci curvature of a compact Kähler manifold and the complex Monge–Ampère equation I" ''Comm. Pure Appl. Math.'' , '''31''' (1978) pp. 339–411</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> T. Aubin, "Equations du type de Monge–Ampère sur les variétés kähleriennes compactes" ''C.R. Acad. Sci. Paris'' , '''283''' (1976) pp. 119–121</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> J.-P. Bourguignon, "Premières formes de Chern des variétés kähleriennes compactes" , ''Sem. Bourbaki 1977/1978'' , '''Exp. 507''' , Springer (1979) pp. 1–21</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> T. Huebsch, "Calabi–Yau manifolds—motivations and constructions" ''Comm. Math. Phys.'' , '''108''' (1987) pp. 291–318</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> M.B. Green, J.H. Schwarz, E. Witten, "Superstring theory" , '''2. Loop amplitudes, anomalies & phenomenology''' , Cambridge Univ. Press (1987) pp. 438ff</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> P. Candelas, G. Horowitz, A. Strominger, E. Witten, "Vacuum configurations for superstrings" ''Nuclear Physics'' , '''B258''' (1958) pp. 46–74</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> B. de Wit, D.J. Smit, N.D. Hari-Dass, "Residual supersymmetry of compactified <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055070/k05507079.png" /> supergravity" ''Nuclear Physics'' , '''B283''' (1987) pp. 165–191</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> D. Gepner, "Exactly solvable string compactifications on manifolds of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055070/k05507080.png" /> holonomy" ''Physics Letters'' , '''B199''' (1987) pp. 380–388</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> "Première classe de Chern et courbure de Ricci: preuve de la conjecture de Calabi" , ''Sem. Palaiseau 1978'' , Soc. Math. France (1978)</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> Y.-T. Siu, "Lectures on Hermitean–Einstein metrics for stable bundles and Kähler–Einstein metrics" , Birkhäuser (1987)</TD></TR></table> | ||
Revision as of 22:15, 5 June 2020
A complex manifold which admits a Kähler metric. Sometimes it is called a manifold of Kähler type, with the term "Kähler manifold" being reserved for manifolds actually equipped with a Kähler metric [1]. Any submanifold of a Kähler manifold is a Kähler manifold. In particular, all projective complex algebraic varieties without singular points are Kähler manifolds, and, moreover, their Kähler metric is induced by the Fubini–Study metric on the complex projective space. Similarly, every submanifold in the affine space $ \mathbf C ^ {n} $(
in particular, every Stein manifold) is a Kähler manifold. Other examples of Kähler manifolds are obtained if one considers the quotient space $ M/ \Gamma $
of a Kähler manifold $ M $
by a discrete group $ \Gamma $
of analytic automorphisms preserving the Kähler metric. In particular, every complex torus is a Kähler manifold. Any one-dimensional complex manifold is Kählerian.
The theory of harmonic forms on a compact Kähler manifold $ M $ yields the following properties of the de Rham and Dolbeault cohomology groups on $ M $( see [1], [2], and also [5], where these properties were first established for projective algebraic varieties):
$$ H ^ {r} ( M, \mathbf C ) \cong \ \oplus \sum _ {p + q = r } H ^ {p, q } ( M), $$
$$ H ^ {p, q } ( M) \cong H ^ {q, p } ( M), $$
$$ \mathop{\rm dim} H ^ {2r + 1 } ( M, \mathbf C ) \ \textrm{ is } \textrm{ even } , $$
$$ H ^ {2r} ( M, \mathbf C ) \neq 0 \ \textrm{ if } r = 1 \dots { \frac{1}{2} } \mathop{\rm dim} _ {\mathbf C } M. $$
Holomorphic forms on a compact Kähler manifold are closed. In particular,
$$ H ^ {1} ( M, \mathbf C ) \cong \ A ^ {1} \oplus \overline{A}\; {} ^ {1} , $$
where $ A ^ {1} $ is the space of all holomorphic $ 1 $- forms on $ M $. If $ \mathop{\rm dim} _ {\mathbf C } M = 1 $, the number
$$ \mathop{\rm dim} A ^ {1} = \ { \frac{1}{2} } \mathop{\rm dim} H ^ {1} ( M, \mathbf C ) $$
is the genus of $ M $ as a compact Riemann surface (cf. also Genus of a surface; Riemann surface). The above properties provide the basis for the construction of examples of non-Kähler compact manifolds, the simplest of which is the Hopf surface, which is diffeomorphic to $ S ^ {1} \times S ^ {3} $.
A Kähler manifold $ M $ is called a Hodge variety if its Kähler metric is a Hodge metric. Any projective algebraic variety without singular points is a Hodge variety relative to the metric induced by the Fubini–Study metric. Conversely, any compact complex manifold $ M $ equipped with a Kählerian Hodge metric $ \eta $ can be biholomorphically imbedded in a complex projective space in such a way that the metric induced on $ M $ by the Fubini–Study metric may be expressed as $ k \eta $ for some natural number $ k $( Kodaira's projective imbedding theorem [1], [3]). Thus, a compact complex manifold $ M $ is isomorphic to a projective algebraic variety if and only if it is a Hodge variety. Another form of this criterion: A compact complex manifold $ M $ is a projective algebraic variety if and only if it admits a negative vector bundle. Kodaira's theorem can be generalized to complex spaces (see [4], [6]). Compact Kähler manifolds which are not Hodge varieties may be found among the two-dimensional complex tori. For example, this is the case for the torus $ \mathbf C ^ {2} / \Gamma $, where $ \Gamma $ is the lattice spanned by the vectors $ ( 1, 0) $, $ ( 0, 1) $, $ ( \sqrt - 2 , \sqrt - 3 ) $, $ ( \sqrt - 5 , \sqrt - 7 ) $( see [1], [3]). Another necessary and sufficient condition for an $ n $- dimensional compact Kähler manifold $ M $ to be projective is that there exist $ n $ algebraically independent meromorphic functions on $ M $[8].
Any non-compact complete Kähler manifold with positive sectional curvature is a Stein manifold. The same is true of any simply-connected complete Kähler manifold of non-positive sectional curvature [7].
References
| [1] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) |
| [2] | A. Weil, "Introduction à l'Aeetude des variétés kahlériennes" , Hermann (1958) |
| [3] | S.S. Chern, "Complex manifolds without potential theory" , Springer (1979) |
| [4] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) |
| [5] | W.V.D. Hodge, "The theory and application of harmonic integrals" , Cambridge Univ. Press (1952) |
| [6] | H. Grauert, "Ueber Modifikationen und exzeptionelle analytische Mengen" Math. Ann. , 146 (1962) pp. 331–368 |
| [7] | R.E. Greene, H. Wu, "A theorem in complex geometric function theory" , Value-distribution Theory , A , M. Dekker (1974) pp. 145–167 |
| [8] | B.G. Moishezon, "On  -dimensional compact complex manifolds possessing -dimensional compact complex manifolds possessing  algebraically independent meromorphic functions I - III" Izv. Akad. Nauk SSSR Ser. Mat. , 30 (1966) pp. 133–174; 345–386; 621–656 (In Russian) algebraically independent meromorphic functions I - III" Izv. Akad. Nauk SSSR Ser. Mat. , 30 (1966) pp. 133–174; 345–386; 621–656 (In Russian) |
Comments
A complex compact surface is Kähler if and only if its first Betti number is even.
Let $ M $ be complex compact manifold of (complex) dimension $ m $. Let $ g $ be a Kähler metric on $ M $ and $ \omega $ its associated $ ( 1, 1) $- form. (If $ g = \sum g _ {\alpha \overline \beta \; } dz ^ \alpha \otimes d \overline{z}\; {} ^ \beta $ in local coordinates, then $ \omega = \sum g _ {\alpha \overline \beta \; } dz ^ \alpha \wedge d \overline{z}\; {} ^ \beta $; giving $ \omega $ amounts to the same thing as giving $ g $.) Denote by $ \mathop{\rm Ric} _ {g} $ the Ricci curvature tensor of $ ( M , g) $ and let $ \gamma _ \omega $ be the associated $ ( 1, 1) $ form to $ \mathop{\rm Ric} _ {g} $. Then, [a1], the cohomology class of $ \gamma _ \omega $ is $ 2 \pi $ times the first Chern class of $ M $: $ [ \gamma _ \omega ] = 2 \pi c _ {1} ( M) $.
Now let $ \widetilde \gamma $ be a given $ ( 1, 1) $ form on $ ( M, \omega ) $ such that $ [ \gamma _ \omega ] = 2 \pi c _ {1} ( M) $. Then the Calabi conjecture [a2], [a3] states that there is precisely one Kähler form $ \widetilde \omega $ in the same class as $ \omega $ such that $ \widetilde \gamma = \gamma _ {\widetilde \omega } $. E. Calabi proved uniqueness.
A related conjecture is: Let $ M $ be a complex compact manifold which admits a negative first Chern form. Then there exists a unique Kähler form $ \omega $ such that $ \gamma _ \omega = - \omega $.
Such a metric is called an Einstein–Kähler metric. (A Riemannian metric $ g $ is called an Einstein metric if $ \mathop{\rm Ric} _ {g} = kg $ for some constant $ k $.)
The Calabi conjecture (existence) was proved by S.T. Yau [a4], [a5] and the second conjecture was proved by both T. Aubin and Yau, [a5], [a6].
A Kähler manifold is called a Calabi–Yau manifold if its first Chern class vanishes (so that there exists a Ricci flat on $ M $).
These manifolds are of great current interest in theoretical physics as prime candidates for the "missing six dimensions" for a $ 10 $- dimensional super-string theory; i.e. the carrier space of this $ 10 $- dimensional space would be $ M ^ {4} \times K $, where $ M ^ {4} $ is four-dimensional Minkowski space and $ K $ is a six-dimensional ( "small" ) compact Calabi–Yau manifold.
The Calabi–Yau manifolds (with non-vanishing Euler number ( $ = $[[ Euler characteristic|Euler characteristic]])) provide the only known "compactifications" $ M ^ {4} \times K $ consistent with the super-string equations of motion. A selection of references dealing with these matters is [a8]–[a12].
References
| [a1] | S.S. Chern, "Characteristic classes of Hermitian manifolds" Ann. of Math. , 47 (1946) pp. 85–121 |
| [a2] | E. Calabi, "The space of Kähler metrics" , Proc. Internat. Congress Mathematicians (Amsterdam, 1954) , 2 , Noordhoff (1954) pp. 206–207 |
| [a3] | E. Calabi, "On Kähler manifolds with vanishing canonical class" R.H. Fox (ed.) D.C. Spencer (ed.) A.W. Tucker (ed.) , Algebraic geometry and topology (Symp. in honor of S. Lefschetz) , Princeton Univ. Press (1955) pp. 78–89 |
| [a4] | S.-T. Yau, "On Calabi's conjecture and some new results in algebraic geometry" Proc. Nat. Acad. Sci. USA , 74 (1977) pp. 1798–1799 |
| [a5] | S.-T. Yau, "On the Ricci curvature of a compact Kähler manifold and the complex Monge–Ampère equation I" Comm. Pure Appl. Math. , 31 (1978) pp. 339–411 |
| [a6] | T. Aubin, "Equations du type de Monge–Ampère sur les variétés kähleriennes compactes" C.R. Acad. Sci. Paris , 283 (1976) pp. 119–121 |
| [a7] | J.-P. Bourguignon, "Premières formes de Chern des variétés kähleriennes compactes" , Sem. Bourbaki 1977/1978 , Exp. 507 , Springer (1979) pp. 1–21 |
| [a8] | T. Huebsch, "Calabi–Yau manifolds—motivations and constructions" Comm. Math. Phys. , 108 (1987) pp. 291–318 |
| [a9] | M.B. Green, J.H. Schwarz, E. Witten, "Superstring theory" , 2. Loop amplitudes, anomalies & phenomenology , Cambridge Univ. Press (1987) pp. 438ff |
| [a10] | P. Candelas, G. Horowitz, A. Strominger, E. Witten, "Vacuum configurations for superstrings" Nuclear Physics , B258 (1958) pp. 46–74 |
| [a11] | B. de Wit, D.J. Smit, N.D. Hari-Dass, "Residual supersymmetry of compactified 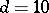 supergravity" Nuclear Physics , B283 (1987) pp. 165–191 supergravity" Nuclear Physics , B283 (1987) pp. 165–191 |
| [a12] | D. Gepner, "Exactly solvable string compactifications on manifolds of 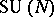 holonomy" Physics Letters , B199 (1987) pp. 380–388 holonomy" Physics Letters , B199 (1987) pp. 380–388 |
| [a13] | "Première classe de Chern et courbure de Ricci: preuve de la conjecture de Calabi" , Sem. Palaiseau 1978 , Soc. Math. France (1978) |
| [a14] | Y.-T. Siu, "Lectures on Hermitean–Einstein metrics for stable bundles and Kähler–Einstein metrics" , Birkhäuser (1987) |
Kähler manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=K%C3%A4hler_manifold&oldid=23350