Difference between revisions of "Hypercontractive semi-group"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | h1104001.png | ||
| + | $#A+1 = 85 n = 1 | ||
| + | $#C+1 = 85 : ~/encyclopedia/old_files/data/H110/H.1100400 Hypercontractive semi\AAhgroup | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A [[Semi-group|semi-group]] $ e ^ {- tH } $ | |
| + | of Hermitian operators (cf. also [[Semi-group of operators|Semi-group of operators]]) on a [[Hilbert space|Hilbert space]] $ L _ {2} ( X, \mu ) $ | ||
| + | such that: | ||
| − | + | 1) $ \| {e ^ {- tH } f } \| _ {L _ {p} } \leq \| f \| _ {L _ {p} } $ | |
| + | for all $ t > 0 $, | ||
| + | $ p \in [ 1, \infty ] $ | ||
| + | and $ f \in L _ {2} $; | ||
| − | + | 2) there exist $ T > 0 $ | |
| + | and $ b < \infty $ | ||
| + | such that $ \| {e ^ {- TH } f } \| _ {L _ {4} } \leq b \| f \| _ {L _ {2} } $ | ||
| + | for all $ f \in L _ {2} $. | ||
| + | Semi-groups having properties similar to 1) and 2) were first introduced by E. Nelson [[#References|[a9]]] to prove that the Hamiltonian operators arising in some models of [[Quantum field theory|quantum field theory]] are bounded below. In the important case that $ \mu ( X ) < \infty $, | ||
| + | condition 2) can be replaced by the following more natural condition, to which 2) is equivalent in the presence of 1): | ||
| − | + | 3) for every $ p,q \in ( 1, \infty ) $ | |
| + | there exists a $ t = t ( p,q ) $, | ||
| + | depending on $ p $ | ||
| + | and $ q $, | ||
| + | such that $ e ^ {- tH } $( | ||
| + | restricted or extended to $ L _ {p} $) | ||
| + | is a bounded operator from $ L _ {p} ( X, \mu ) $ | ||
| + | to $ L _ {q} ( X, \mu ) $. | ||
| + | Interpolation theorems are used in the proof. Below, all $ L _ {p} $ | ||
| + | spaces are taken to be real for simplicity and it is assumed that $ \mu ( X ) = 1 $, | ||
| + | this being the case of principal interest. | ||
| − | + | The prototypical example of a hypercontractive semi-group is given by choosing $ X = \mathbf R ^ {n} $ | |
| + | and | ||
| − | + | $$ | |
| + | d \mu ( x ) = ( 2 \pi ) ^ {- n/2 } e ^ {- { {\left | x \right | ^ {2} } / 2 } } dx. | ||
| + | $$ | ||
| − | ( | + | Denote by $ ( {\partial / {\partial x _ {j} } } ) ^ {*} $ |
| + | the adjoint of differentiation computed in $ L _ {2} ( \mathbf R ^ {n} , \mu ) $. | ||
| + | Let | ||
| − | + | $$ | |
| + | H = { | ||
| + | \frac{1}{2} | ||
| + | } \sum _ {j = 1 } ^ { n } \left ( { | ||
| + | \frac \partial {\partial x _ {j} } | ||
| + | } \right ) ^ {*} { | ||
| + | \frac \partial {\partial x _ {j} } | ||
| + | } . | ||
| + | $$ | ||
| − | + | (This should be interpreted as a closed version of the Ornstein–Uhlenbeck operator with $ C _ {c} ^ \infty $ | |
| + | as a core.) Then $ e ^ {- tH } $ | ||
| + | is a hypercontractive semi-group. In fact, $ b $ | ||
| + | can be taken equal to one in condition 2). Furthermore, for this semi-group the smallest time $ t $ | ||
| + | for boundedness in condition 3) is known. One has Nelson's family of hypercontractive inequalities: for $ 1 < p \leq q < \infty $, | ||
| − | + | $$ \tag{a1 } | |
| + | \left \| {e ^ {- tH } } \right \| _ {L _ {p} \rightarrow L _ {q} } \leq 1 \iff e ^ {- 2t } \leq { | ||
| + | \frac{( p - 1 ) }{( q - 1 ) } | ||
| + | } . | ||
| + | $$ | ||
| − | + | Moreover, $ \| {e ^ {- tH } } \| _ {L _ {p} \rightarrow L _ {q} } = \infty $ | |
| + | if $ e ^ {- 2t } > { {( p - 1 ) } / {( q - 1 ) } } $. | ||
| + | In (a1) one should regard the operators $ e ^ {- tH } $ | ||
| + | as restricted or extended to $ L _ {p} $. | ||
| − | + | If in (a1) one chooses $ p = 2 $ | |
| + | and $ q = q ( t ) = 1 + e ^ {2t } $, | ||
| + | then (a1) yields | ||
| − | + | $$ \tag{a2 } | |
| + | \left \| {e ^ {- tH } f } \right \| _ {L _ {q ( t ) } } \leq \left \| f \right \| _ {L _ {2} } \textrm{ for } t \geq 0, f \in L _ {2} ( \mathbf R ^ {n} , \mu ) . | ||
| + | $$ | ||
| − | + | This inequality becomes an equality for $ t = 0 $. | |
| + | Therefore it can be differentiated at $ t = 0 $ | ||
| + | for $ f $ | ||
| + | smooth enough. One gets the following logarithmic Sobolev inequality [[#References|[a7]]]: | ||
| − | + | $$ \tag{a3 } | |
| + | \int\limits _ {\mathbf R ^ {n} } {\left | {f ( x ) } \right | ^ {2} { \mathop{\rm ln} } \left | {f ( x ) } \right | } {d \mu ( x ) } \leq | ||
| + | $$ | ||
| − | + | $$ | |
| + | \leq | ||
| + | \int\limits _ {\mathbf R ^ {n} } {\left | { { \mathop{\rm grad} } f ( x ) } \right | ^ {2} } {d \mu ( x ) } + \left \| f \right \| _ {L _ {2} } ^ {2} { \mathop{\rm ln} } \left \| f \right \| _ {L _ {2} } . | ||
| + | $$ | ||
| − | + | Nelson's family of hypercontractive inequalities (a1) can be recovered easily from the single logarithmic Sobolev inequality (a3) [[#References|[a7]]]. More generally, L. Gross [[#References|[a7]]] established an equivalence between hypercontractivity conditions such as 1) and 2), on the one hand, and, on the other hand, coercivity inequalities for $ H $ | |
| + | of the form | ||
| − | ( | + | $$ \tag{a4 } |
| + | \int\limits _ { X } {\left | {f ( x ) } \right | ^ {2} { \mathop{\rm ln} } \left | {f ( x ) } \right | } {d \mu ( x ) } \leq | ||
| + | $$ | ||
| − | + | $$ | |
| + | \leq | ||
| + | c ( Hf,f ) + m \left \| f \right \| ^ {2} _ {L _ {2} } + \left \| f \right \| ^ {2} _ {L _ {2} } { \mathop{\rm ln} } \left \| f \right \| _ {L _ {2} } | ||
| + | $$ | ||
| − | + | (which reduces to (a3) in the previous example if one takes $ c = 1 $ | |
| + | and $ m = 0 $). | ||
| + | These coercivity inequalities have come to be known in general as logarithmic Sobolev inequalities. Because of this equivalence the theory of hypercontractive semi-groups has, to a great extent, been developed in conjunction with the theory of logarithmic Sobolev inequalities. The equivalence of (a4) with 1) and 2) is valid only for a class of operators $ H $ | ||
| + | which includes the important category of Dirichlet-form operators. See the survey [[#References|[a8]]] for further generality and for references to the early history of these two topics. | ||
| − | + | By way of application, if one can establish inequalities of the form (a4) for an elliptic partial [[Differential operator|differential operator]] $ H $ | |
| + | on a [[Riemannian manifold|Riemannian manifold]], then one half of the equivalence theorem shows that the semi-group $ e ^ {- tH } $ | ||
| + | has boundedness properties similar to 3), with a specifically given function $ t ( p,q ) $. | ||
| + | Since $ e ^ {- tH } $ | ||
| + | is an [[Integral operator|integral operator]], with kernel $ K _ {t} ( x,y ) $ | ||
| + | say, these norm bounds on $ e ^ {- tH } $ | ||
| + | can be converted into direct estimates on the size of the so-called "heat kernel" $ K _ {t} ( x,y ) $. | ||
| + | See [[#References|[a4]]] for a self-contained exposition of this method of obtaining pointwise heat kernel bounds for elliptic partial differential operators. | ||
| − | + | There are three basic consequences of the logarithmic Sobolev inequality (a4) which do not require $ H $ | |
| + | to be a Dirichlet-form operator but merely self-adjoint (cf. [[Self-adjoint operator|Self-adjoint operator]]). | ||
| − | + | i) The Federbush–Faris semi-boundedness theorem asserts that (a4) is equivalent to the condition that the (generally unbounded) operator $ H + V $ | |
| + | is in fact bounded below for all real-valued measurable functions $ V $ | ||
| + | on $ X $ | ||
| + | satisfying $ \| {e ^ {- V } } \| _ {L _ {2} ( \mu ) } < \infty $. | ||
| − | A very simple example of another semi-group satisfying Nelson's hypercontractivity inequalities (a1) is as follows. Denote by | + | ii) The Segal–Faris additivity theorem asserts that if $ H _ {1} $ |
| + | and $ H _ {2} $ | ||
| + | both satisfy (a4), then so does the independent sum $ H _ {1} \otimes I + I \otimes H _ {2} $. | ||
| + | |||
| + | iii) The Rothaus–Simon spectral gap theorem asserts that if (a4) holds with $ m = 0 $ | ||
| + | and if $ H1 = 0 $, | ||
| + | then $ H $ | ||
| + | has no spectrum (cf. [[Spectrum of an operator|Spectrum of an operator]]) in the interval $ ( 0,c ^ {- 1 } ) $. | ||
| + | For precise statements of these theorems and proofs see the survey [[#References|[a8]]]. | ||
| + | |||
| + | A very simple example of another semi-group satisfying Nelson's hypercontractivity inequalities (a1) is as follows. Denote by $ X $ | ||
| + | the two-point set $ \{ - 1,1 \} $. | ||
| + | Define $ \mu ( \{ - 1 \} ) = \mu ( \{ 1 \} ) = {1 / 2 } $. | ||
| + | Let $ H $ | ||
| + | be the projection onto the orthogonal complement of the constant functions in $ L _ {2} ( X, \mu ) $. | ||
| + | Then (a1) holds. Moreover, (a4) holds with $ c = 1 $ | ||
| + | and $ m = 0 $. | ||
| + | Since $ L _ {2} ( X, \mu ) $ | ||
| + | is two-dimensional, the proof of (a4) reduces in this example to a few lines of elementary calculus (see, e.g., [[#References|[a8]]], Example 2.6). The resulting inequality is known as the two-point logarithmic Sobolev inequality. Now, by the Segal–Faris additivity theorem there follows by induction a logarithmic Sobolev inequality on the product space $ \{ - 1,1 \} ^ {k} $ | ||
| + | for the product measure. An application of the [[Central limit theorem|central limit theorem]] then allows one to take the limit as $ k \rightarrow \infty $ | ||
| + | and arrive at the inequality (a3) (first for $ n = 1 $, | ||
| + | then, by additivity, for general $ n $). | ||
| + | This method of deriving the differential inequalities (a1) from discrete inequalities via the central limit theorem [[#References|[a3]]], [[#References|[a7]]] has also been used [[#References|[a2]]] to derive the sharp Hausdorff–Young inequality (cf. [[Hausdorff–Young inequalities|Hausdorff–Young inequalities]]) for the [[Fourier transform|Fourier transform]] on $ \mathbf R ^ {n} $. | ||
The notions of hypercontractivity and logarithmic Sobolev inequalities can also be formulated in the context of non-commutative integration theory, specifically over Clifford algebras (cf. [[Clifford algebra|Clifford algebra]]). See [[#References|[a8]]], Sect. 6(v), for a survey. | The notions of hypercontractivity and logarithmic Sobolev inequalities can also be formulated in the context of non-commutative integration theory, specifically over Clifford algebras (cf. [[Clifford algebra|Clifford algebra]]). See [[#References|[a8]]], Sect. 6(v), for a survey. | ||
| Line 55: | Line 161: | ||
Applications of both concepts to statistical mechanics are rapidly increasing at the present time (1996). For a survey of work through 1992, see [[#References|[a10]]]. For applications to the theory of large deviations, see [[#References|[a5]]]. For recent applications to statistics, see the survey [[#References|[a6]]]. | Applications of both concepts to statistical mechanics are rapidly increasing at the present time (1996). For a survey of work through 1992, see [[#References|[a10]]]. For applications to the theory of large deviations, see [[#References|[a5]]]. For recent applications to statistics, see the survey [[#References|[a6]]]. | ||
| − | Unlike the classical Sobolev inequalities, logarithmic Sobolev inequalities tend to be dimension independent and valid in many infinite-dimensional settings. For example, the inequality (a3) is meaningful and correct when | + | Unlike the classical Sobolev inequalities, logarithmic Sobolev inequalities tend to be dimension independent and valid in many infinite-dimensional settings. For example, the inequality (a3) is meaningful and correct when $ n = \infty $. |
| + | One need only interpret the first integrand on the right as | ||
| − | + | $$ | |
| + | \sum _ {k = 1 } ^ \infty \left | { { | ||
| + | \frac{\partial f }{\partial x _ {k} } | ||
| + | } } \right | ^ {2} . | ||
| + | $$ | ||
The dimension independence accounts, in part, for their usefulness in statistical mechanics (cf. also [[Statistical mechanics, mathematical problems in|Statistical mechanics, mathematical problems in]]), statistics, and large deviations, and for their origin in constructive [[Quantum field theory|quantum field theory]]. | The dimension independence accounts, in part, for their usefulness in statistical mechanics (cf. also [[Statistical mechanics, mathematical problems in|Statistical mechanics, mathematical problems in]]), statistics, and large deviations, and for their origin in constructive [[Quantum field theory|quantum field theory]]. | ||
| − | The survey [[#References|[a8]]] discusses the topics up through 1992. [[#References|[a1]]] also surveys related topics and describes various methods for proving logarithmic Sobolev inequalities for specific operators | + | The survey [[#References|[a8]]] discusses the topics up through 1992. [[#References|[a1]]] also surveys related topics and describes various methods for proving logarithmic Sobolev inequalities for specific operators $ H $. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Bakry, "L'hypercontractivité et son utilisation en théorie des semi-groups" P. Bernard (ed.) , ''Lectures on Probability Theory'' , ''Lecture Notes in Mathematics'' , '''1581''' , Springer (1994) pp. 1–114</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Beckner, "Inequalities in Fourier analysis" ''Ann. of Math.'' , '''102''' (1975) pp. 159–182</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Bonami, "Études des coefficients de Fourier des fonctions de <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110400/h11040086.png" />" ''Ann. Inst. Fourier'' , '''20''' : 2 (1970) pp. 335–402</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> E.B. Davies, "Heat kernels and spectral theory" , Cambridge Univ. Press (1989)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J. D. Deuschel, D. W. Stroock, "Large deviations" , ''Pure Appl. Math.'' , '''137''' , Acad. Press (1989)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P. Diaconis, L. Saloff-Coste, "Logarithmic Sobolev inequalities for finite Markov chains" ''Ann. Appl. Probab.'' (1996)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> L. Gross, "Logarithmic Sobolev inequalities" ''Amer. J. of Math.'' , '''97''' (1975) pp. 1061–1083</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> L. Gross, "Logarithmic Sobolev inequalities and contractivity properties of semigroups" G. Dell'Antonio (ed.) U. Mosco (ed.) , ''Dirichlet Forms'' , ''Lecture Notes in Mathematics'' , '''1563''' , Springer (1993) pp. 54–88</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> E. Nelson, "A quartic interaction in two dimensions" R. Goodman (ed.) I.E. Segal (ed.) , ''Mathematical Theory of Elementary Particles'' , MIT (1966) pp. 69–73</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> D. Stroock, "Logarithmic Sobolev inequalities for Gibbs states" G. Dell'Antonio (ed.) U. Mosco (ed.) , ''Dirichlet Forms'' , ''Lecture Notes in Mathematics'' , '''1563''' , Springer (1993) pp. 194–228</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Bakry, "L'hypercontractivité et son utilisation en théorie des semi-groups" P. Bernard (ed.) , ''Lectures on Probability Theory'' , ''Lecture Notes in Mathematics'' , '''1581''' , Springer (1994) pp. 1–114</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Beckner, "Inequalities in Fourier analysis" ''Ann. of Math.'' , '''102''' (1975) pp. 159–182</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Bonami, "Études des coefficients de Fourier des fonctions de <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110400/h11040086.png" />" ''Ann. Inst. Fourier'' , '''20''' : 2 (1970) pp. 335–402</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> E.B. Davies, "Heat kernels and spectral theory" , Cambridge Univ. Press (1989)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J. D. Deuschel, D. W. Stroock, "Large deviations" , ''Pure Appl. Math.'' , '''137''' , Acad. Press (1989)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P. Diaconis, L. Saloff-Coste, "Logarithmic Sobolev inequalities for finite Markov chains" ''Ann. Appl. Probab.'' (1996)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> L. Gross, "Logarithmic Sobolev inequalities" ''Amer. J. of Math.'' , '''97''' (1975) pp. 1061–1083</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> L. Gross, "Logarithmic Sobolev inequalities and contractivity properties of semigroups" G. Dell'Antonio (ed.) U. Mosco (ed.) , ''Dirichlet Forms'' , ''Lecture Notes in Mathematics'' , '''1563''' , Springer (1993) pp. 54–88</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> E. Nelson, "A quartic interaction in two dimensions" R. Goodman (ed.) I.E. Segal (ed.) , ''Mathematical Theory of Elementary Particles'' , MIT (1966) pp. 69–73</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> D. Stroock, "Logarithmic Sobolev inequalities for Gibbs states" G. Dell'Antonio (ed.) U. Mosco (ed.) , ''Dirichlet Forms'' , ''Lecture Notes in Mathematics'' , '''1563''' , Springer (1993) pp. 194–228</TD></TR></table> | ||
Latest revision as of 22:11, 5 June 2020
A semi-group $ e ^ {- tH } $
of Hermitian operators (cf. also Semi-group of operators) on a Hilbert space $ L _ {2} ( X, \mu ) $
such that:
1) $ \| {e ^ {- tH } f } \| _ {L _ {p} } \leq \| f \| _ {L _ {p} } $ for all $ t > 0 $, $ p \in [ 1, \infty ] $ and $ f \in L _ {2} $;
2) there exist $ T > 0 $ and $ b < \infty $ such that $ \| {e ^ {- TH } f } \| _ {L _ {4} } \leq b \| f \| _ {L _ {2} } $ for all $ f \in L _ {2} $. Semi-groups having properties similar to 1) and 2) were first introduced by E. Nelson [a9] to prove that the Hamiltonian operators arising in some models of quantum field theory are bounded below. In the important case that $ \mu ( X ) < \infty $, condition 2) can be replaced by the following more natural condition, to which 2) is equivalent in the presence of 1):
3) for every $ p,q \in ( 1, \infty ) $ there exists a $ t = t ( p,q ) $, depending on $ p $ and $ q $, such that $ e ^ {- tH } $( restricted or extended to $ L _ {p} $) is a bounded operator from $ L _ {p} ( X, \mu ) $ to $ L _ {q} ( X, \mu ) $. Interpolation theorems are used in the proof. Below, all $ L _ {p} $ spaces are taken to be real for simplicity and it is assumed that $ \mu ( X ) = 1 $, this being the case of principal interest.
The prototypical example of a hypercontractive semi-group is given by choosing $ X = \mathbf R ^ {n} $ and
$$ d \mu ( x ) = ( 2 \pi ) ^ {- n/2 } e ^ {- { {\left | x \right | ^ {2} } / 2 } } dx. $$
Denote by $ ( {\partial / {\partial x _ {j} } } ) ^ {*} $ the adjoint of differentiation computed in $ L _ {2} ( \mathbf R ^ {n} , \mu ) $. Let
$$ H = { \frac{1}{2} } \sum _ {j = 1 } ^ { n } \left ( { \frac \partial {\partial x _ {j} } } \right ) ^ {*} { \frac \partial {\partial x _ {j} } } . $$
(This should be interpreted as a closed version of the Ornstein–Uhlenbeck operator with $ C _ {c} ^ \infty $ as a core.) Then $ e ^ {- tH } $ is a hypercontractive semi-group. In fact, $ b $ can be taken equal to one in condition 2). Furthermore, for this semi-group the smallest time $ t $ for boundedness in condition 3) is known. One has Nelson's family of hypercontractive inequalities: for $ 1 < p \leq q < \infty $,
$$ \tag{a1 } \left \| {e ^ {- tH } } \right \| _ {L _ {p} \rightarrow L _ {q} } \leq 1 \iff e ^ {- 2t } \leq { \frac{( p - 1 ) }{( q - 1 ) } } . $$
Moreover, $ \| {e ^ {- tH } } \| _ {L _ {p} \rightarrow L _ {q} } = \infty $ if $ e ^ {- 2t } > { {( p - 1 ) } / {( q - 1 ) } } $. In (a1) one should regard the operators $ e ^ {- tH } $ as restricted or extended to $ L _ {p} $.
If in (a1) one chooses $ p = 2 $ and $ q = q ( t ) = 1 + e ^ {2t } $, then (a1) yields
$$ \tag{a2 } \left \| {e ^ {- tH } f } \right \| _ {L _ {q ( t ) } } \leq \left \| f \right \| _ {L _ {2} } \textrm{ for } t \geq 0, f \in L _ {2} ( \mathbf R ^ {n} , \mu ) . $$
This inequality becomes an equality for $ t = 0 $. Therefore it can be differentiated at $ t = 0 $ for $ f $ smooth enough. One gets the following logarithmic Sobolev inequality [a7]:
$$ \tag{a3 } \int\limits _ {\mathbf R ^ {n} } {\left | {f ( x ) } \right | ^ {2} { \mathop{\rm ln} } \left | {f ( x ) } \right | } {d \mu ( x ) } \leq $$
$$ \leq \int\limits _ {\mathbf R ^ {n} } {\left | { { \mathop{\rm grad} } f ( x ) } \right | ^ {2} } {d \mu ( x ) } + \left \| f \right \| _ {L _ {2} } ^ {2} { \mathop{\rm ln} } \left \| f \right \| _ {L _ {2} } . $$
Nelson's family of hypercontractive inequalities (a1) can be recovered easily from the single logarithmic Sobolev inequality (a3) [a7]. More generally, L. Gross [a7] established an equivalence between hypercontractivity conditions such as 1) and 2), on the one hand, and, on the other hand, coercivity inequalities for $ H $ of the form
$$ \tag{a4 } \int\limits _ { X } {\left | {f ( x ) } \right | ^ {2} { \mathop{\rm ln} } \left | {f ( x ) } \right | } {d \mu ( x ) } \leq $$
$$ \leq c ( Hf,f ) + m \left \| f \right \| ^ {2} _ {L _ {2} } + \left \| f \right \| ^ {2} _ {L _ {2} } { \mathop{\rm ln} } \left \| f \right \| _ {L _ {2} } $$
(which reduces to (a3) in the previous example if one takes $ c = 1 $ and $ m = 0 $). These coercivity inequalities have come to be known in general as logarithmic Sobolev inequalities. Because of this equivalence the theory of hypercontractive semi-groups has, to a great extent, been developed in conjunction with the theory of logarithmic Sobolev inequalities. The equivalence of (a4) with 1) and 2) is valid only for a class of operators $ H $ which includes the important category of Dirichlet-form operators. See the survey [a8] for further generality and for references to the early history of these two topics.
By way of application, if one can establish inequalities of the form (a4) for an elliptic partial differential operator $ H $ on a Riemannian manifold, then one half of the equivalence theorem shows that the semi-group $ e ^ {- tH } $ has boundedness properties similar to 3), with a specifically given function $ t ( p,q ) $. Since $ e ^ {- tH } $ is an integral operator, with kernel $ K _ {t} ( x,y ) $ say, these norm bounds on $ e ^ {- tH } $ can be converted into direct estimates on the size of the so-called "heat kernel" $ K _ {t} ( x,y ) $. See [a4] for a self-contained exposition of this method of obtaining pointwise heat kernel bounds for elliptic partial differential operators.
There are three basic consequences of the logarithmic Sobolev inequality (a4) which do not require $ H $ to be a Dirichlet-form operator but merely self-adjoint (cf. Self-adjoint operator).
i) The Federbush–Faris semi-boundedness theorem asserts that (a4) is equivalent to the condition that the (generally unbounded) operator $ H + V $ is in fact bounded below for all real-valued measurable functions $ V $ on $ X $ satisfying $ \| {e ^ {- V } } \| _ {L _ {2} ( \mu ) } < \infty $.
ii) The Segal–Faris additivity theorem asserts that if $ H _ {1} $ and $ H _ {2} $ both satisfy (a4), then so does the independent sum $ H _ {1} \otimes I + I \otimes H _ {2} $.
iii) The Rothaus–Simon spectral gap theorem asserts that if (a4) holds with $ m = 0 $ and if $ H1 = 0 $, then $ H $ has no spectrum (cf. Spectrum of an operator) in the interval $ ( 0,c ^ {- 1 } ) $. For precise statements of these theorems and proofs see the survey [a8].
A very simple example of another semi-group satisfying Nelson's hypercontractivity inequalities (a1) is as follows. Denote by $ X $ the two-point set $ \{ - 1,1 \} $. Define $ \mu ( \{ - 1 \} ) = \mu ( \{ 1 \} ) = {1 / 2 } $. Let $ H $ be the projection onto the orthogonal complement of the constant functions in $ L _ {2} ( X, \mu ) $. Then (a1) holds. Moreover, (a4) holds with $ c = 1 $ and $ m = 0 $. Since $ L _ {2} ( X, \mu ) $ is two-dimensional, the proof of (a4) reduces in this example to a few lines of elementary calculus (see, e.g., [a8], Example 2.6). The resulting inequality is known as the two-point logarithmic Sobolev inequality. Now, by the Segal–Faris additivity theorem there follows by induction a logarithmic Sobolev inequality on the product space $ \{ - 1,1 \} ^ {k} $ for the product measure. An application of the central limit theorem then allows one to take the limit as $ k \rightarrow \infty $ and arrive at the inequality (a3) (first for $ n = 1 $, then, by additivity, for general $ n $). This method of deriving the differential inequalities (a1) from discrete inequalities via the central limit theorem [a3], [a7] has also been used [a2] to derive the sharp Hausdorff–Young inequality (cf. Hausdorff–Young inequalities) for the Fourier transform on $ \mathbf R ^ {n} $.
The notions of hypercontractivity and logarithmic Sobolev inequalities can also be formulated in the context of non-commutative integration theory, specifically over Clifford algebras (cf. Clifford algebra). See [a8], Sect. 6(v), for a survey.
Applications of both concepts to statistical mechanics are rapidly increasing at the present time (1996). For a survey of work through 1992, see [a10]. For applications to the theory of large deviations, see [a5]. For recent applications to statistics, see the survey [a6].
Unlike the classical Sobolev inequalities, logarithmic Sobolev inequalities tend to be dimension independent and valid in many infinite-dimensional settings. For example, the inequality (a3) is meaningful and correct when $ n = \infty $. One need only interpret the first integrand on the right as
$$ \sum _ {k = 1 } ^ \infty \left | { { \frac{\partial f }{\partial x _ {k} } } } \right | ^ {2} . $$
The dimension independence accounts, in part, for their usefulness in statistical mechanics (cf. also Statistical mechanics, mathematical problems in), statistics, and large deviations, and for their origin in constructive quantum field theory.
The survey [a8] discusses the topics up through 1992. [a1] also surveys related topics and describes various methods for proving logarithmic Sobolev inequalities for specific operators $ H $.
References
| [a1] | D. Bakry, "L'hypercontractivité et son utilisation en théorie des semi-groups" P. Bernard (ed.) , Lectures on Probability Theory , Lecture Notes in Mathematics , 1581 , Springer (1994) pp. 1–114 |
| [a2] | W. Beckner, "Inequalities in Fourier analysis" Ann. of Math. , 102 (1975) pp. 159–182 |
| [a3] | A. Bonami, "Études des coefficients de Fourier des fonctions de 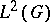 " Ann. Inst. Fourier , 20 : 2 (1970) pp. 335–402 " Ann. Inst. Fourier , 20 : 2 (1970) pp. 335–402 |
| [a4] | E.B. Davies, "Heat kernels and spectral theory" , Cambridge Univ. Press (1989) |
| [a5] | J. D. Deuschel, D. W. Stroock, "Large deviations" , Pure Appl. Math. , 137 , Acad. Press (1989) |
| [a6] | P. Diaconis, L. Saloff-Coste, "Logarithmic Sobolev inequalities for finite Markov chains" Ann. Appl. Probab. (1996) |
| [a7] | L. Gross, "Logarithmic Sobolev inequalities" Amer. J. of Math. , 97 (1975) pp. 1061–1083 |
| [a8] | L. Gross, "Logarithmic Sobolev inequalities and contractivity properties of semigroups" G. Dell'Antonio (ed.) U. Mosco (ed.) , Dirichlet Forms , Lecture Notes in Mathematics , 1563 , Springer (1993) pp. 54–88 |
| [a9] | E. Nelson, "A quartic interaction in two dimensions" R. Goodman (ed.) I.E. Segal (ed.) , Mathematical Theory of Elementary Particles , MIT (1966) pp. 69–73 |
| [a10] | D. Stroock, "Logarithmic Sobolev inequalities for Gibbs states" G. Dell'Antonio (ed.) U. Mosco (ed.) , Dirichlet Forms , Lecture Notes in Mathematics , 1563 , Springer (1993) pp. 194–228 |
Hypercontractive semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hypercontractive_semi-group&oldid=15980