Difference between revisions of "Fock space"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | f0406901.png | ||
| + | $#A+1 = 103 n = 1 | ||
| + | $#C+1 = 103 : ~/encyclopedia/old_files/data/F040/F.0400690 Fock space, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''Fok space'' | ''Fok space'' | ||
In the simplest and most often used case, a [[Hilbert space|Hilbert space]] consisting of infinite sequences of the form | In the simplest and most often used case, a [[Hilbert space|Hilbert space]] consisting of infinite sequences of the form | ||
| − | + | $$ \tag{1 } | |
| + | F = \{ f _ {0} , f _ {1} \dots f _ {n} ,\dots \} , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | f _ {0} \in \mathbf C ,\ \ | ||
| + | f _ {1} \in L _ {2} ( \mathbf R ^ \nu , d ^ \nu x),\ \ | ||
| + | f _ {n} \in L _ {2} ^ {s} (( \mathbf R ^ \nu ) ^ {n} ,\ | ||
| + | ( d ^ \nu x) ^ {n} ), | ||
| + | $$ | ||
or | or | ||
| − | + | $$ | |
| + | f _ {n} \in L _ {2} ^ {a} (( \mathbf R ^ \nu ) ^ {n} ,\ | ||
| + | ( d ^ \nu x) ^ {n} ),\ \ | ||
| + | n = 2, 3 \dots \ \ | ||
| + | \nu = 1, 2 \dots | ||
| + | $$ | ||
in which | in which | ||
| − | + | $$ | |
| + | L _ {2} ^ {s} (( \mathbf R ^ \nu ) ^ {n} , ( d ^ \nu x) ^ {n} ) \ \ | ||
| + | ( \textrm{ or } \ \ | ||
| + | L _ {2} ^ {a} (( \mathbf R ^ \nu ) ^ {n} , ( d ^ \nu x) ^ {n} )) | ||
| + | $$ | ||
| − | denotes the Hilbert space of symmetric (respectively, anti-symmetric) functions in | + | denotes the Hilbert space of symmetric (respectively, anti-symmetric) functions in $ n $ |
| + | variables $ x _ {1} \dots x _ {n} \in \mathbf R ^ \nu $, | ||
| + | $ n = 2, 3 ,\dots $. | ||
| + | The scalar product of two sequences $ F $ | ||
| + | and $ G $ | ||
| + | of the form (1) is equal to | ||
| − | + | $$ | |
| + | ( F, G) = \ | ||
| + | f _ {0} \overline{g}\; _ {0} + | ||
| + | \sum _ {n = 1 } ^ \infty | ||
| + | ( f _ {n} , g _ {n} ) _ {L _ {2} (( \mathbf R ^ \nu ) ^ {n} , ( d ^ \nu x) ^ {n} ) } . | ||
| + | $$ | ||
| − | In the case when the sequences | + | In the case when the sequences $ F $ |
| + | consist of symmetric functions, one speaks of a symmetric (or boson) Fock space, and in the case of sequences of anti-symmetric functions the Fock space is called anti-symmetric (or fermion). Fock spaces were first introduced by V.A. Fock [V.A. Fok] [[#References|[1]]] in this simplest case. | ||
| − | In the general case of an arbitrary Hilbert space | + | In the general case of an arbitrary Hilbert space $ H $, |
| + | the Fock space $ \Gamma ^ {s} ( H) $( | ||
| + | or $ \Gamma ^ {a} ( H) $) | ||
| + | constructed over $ H $ | ||
| + | is the symmetrized (or anti-symmetrized) tensor exponential of $ H $, | ||
| + | that is, the space | ||
| − | + | $$ \tag{2 } | |
| + | \Gamma ^ \alpha ( H) \equiv \ | ||
| + | \mathop{\rm Exp} _ \alpha H = \oplus | ||
| + | \sum _ {n = 0 } ^ \infty | ||
| + | ( H ^ {\otimes n } ) _ \alpha ,\ \ | ||
| + | \alpha = s, a, | ||
| + | $$ | ||
| − | where the symbol | + | where the symbol $ \oplus $ |
| + | denotes the direct orthogonal sum of Hilbert spaces, $ ( H ^ {\otimes 0 } ) _ \alpha = \mathbf C ^ {1} $, | ||
| + | $ ( H ^ {\otimes 1 } ) _ \alpha = H $, | ||
| + | and $ ( H ^ {\otimes n } ) _ \alpha $, | ||
| + | $ n > 1 $, | ||
| + | is for $ \alpha = s $ | ||
| + | the symmetrized or for $ \alpha = a $ | ||
| + | the anti-symmetrized $ n $- | ||
| + | th tensor power of $ H $. | ||
| + | In the case $ H = L _ {2} ( \mathbf R ^ \nu , d ^ \nu x) $ | ||
| + | definition (2) is equivalent to the definition of a Fock space given at the beginning of the article, if one identifies the spaces $ L _ {2} ^ \alpha (( \mathbf R ^ \nu ) ^ {n} , ( d ^ \nu x) ^ {n} ) $ | ||
| + | and $ ( L _ {2} ( \mathbf R ^ \nu , d ^ \nu x)) _ \alpha ^ {\otimes n } $ | ||
| + | so that the tensor product | ||
| − | + | $$ | |
| + | ( f _ {1} \otimes \dots \otimes f _ {n} ) _ \alpha \ | ||
| + | \in ( L _ {2} ( \mathbf R ^ \nu , d ^ \nu x)) _ \alpha ^ {\otimes n } | ||
| + | $$ | ||
of the sequence of functions | of the sequence of functions | ||
| − | + | $$ | |
| + | f _ {1} \dots f _ {n} \in \ | ||
| + | L _ {2} ( \mathbf R ^ \nu , d ^ \nu x) | ||
| + | $$ | ||
corresponds to the function | corresponds to the function | ||
| − | + | $$ \tag{3 } | |
| + | { | ||
| + | \frac{1}{\sqrt n! } | ||
| + | } | ||
| + | \sum _ \sigma | ||
| + | ( \pm 1) ^ { \mathop{\rm sign} \sigma } | ||
| + | \prod _ {i = 1 } ^ { n } | ||
| + | f ( x _ {\sigma ( i) } ) \in \ | ||
| + | L _ {2} ^ \alpha (( \mathbf R ^ \nu ) ^ \nu , ( d ^ \nu x) ^ {n} ), | ||
| + | $$ | ||
| − | where the summation is taken over all permutations | + | where the summation is taken over all permutations $ \sigma $ |
| + | of the indices $ 1 \dots n $; | ||
| + | $ \mathop{\rm sign} \sigma $ | ||
| + | is the sign of $ \sigma $, | ||
| + | and the sign $ + 1 $ | ||
| + | or $ - 1 $ | ||
| + | in (3) corresponds to the symmetric or anti-symmetric case. | ||
| − | In quantum mechanics, the Fock spaces | + | In quantum mechanics, the Fock spaces $ \Gamma ^ {s} ( H) $ |
| + | or $ \Gamma ^ {a} ( H) $ | ||
| + | serve as the state spaces of quantum-mechanical systems consisting of an arbitrary (but finite) number of identical particles such that the state space of each separate particle is $ H $. | ||
| + | Here, depending on which of the Fock spaces — the symmetric $ \Gamma ^ {s} ( H) $ | ||
| + | or the anti-symmetric $ \Gamma ^ {a} ( H) $— | ||
| + | describes this system, the particles themselves are called bosons or fermions, respectively. For every $ n = 1, 2 \dots $ | ||
| + | the subspace $ \Gamma _ {n} ^ \alpha ( H) \equiv ( H ^ {\otimes n } ) _ \alpha \subset \Gamma ^ \alpha ( H) $, | ||
| + | $ \alpha = s, a $, | ||
| + | is called the $ n $- | ||
| + | particle subspace: The vectors in it describe those states in which there are exactly $ n $ | ||
| + | particles; the unit vector $ \Omega \in ( H ^ {\otimes 0 } ) _ \alpha \subset \Gamma ^ \alpha ( H) $, | ||
| + | $ \alpha = s, a $( | ||
| + | in the notation of (1): $ \Omega = \{ 1, 0 \dots 0 ,\dots \} $), | ||
| + | called the vacuum vector, describes the state of the system in which there are no particles. | ||
| − | In studying linear operators acting on the Fock spaces | + | In studying linear operators acting on the Fock spaces $ \Gamma ^ {s} ( H) $ |
| + | and $ \Gamma ^ {a} ( H) $, | ||
| + | one often applies a special formalism called the method of second quantization. It is based on introducing two families of linear operators on each of the spaces $ \Gamma ^ \alpha ( H) $: | ||
| + | the so-called [[Annihilation operators|annihilation operators]] $ \{ {a _ \alpha ( f ) } : {f \in H } \} $, | ||
| + | $ \alpha = s, a $, | ||
| + | and the family of operators adjoint to them $ \{ {a _ \alpha ^ {*} ( f ) } : {f \in H } \} $, | ||
| + | called [[Creation operators|creation operators]]. The annihilation operators are given as the closures of the operators acting on the vectors | ||
| − | + | $$ \tag{4 } | |
| + | ( f _ {1} \otimes \dots \otimes f _ {n} ) _ \alpha \ | ||
| + | \in \Gamma ^ \alpha ( H),\ \ | ||
| + | \alpha = s, a, | ||
| + | $$ | ||
| − | where | + | where $ ( f _ {1} \otimes \dots \otimes f _ {n} ) _ \alpha $ |
| + | are the symmetrized (for $ \alpha = s $) | ||
| + | or anti-symmetrized $ ( \alpha = a) $ | ||
| + | tensor products of the sequences of vectors $ f _ {1} \dots f _ {n} \in H $, | ||
| + | $ n = 1, 2 \dots $ | ||
| + | according to the formulas | ||
| − | + | $$ | |
| + | a _ \alpha ( f ) | ||
| + | ( f _ {1} \otimes \dots \otimes f _ {n} ) _ \alpha = \ | ||
| + | \sum _ {i = 1 } ^ { n } | ||
| + | (- 1) ^ {g _ \alpha ( i) } | ||
| + | ( f _ {i} , f ) \times | ||
| + | $$ | ||
| − | + | $$ | |
| + | \times | ||
| + | ( f _ {1} \otimes \dots \otimes f _ {i - 1 } \otimes f _ {i + 1 } \otimes \dots \otimes f _ {n} ) _ \alpha , | ||
| + | $$ | ||
| − | + | $$ | |
| + | \alpha = s , a,\ a _ \alpha ( f ) \Omega = 0, | ||
| + | $$ | ||
| − | where | + | where $ g _ {s} ( i) = 0 $ |
| + | and $ g _ {a} ( i) = i - 1 $. | ||
| + | The creation operators $ a _ \alpha ^ {*} ( f ) $ | ||
| + | act on the vectors (3) according to the formulas | ||
| − | + | $$ | |
| + | a _ \alpha ^ {*} ( f ) | ||
| + | ( f _ {1} \otimes \dots \otimes f _ {n} ) _ \alpha = \ | ||
| + | ( f \otimes f _ {1} \otimes \dots \otimes f _ {n} ) _ \alpha , | ||
| + | $$ | ||
| − | + | $$ | |
| + | a _ \alpha ^ {*} ( f ) \Omega = f. | ||
| + | $$ | ||
| − | Here for every | + | Here for every $ f \in H $, |
| + | $ a _ \alpha ( f ) $: | ||
| + | $ \Gamma _ {n} ^ \alpha ( H) \rightarrow \Gamma _ {n - 1 } ^ \alpha ( H) $, | ||
| + | $ n = 1, 2 \dots $ | ||
| + | and $ a _ \alpha ^ {*} ( f ): \Gamma _ {n} ^ \alpha ( H) \rightarrow \Gamma _ {n + 1 } ^ {a} ( H) $, | ||
| + | $ n = 0, 1 \dots $ | ||
| + | that is, states of the physical system with $ n $ | ||
| + | particles are mapped by the annihilation operators $ a _ \alpha ( f ) $ | ||
| + | to states with $ ( n - 1) $ | ||
| + | particles, and by the creation operators $ a _ \alpha ^ {*} ( f ) $ | ||
| + | to states with $ ( n + 1) $ | ||
| + | particles. Creation and annihilation operators occur in many cases of a similar system as "generators" in the collection of all operators (bounded and unbounded) acting on Fock spaces. The representation of such operators in the form of a sum (finite or infinite) of operators of the form | ||
| − | + | $$ | |
| + | a _ \alpha ^ {*} ( f _ {1} ) \dots | ||
| + | a _ \alpha ^ {*} ( f _ {n} ) | ||
| + | a _ \alpha ( g _ {1} ) \dots | ||
| + | a _ \alpha ( g _ {m} ) | ||
| + | $$ | ||
| − | + | $$ | |
| + | ( f _ {1} \dots f _ {n} , g _ {1} \dots g _ {m} \in H,\ n, m = 0, 1 ,\dots) | ||
| + | $$ | ||
— the so-called normal form of an operator — and methods of dealing with operators based on such a representation (computing functions of them, reducing operators to the "simplest" form, various examples of approximation, etc.) also constitute the content of the formalism of second quantization mentioned above (see [[#References|[2]]]). | — the so-called normal form of an operator — and methods of dealing with operators based on such a representation (computing functions of them, reducing operators to the "simplest" form, various examples of approximation, etc.) also constitute the content of the formalism of second quantization mentioned above (see [[#References|[2]]]). | ||
| − | In the case of a symmetric Fock space over a real space | + | In the case of a symmetric Fock space over a real space $ H $ |
| + | there is a canonical isomorphism between that space and the Hilbert space of square-integrable functionals in a Gaussian linear random process $ \{ {\xi _ {f} } : {f \in H } \} $ | ||
| + | defined on $ H $ | ||
| + | such that | ||
| − | + | $$ | |
| + | M _ {\xi _ {f} } = 0,\ \ | ||
| + | M ( \xi _ {f _ {1} } \xi _ {f _ {2} } ) = \ | ||
| + | ( f _ {1} , f _ {2} ) _ {H} ,\ \ | ||
| + | f, f _ {1} , f _ {2} \in H. | ||
| + | $$ | ||
| − | This isomorphism, called the Itô–Segal–Wick mapping, is uniquely determined by the condition that for any orthonormal system of elements | + | This isomorphism, called the Itô–Segal–Wick mapping, is uniquely determined by the condition that for any orthonormal system of elements $ f _ {1} \dots f _ {k} \in H $ |
| + | and any collection of non-negative integers $ n _ {1} \dots n _ {k} $ | ||
| + | the vector | ||
| − | + | $$ | |
| + | f _ {1} \otimes \dots \otimes | ||
| + | f _ {1} \otimes \dots \otimes | ||
| + | f _ {k} \otimes \dots \otimes | ||
| + | f _ {k} \in \ | ||
| + | \Gamma ^ {s} ( H) | ||
| + | $$ | ||
| − | ( | + | ( $ n _ {1} $ |
| + | times $ f _ {1} \dots n _ {k} $ | ||
| + | times $ f _ {k} $) | ||
| + | is mapped to the functional | ||
| − | + | $$ | |
| + | \prod _ {i = 1 } ^ { k } | ||
| + | H _ {n _ {i} } | ||
| + | ( \xi _ {f _ {i} } ), | ||
| + | $$ | ||
| − | where the | + | where the $ H _ {n} ( \cdot ) $, |
| + | $ n = 0, 1 \dots $ | ||
| + | are the Hermite polynomials with leading coefficient one (see [[#References|[3]]], [[#References|[4]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> V. Fock, ''Z. Phys.'' , '''75''' (1932) pp. 622–647</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> F.A. Berezin, "The method of second quantization" , Acad. Press (1966) (Translated from Russian) (Revised (augmented) second edition: Kluwer, 1989)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R.L. Dobrushin, R.A. Minlos, "Polynomials in linear random functions" ''Russian Math. Surveys'' , '''32''' : 2 (1971) pp. 71–127 ''Uspekhi Mat. Nauk'' , '''32''' : 2 (1977) pp. 67–122</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B. Simon, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040690/f04069099.png" /> Euclidean (quantum) field theory" , Princeton Univ. Press (1974)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> V. Fock, ''Z. Phys.'' , '''75''' (1932) pp. 622–647</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> F.A. Berezin, "The method of second quantization" , Acad. Press (1966) (Translated from Russian) (Revised (augmented) second edition: Kluwer, 1989)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R.L. Dobrushin, R.A. Minlos, "Polynomials in linear random functions" ''Russian Math. Surveys'' , '''32''' : 2 (1971) pp. 71–127 ''Uspekhi Mat. Nauk'' , '''32''' : 2 (1977) pp. 67–122</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B. Simon, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040690/f04069099.png" /> Euclidean (quantum) field theory" , Princeton Univ. Press (1974)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | The number operator | + | The number operator $ \sum _ {f} a _ \alpha ^ {*} ( f ) a _ \alpha ( f ) $, |
| + | $ \alpha = a , s $, | ||
| + | where $ f $ | ||
| + | runs through an orthonormal basis of $ H $, | ||
| + | has as eigen spaces with eigen value $ n $ | ||
| + | the spaces $ \Gamma _ {n} ^ \alpha ( H) $. | ||
| + | It is interpreted as giving the number of particles. | ||
Fock spaces also play an important role in stochastic integration (including fermionic integration), cf. [[Stochastic integral|Stochastic integral]], and in [[White noise|white noise]] analysis. | Fock spaces also play an important role in stochastic integration (including fermionic integration), cf. [[Stochastic integral|Stochastic integral]], and in [[White noise|white noise]] analysis. | ||
Latest revision as of 19:39, 5 June 2020
Fok space
In the simplest and most often used case, a Hilbert space consisting of infinite sequences of the form
$$ \tag{1 } F = \{ f _ {0} , f _ {1} \dots f _ {n} ,\dots \} , $$
where
$$ f _ {0} \in \mathbf C ,\ \ f _ {1} \in L _ {2} ( \mathbf R ^ \nu , d ^ \nu x),\ \ f _ {n} \in L _ {2} ^ {s} (( \mathbf R ^ \nu ) ^ {n} ,\ ( d ^ \nu x) ^ {n} ), $$
or
$$ f _ {n} \in L _ {2} ^ {a} (( \mathbf R ^ \nu ) ^ {n} ,\ ( d ^ \nu x) ^ {n} ),\ \ n = 2, 3 \dots \ \ \nu = 1, 2 \dots $$
in which
$$ L _ {2} ^ {s} (( \mathbf R ^ \nu ) ^ {n} , ( d ^ \nu x) ^ {n} ) \ \ ( \textrm{ or } \ \ L _ {2} ^ {a} (( \mathbf R ^ \nu ) ^ {n} , ( d ^ \nu x) ^ {n} )) $$
denotes the Hilbert space of symmetric (respectively, anti-symmetric) functions in $ n $ variables $ x _ {1} \dots x _ {n} \in \mathbf R ^ \nu $, $ n = 2, 3 ,\dots $. The scalar product of two sequences $ F $ and $ G $ of the form (1) is equal to
$$ ( F, G) = \ f _ {0} \overline{g}\; _ {0} + \sum _ {n = 1 } ^ \infty ( f _ {n} , g _ {n} ) _ {L _ {2} (( \mathbf R ^ \nu ) ^ {n} , ( d ^ \nu x) ^ {n} ) } . $$
In the case when the sequences $ F $ consist of symmetric functions, one speaks of a symmetric (or boson) Fock space, and in the case of sequences of anti-symmetric functions the Fock space is called anti-symmetric (or fermion). Fock spaces were first introduced by V.A. Fock [V.A. Fok] [1] in this simplest case.
In the general case of an arbitrary Hilbert space $ H $, the Fock space $ \Gamma ^ {s} ( H) $( or $ \Gamma ^ {a} ( H) $) constructed over $ H $ is the symmetrized (or anti-symmetrized) tensor exponential of $ H $, that is, the space
$$ \tag{2 } \Gamma ^ \alpha ( H) \equiv \ \mathop{\rm Exp} _ \alpha H = \oplus \sum _ {n = 0 } ^ \infty ( H ^ {\otimes n } ) _ \alpha ,\ \ \alpha = s, a, $$
where the symbol $ \oplus $ denotes the direct orthogonal sum of Hilbert spaces, $ ( H ^ {\otimes 0 } ) _ \alpha = \mathbf C ^ {1} $, $ ( H ^ {\otimes 1 } ) _ \alpha = H $, and $ ( H ^ {\otimes n } ) _ \alpha $, $ n > 1 $, is for $ \alpha = s $ the symmetrized or for $ \alpha = a $ the anti-symmetrized $ n $- th tensor power of $ H $. In the case $ H = L _ {2} ( \mathbf R ^ \nu , d ^ \nu x) $ definition (2) is equivalent to the definition of a Fock space given at the beginning of the article, if one identifies the spaces $ L _ {2} ^ \alpha (( \mathbf R ^ \nu ) ^ {n} , ( d ^ \nu x) ^ {n} ) $ and $ ( L _ {2} ( \mathbf R ^ \nu , d ^ \nu x)) _ \alpha ^ {\otimes n } $ so that the tensor product
$$ ( f _ {1} \otimes \dots \otimes f _ {n} ) _ \alpha \ \in ( L _ {2} ( \mathbf R ^ \nu , d ^ \nu x)) _ \alpha ^ {\otimes n } $$
of the sequence of functions
$$ f _ {1} \dots f _ {n} \in \ L _ {2} ( \mathbf R ^ \nu , d ^ \nu x) $$
corresponds to the function
$$ \tag{3 } { \frac{1}{\sqrt n! } } \sum _ \sigma ( \pm 1) ^ { \mathop{\rm sign} \sigma } \prod _ {i = 1 } ^ { n } f ( x _ {\sigma ( i) } ) \in \ L _ {2} ^ \alpha (( \mathbf R ^ \nu ) ^ \nu , ( d ^ \nu x) ^ {n} ), $$
where the summation is taken over all permutations $ \sigma $ of the indices $ 1 \dots n $; $ \mathop{\rm sign} \sigma $ is the sign of $ \sigma $, and the sign $ + 1 $ or $ - 1 $ in (3) corresponds to the symmetric or anti-symmetric case.
In quantum mechanics, the Fock spaces $ \Gamma ^ {s} ( H) $ or $ \Gamma ^ {a} ( H) $ serve as the state spaces of quantum-mechanical systems consisting of an arbitrary (but finite) number of identical particles such that the state space of each separate particle is $ H $. Here, depending on which of the Fock spaces — the symmetric $ \Gamma ^ {s} ( H) $ or the anti-symmetric $ \Gamma ^ {a} ( H) $— describes this system, the particles themselves are called bosons or fermions, respectively. For every $ n = 1, 2 \dots $ the subspace $ \Gamma _ {n} ^ \alpha ( H) \equiv ( H ^ {\otimes n } ) _ \alpha \subset \Gamma ^ \alpha ( H) $, $ \alpha = s, a $, is called the $ n $- particle subspace: The vectors in it describe those states in which there are exactly $ n $ particles; the unit vector $ \Omega \in ( H ^ {\otimes 0 } ) _ \alpha \subset \Gamma ^ \alpha ( H) $, $ \alpha = s, a $( in the notation of (1): $ \Omega = \{ 1, 0 \dots 0 ,\dots \} $), called the vacuum vector, describes the state of the system in which there are no particles.
In studying linear operators acting on the Fock spaces $ \Gamma ^ {s} ( H) $ and $ \Gamma ^ {a} ( H) $, one often applies a special formalism called the method of second quantization. It is based on introducing two families of linear operators on each of the spaces $ \Gamma ^ \alpha ( H) $: the so-called annihilation operators $ \{ {a _ \alpha ( f ) } : {f \in H } \} $, $ \alpha = s, a $, and the family of operators adjoint to them $ \{ {a _ \alpha ^ {*} ( f ) } : {f \in H } \} $, called creation operators. The annihilation operators are given as the closures of the operators acting on the vectors
$$ \tag{4 } ( f _ {1} \otimes \dots \otimes f _ {n} ) _ \alpha \ \in \Gamma ^ \alpha ( H),\ \ \alpha = s, a, $$
where $ ( f _ {1} \otimes \dots \otimes f _ {n} ) _ \alpha $ are the symmetrized (for $ \alpha = s $) or anti-symmetrized $ ( \alpha = a) $ tensor products of the sequences of vectors $ f _ {1} \dots f _ {n} \in H $, $ n = 1, 2 \dots $ according to the formulas
$$ a _ \alpha ( f ) ( f _ {1} \otimes \dots \otimes f _ {n} ) _ \alpha = \ \sum _ {i = 1 } ^ { n } (- 1) ^ {g _ \alpha ( i) } ( f _ {i} , f ) \times $$
$$ \times ( f _ {1} \otimes \dots \otimes f _ {i - 1 } \otimes f _ {i + 1 } \otimes \dots \otimes f _ {n} ) _ \alpha , $$
$$ \alpha = s , a,\ a _ \alpha ( f ) \Omega = 0, $$
where $ g _ {s} ( i) = 0 $ and $ g _ {a} ( i) = i - 1 $. The creation operators $ a _ \alpha ^ {*} ( f ) $ act on the vectors (3) according to the formulas
$$ a _ \alpha ^ {*} ( f ) ( f _ {1} \otimes \dots \otimes f _ {n} ) _ \alpha = \ ( f \otimes f _ {1} \otimes \dots \otimes f _ {n} ) _ \alpha , $$
$$ a _ \alpha ^ {*} ( f ) \Omega = f. $$
Here for every $ f \in H $, $ a _ \alpha ( f ) $: $ \Gamma _ {n} ^ \alpha ( H) \rightarrow \Gamma _ {n - 1 } ^ \alpha ( H) $, $ n = 1, 2 \dots $ and $ a _ \alpha ^ {*} ( f ): \Gamma _ {n} ^ \alpha ( H) \rightarrow \Gamma _ {n + 1 } ^ {a} ( H) $, $ n = 0, 1 \dots $ that is, states of the physical system with $ n $ particles are mapped by the annihilation operators $ a _ \alpha ( f ) $ to states with $ ( n - 1) $ particles, and by the creation operators $ a _ \alpha ^ {*} ( f ) $ to states with $ ( n + 1) $ particles. Creation and annihilation operators occur in many cases of a similar system as "generators" in the collection of all operators (bounded and unbounded) acting on Fock spaces. The representation of such operators in the form of a sum (finite or infinite) of operators of the form
$$ a _ \alpha ^ {*} ( f _ {1} ) \dots a _ \alpha ^ {*} ( f _ {n} ) a _ \alpha ( g _ {1} ) \dots a _ \alpha ( g _ {m} ) $$
$$ ( f _ {1} \dots f _ {n} , g _ {1} \dots g _ {m} \in H,\ n, m = 0, 1 ,\dots) $$
— the so-called normal form of an operator — and methods of dealing with operators based on such a representation (computing functions of them, reducing operators to the "simplest" form, various examples of approximation, etc.) also constitute the content of the formalism of second quantization mentioned above (see [2]).
In the case of a symmetric Fock space over a real space $ H $ there is a canonical isomorphism between that space and the Hilbert space of square-integrable functionals in a Gaussian linear random process $ \{ {\xi _ {f} } : {f \in H } \} $ defined on $ H $ such that
$$ M _ {\xi _ {f} } = 0,\ \ M ( \xi _ {f _ {1} } \xi _ {f _ {2} } ) = \ ( f _ {1} , f _ {2} ) _ {H} ,\ \ f, f _ {1} , f _ {2} \in H. $$
This isomorphism, called the Itô–Segal–Wick mapping, is uniquely determined by the condition that for any orthonormal system of elements $ f _ {1} \dots f _ {k} \in H $ and any collection of non-negative integers $ n _ {1} \dots n _ {k} $ the vector
$$ f _ {1} \otimes \dots \otimes f _ {1} \otimes \dots \otimes f _ {k} \otimes \dots \otimes f _ {k} \in \ \Gamma ^ {s} ( H) $$
( $ n _ {1} $ times $ f _ {1} \dots n _ {k} $ times $ f _ {k} $) is mapped to the functional
$$ \prod _ {i = 1 } ^ { k } H _ {n _ {i} } ( \xi _ {f _ {i} } ), $$
where the $ H _ {n} ( \cdot ) $, $ n = 0, 1 \dots $ are the Hermite polynomials with leading coefficient one (see [3], [4]).
References
| [1] | V. Fock, Z. Phys. , 75 (1932) pp. 622–647 |
| [2] | F.A. Berezin, "The method of second quantization" , Acad. Press (1966) (Translated from Russian) (Revised (augmented) second edition: Kluwer, 1989) |
| [3] | R.L. Dobrushin, R.A. Minlos, "Polynomials in linear random functions" Russian Math. Surveys , 32 : 2 (1971) pp. 71–127 Uspekhi Mat. Nauk , 32 : 2 (1977) pp. 67–122 |
| [4] | B. Simon, "The 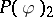 Euclidean (quantum) field theory" , Princeton Univ. Press (1974) Euclidean (quantum) field theory" , Princeton Univ. Press (1974) |
Comments
The number operator $ \sum _ {f} a _ \alpha ^ {*} ( f ) a _ \alpha ( f ) $, $ \alpha = a , s $, where $ f $ runs through an orthonormal basis of $ H $, has as eigen spaces with eigen value $ n $ the spaces $ \Gamma _ {n} ^ \alpha ( H) $. It is interpreted as giving the number of particles.
Fock spaces also play an important role in stochastic integration (including fermionic integration), cf. Stochastic integral, and in white noise analysis.
References
| [a1] | N.N. [N.N. Bogolyubov] Bogolubov, A.A. Logunov, I.T. Todorov, "Introduction to axiomatic quantum field theory" , Benjamin (1975) (Translated from Russian) |
| [a2] | P.J.M. Bongaarts, "The mathematical structure of free quantum fields. Gaussian systems" E.A. de Kerf (ed.) H.G.J. Pijls (ed.) , Proc. Seminar. Mathematical structures in field theory , CWI, Amsterdam (1984–1986) pp. 1–50 |
Fock space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fock_space&oldid=13259