Difference between revisions of "Erdös-Heilbronn problem"
Ulf Rehmann (talk | contribs) m (moved Erdos-Heilbronn problem to Erdös-Heilbronn problem: accented title) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | e1101101.png | ||
| + | $#A+1 = 26 n = 1 | ||
| + | $#C+1 = 26 : ~/encyclopedia/old_files/data/E110/E.1100110 Erd\AGos\ANDHeilbronn problem | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Let $ G $ | |
| + | be an [[Abelian group|Abelian group]] and let $ A \subset G $. | ||
| + | For $ k \in \mathbf N $, | ||
| + | let | ||
| − | + | $$ | |
| + | k \wedge A = \left \{ {\sum _ {x \in X } x } : {X \subset A \textrm{ and } \left | X \right | = k } \right \} . | ||
| + | $$ | ||
| − | + | (Here, $ | A | $ | |
| + | denotes the cardinality of a set $ A $.) | ||
| + | Let $ p $ | ||
| + | be a [[Prime number|prime number]] and let $ A \subset \mathbf Z/p \mathbf Z $. | ||
| + | It was conjectured by P. Erdös and H. Heilbronn that $ | {2 \wedge A } | \geq \min ( p,2 | A | - 3 ) $. | ||
| − | + | This conjecture, mentioned in [[#References|[a5]]], was first proved in [[#References|[a3]]], using [[Linear-algebra(2)|linear algebra]]. As a consequence of the lower bound on the degree of the minimal polynomial of the Grasmann derivative, the following theorem is true [[#References|[a3]]]: Let $ p $ | |
| + | be a prime number and let $ A \subset \mathbf Z/ {p \mathbf Z } $. | ||
| + | Then | ||
| − | + | $$ | |
| + | \left | {k \wedge A } \right | \geq \min ( p,k ( \left | A \right | - k ) + 1 ) . | ||
| + | $$ | ||
| − | This was conjectured partially by Erdös and R. Graham [[#References|[a5]]] and follows easily by applying the conjecture twice, after adding | + | Applying this theorem with $ k = 2 $, |
| + | one obtains the Erdös–Heilbronn conjecture mentioned above. A generalization of the theorem has been obtained in [[#References|[a2]]]. Presently (1996), almost nothing is known for composite numbers. The following conjecture is proposed here: Let $ n $ | ||
| + | be a composite number (cf. also [[Prime number|Prime number]]) and let $ A \subset \mathbf Z/ {n \mathbf Z } $ | ||
| + | be such that $ | A | \geq k - 1 + { {( n - 1 ) } / k } $. | ||
| + | Then $ 0 \in j \wedge A $ | ||
| + | for some $ 1 \leq j \leq k $. | ||
| + | |||
| + | For a prime number $ n $, | ||
| + | the above conjecture is an easy consequence of the theorem above. Some applications to integer subset sums are contained in [[#References|[a6]]]. Along the same lines, the conjecture has several implications. In particular, for $ k = 3 $ | ||
| + | one finds: Let $ A \subset \{ 1 \dots n \} $ | ||
| + | be such that $ | A | \geq 5 + { {( n - 1 ) } / 3 } $. | ||
| + | Then there is a $ B \subset A $ | ||
| + | such that $ 3 \leq | B | \leq 6 $ | ||
| + | and $ \sum _ {x \in B } x = 2n $. | ||
| + | |||
| + | This was conjectured partially by Erdös and R. Graham [[#References|[a5]]] and follows easily by applying the conjecture twice, after adding $ 0 $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N. Alon, "Subset sums" ''J. Number Th.'' , '''27''' (1987) pp. 196–205</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N. Alon, M.B. Nathanson, I. Z. Rusza, "The polynomial method and restricted sums of congruence classes" ''J. Number Th.'' (to appear)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.A. Dias da Silva, Y.O. Hamidoune, "Cyclic subspaces of Grassmann derivations" ''Bull. London Math. Soc.'' , '''26''' (1994) pp. 140–146</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> P. Erdös, H. Heilbronn, "On the addition of residue classes mod <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110110/e11011027.png" />" ''Acta Arith.'' , '''9''' (1964) pp. 149–159</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> P. Erdös, R. Graham, "Old and new problems and results in combinatorial number theory" ''L'Enseign. Math.'' (1980) pp. 1–128</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> Y.O. Hamidoune, "The representation of some integers as a subset sum" ''Bull. London Math. Soc.'' , '''26''' (1994) pp. 557–563</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> H.B. Mann, "Addition theorems" , R.E. Krieger (1976) (Edition: Second)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N. Alon, "Subset sums" ''J. Number Th.'' , '''27''' (1987) pp. 196–205</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N. Alon, M.B. Nathanson, I. Z. Rusza, "The polynomial method and restricted sums of congruence classes" ''J. Number Th.'' (to appear)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.A. Dias da Silva, Y.O. Hamidoune, "Cyclic subspaces of Grassmann derivations" ''Bull. London Math. Soc.'' , '''26''' (1994) pp. 140–146</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> P. Erdös, H. Heilbronn, "On the addition of residue classes mod <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110110/e11011027.png" />" ''Acta Arith.'' , '''9''' (1964) pp. 149–159</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> P. Erdös, R. Graham, "Old and new problems and results in combinatorial number theory" ''L'Enseign. Math.'' (1980) pp. 1–128</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> Y.O. Hamidoune, "The representation of some integers as a subset sum" ''Bull. London Math. Soc.'' , '''26''' (1994) pp. 557–563</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> H.B. Mann, "Addition theorems" , R.E. Krieger (1976) (Edition: Second)</TD></TR></table> | ||
Revision as of 19:37, 5 June 2020
Let $ G $
be an Abelian group and let $ A \subset G $.
For $ k \in \mathbf N $,
let
$$ k \wedge A = \left \{ {\sum _ {x \in X } x } : {X \subset A \textrm{ and } \left | X \right | = k } \right \} . $$
(Here, $ | A | $ denotes the cardinality of a set $ A $.) Let $ p $ be a prime number and let $ A \subset \mathbf Z/p \mathbf Z $. It was conjectured by P. Erdös and H. Heilbronn that $ | {2 \wedge A } | \geq \min ( p,2 | A | - 3 ) $.
This conjecture, mentioned in [a5], was first proved in [a3], using linear algebra. As a consequence of the lower bound on the degree of the minimal polynomial of the Grasmann derivative, the following theorem is true [a3]: Let $ p $ be a prime number and let $ A \subset \mathbf Z/ {p \mathbf Z } $. Then
$$ \left | {k \wedge A } \right | \geq \min ( p,k ( \left | A \right | - k ) + 1 ) . $$
Applying this theorem with $ k = 2 $, one obtains the Erdös–Heilbronn conjecture mentioned above. A generalization of the theorem has been obtained in [a2]. Presently (1996), almost nothing is known for composite numbers. The following conjecture is proposed here: Let $ n $ be a composite number (cf. also Prime number) and let $ A \subset \mathbf Z/ {n \mathbf Z } $ be such that $ | A | \geq k - 1 + { {( n - 1 ) } / k } $. Then $ 0 \in j \wedge A $ for some $ 1 \leq j \leq k $.
For a prime number $ n $, the above conjecture is an easy consequence of the theorem above. Some applications to integer subset sums are contained in [a6]. Along the same lines, the conjecture has several implications. In particular, for $ k = 3 $ one finds: Let $ A \subset \{ 1 \dots n \} $ be such that $ | A | \geq 5 + { {( n - 1 ) } / 3 } $. Then there is a $ B \subset A $ such that $ 3 \leq | B | \leq 6 $ and $ \sum _ {x \in B } x = 2n $.
This was conjectured partially by Erdös and R. Graham [a5] and follows easily by applying the conjecture twice, after adding $ 0 $.
References
| [a1] | N. Alon, "Subset sums" J. Number Th. , 27 (1987) pp. 196–205 |
| [a2] | N. Alon, M.B. Nathanson, I. Z. Rusza, "The polynomial method and restricted sums of congruence classes" J. Number Th. (to appear) |
| [a3] | J.A. Dias da Silva, Y.O. Hamidoune, "Cyclic subspaces of Grassmann derivations" Bull. London Math. Soc. , 26 (1994) pp. 140–146 |
| [a4] | P. Erdös, H. Heilbronn, "On the addition of residue classes mod 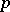 " Acta Arith. , 9 (1964) pp. 149–159 " Acta Arith. , 9 (1964) pp. 149–159 |
| [a5] | P. Erdös, R. Graham, "Old and new problems and results in combinatorial number theory" L'Enseign. Math. (1980) pp. 1–128 |
| [a6] | Y.O. Hamidoune, "The representation of some integers as a subset sum" Bull. London Math. Soc. , 26 (1994) pp. 557–563 |
| [a7] | H.B. Mann, "Addition theorems" , R.E. Krieger (1976) (Edition: Second) |
Erdös-Heilbronn problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Erd%C3%B6s-Heilbronn_problem&oldid=23260