Difference between revisions of "Character of a representation of an associative algebra"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | A | + | <!-- |
| + | c0215801.png | ||
| + | $#A+1 = 36 n = 1 | ||
| + | $#C+1 = 36 : ~/encyclopedia/old_files/data/C021/C.0201580 Character of a representation of an associative algebra | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | A function $ \phi $ | ||
| + | on the associative algebra $ A $ | ||
| + | defined by the formula $ \phi ( x) = \chi ( \pi ( x)) $ | ||
| + | for $ x \in A $, | ||
| + | where $ \pi $ | ||
| + | is a representation of $ A $ | ||
| + | and $ \chi $ | ||
| + | is a linear functional defined on some ideal $ I $ | ||
| + | in $ \pi ( A) $, | ||
| + | satisfying the condition $ \chi ( ab) = \chi ( ba) $ | ||
| + | for all $ a \in I $, | ||
| + | $ b \in \pi ( A) $. | ||
| + | If the representation $ \pi $ | ||
| + | is finite-dimensional or if the algebra $ \pi ( A) $ | ||
| + | contains a non-zero finite-dimensional operator, then for $ \chi $ | ||
| + | one usually considers the trace of the operator. Let $ A $ | ||
| + | be a $ C ^ {*} $- | ||
| + | algebra, $ \pi $ | ||
| + | a representation of the $ C ^ {*} $- | ||
| + | algebra $ A $ | ||
| + | such that the [[Von Neumann algebra|von Neumann algebra]] $ \mathfrak A $ | ||
| + | generated by $ \pi ( A) $ | ||
| + | is a [[Factor|factor]] of semi-finite type; let $ \chi ^ \prime $ | ||
| + | be a faithful normal semi-finite trace on $ \mathfrak A $ | ||
| + | and let $ \chi $ | ||
| + | be a linear extension of $ \chi ^ \prime $ | ||
| + | to an ideal $ \mathfrak M _ {\chi ^ \prime } $. | ||
| + | If the set $ \{ {x } : {x \in A, \chi ^ \prime ( \pi ( x)) < + \infty } \} $ | ||
| + | is non-zero, then the formula $ \phi ( x) = \chi ( \pi ( x)) $, | ||
| + | $ x \in A $, | ||
| + | determines a character of the representation of the algebra $ A $ | ||
| + | whose restriction to $ A ^ {+} $ | ||
| + | is a character of the $ C ^ {*} $- | ||
| + | algebra $ A $( | ||
| + | cf. [[Character of a C*-algebra|Character of a $ C ^ {*} $- | ||
| + | algebra]]). In many cases the character of a representation of an algebra determines the representation uniquely, up to a certain equivalence relation; for example, the character of an irreducible finite-dimensional representation determines the representation uniquely up to equivalence; the character of a factor representation of a $ C ^ {*} $- | ||
| + | algebra admitting a trace determines the representation uniquely up to quasi-equivalence. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Dixmier, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021580/c02158037.png" /> algebras" , North-Holland (1977) (Translated from French)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Dixmier, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021580/c02158037.png" /> algebras" , North-Holland (1977) (Translated from French)</TD></TR></table> | ||
Revision as of 16:43, 4 June 2020
A function $ \phi $
on the associative algebra $ A $
defined by the formula $ \phi ( x) = \chi ( \pi ( x)) $
for $ x \in A $,
where $ \pi $
is a representation of $ A $
and $ \chi $
is a linear functional defined on some ideal $ I $
in $ \pi ( A) $,
satisfying the condition $ \chi ( ab) = \chi ( ba) $
for all $ a \in I $,
$ b \in \pi ( A) $.
If the representation $ \pi $
is finite-dimensional or if the algebra $ \pi ( A) $
contains a non-zero finite-dimensional operator, then for $ \chi $
one usually considers the trace of the operator. Let $ A $
be a $ C ^ {*} $-
algebra, $ \pi $
a representation of the $ C ^ {*} $-
algebra $ A $
such that the von Neumann algebra $ \mathfrak A $
generated by $ \pi ( A) $
is a factor of semi-finite type; let $ \chi ^ \prime $
be a faithful normal semi-finite trace on $ \mathfrak A $
and let $ \chi $
be a linear extension of $ \chi ^ \prime $
to an ideal $ \mathfrak M _ {\chi ^ \prime } $.
If the set $ \{ {x } : {x \in A, \chi ^ \prime ( \pi ( x)) < + \infty } \} $
is non-zero, then the formula $ \phi ( x) = \chi ( \pi ( x)) $,
$ x \in A $,
determines a character of the representation of the algebra $ A $
whose restriction to $ A ^ {+} $
is a character of the $ C ^ {*} $-
algebra $ A $(
cf. Character of a $ C ^ {*} $-
algebra). In many cases the character of a representation of an algebra determines the representation uniquely, up to a certain equivalence relation; for example, the character of an irreducible finite-dimensional representation determines the representation uniquely up to equivalence; the character of a factor representation of a $ C ^ {*} $-
algebra admitting a trace determines the representation uniquely up to quasi-equivalence.
References
| [1] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [2] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) |
| [3] | J. Dixmier, "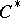 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
Character of a representation of an associative algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Character_of_a_representation_of_an_associative_algebra&oldid=19265