Difference between revisions of "Boundary correspondence, principle of"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | b0172701.png | ||
| + | $#A+1 = 20 n = 1 | ||
| + | $#C+1 = 20 : ~/encyclopedia/old_files/data/B017/B.0107270 Boundary correspondence, principle of | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| + | |||
| + | A principle formulated in the following way. One says that the principle of boundary correspondence holds for a mapping $ f $ | ||
| + | if the facts that $ f $ | ||
| + | is a continuous mapping of the closure $ \overline{G}\; $ | ||
| + | of a domain $ G $ | ||
| + | onto the closure $ \overline{D}\; $ | ||
| + | of a domain $ D $ | ||
| + | and $ f $ | ||
| + | is a homeomorphism of $ \overline{G}\; \setminus G $ | ||
| + | onto $ \overline{D}\; \setminus D $ | ||
| + | imply that $ f $ | ||
| + | is a topological mapping of $ \overline{G}\; $ | ||
| + | onto $ \overline{D}\; $. | ||
| + | Thus, the principle of boundary correspondence is in some sense converse to the boundary-correspondence principle (cf. [[Boundary correspondence (under conformal mapping)|Boundary correspondence (under conformal mapping)]]). | ||
| + | |||
| + | If $ G $ | ||
| + | and $ D $ | ||
| + | are plane domains with Euclidean boundaries homeomorphic to a circle and $ D $ | ||
| + | is bounded, then the principle of boundary correspondence holds for analytic functions $ f $ | ||
| + | on $ G $, | ||
| + | i.e. $ f $ | ||
| + | is a conformal mapping of $ G $ | ||
| + | onto $ D $. | ||
| + | In addition to that given above, various other forms of the principle of boundary correspondence are commonly used for conformal mappings (see [[#References|[1]]]). The principle of boundary correspondence has been verified for orientable mappings in Euclidean space (see [[#References|[2]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> M.A. Lavrent'ev, B.V. Shabat, "Methoden der komplexen Funktionentheorie" , Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.D. Kudryavtsev, "On differentiable mappings" ''Dokl. Akad. Nauk SSSR'' , '''95''' : 5 (1954) pp. 921–923 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.I. Pinchuk, "Holomorphic equivalence of certain classes of domains in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017270/b01727021.png" />" ''Math. USSR-Sb.'' , '''111 (153)''' : 1 (180) pp. 67–94; 159 ''Mat. Sb.'' , '''111 (153)''' : 1 (1980) pp. 67–94; 159</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M.A. Lavrent'ev, B.V. Shabat, "Methoden der komplexen Funktionentheorie" , Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.D. Kudryavtsev, "On differentiable mappings" ''Dokl. Akad. Nauk SSSR'' , '''95''' : 5 (1954) pp. 921–923 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.I. Pinchuk, "Holomorphic equivalence of certain classes of domains in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017270/b01727021.png" />" ''Math. USSR-Sb.'' , '''111 (153)''' : 1 (180) pp. 67–94; 159 ''Mat. Sb.'' , '''111 (153)''' : 1 (1980) pp. 67–94; 159</TD></TR></table> | ||
Revision as of 06:28, 30 May 2020
A principle formulated in the following way. One says that the principle of boundary correspondence holds for a mapping $ f $
if the facts that $ f $
is a continuous mapping of the closure $ \overline{G}\; $
of a domain $ G $
onto the closure $ \overline{D}\; $
of a domain $ D $
and $ f $
is a homeomorphism of $ \overline{G}\; \setminus G $
onto $ \overline{D}\; \setminus D $
imply that $ f $
is a topological mapping of $ \overline{G}\; $
onto $ \overline{D}\; $.
Thus, the principle of boundary correspondence is in some sense converse to the boundary-correspondence principle (cf. Boundary correspondence (under conformal mapping)).
If $ G $ and $ D $ are plane domains with Euclidean boundaries homeomorphic to a circle and $ D $ is bounded, then the principle of boundary correspondence holds for analytic functions $ f $ on $ G $, i.e. $ f $ is a conformal mapping of $ G $ onto $ D $. In addition to that given above, various other forms of the principle of boundary correspondence are commonly used for conformal mappings (see [1]). The principle of boundary correspondence has been verified for orientable mappings in Euclidean space (see [2]).
References
| [1] | M.A. Lavrent'ev, B.V. Shabat, "Methoden der komplexen Funktionentheorie" , Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian) |
| [2] | L.D. Kudryavtsev, "On differentiable mappings" Dokl. Akad. Nauk SSSR , 95 : 5 (1954) pp. 921–923 (In Russian) |
| [3] | S.I. Pinchuk, "Holomorphic equivalence of certain classes of domains in 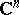 " Math. USSR-Sb. , 111 (153) : 1 (180) pp. 67–94; 159 Mat. Sb. , 111 (153) : 1 (1980) pp. 67–94; 159 " Math. USSR-Sb. , 111 (153) : 1 (180) pp. 67–94; 159 Mat. Sb. , 111 (153) : 1 (1980) pp. 67–94; 159 |
Boundary correspondence, principle of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boundary_correspondence,_principle_of&oldid=18233