Difference between revisions of "Aleksandrov compactification"
(Importing text file) |
(TeX done) |
||
| Line 1: | Line 1: | ||
''Aleksandrov compact extension'' | ''Aleksandrov compact extension'' | ||
| − | The unique Hausdorff [[ | + | The unique Hausdorff [[compactification]] $\alpha X$ of a locally compact, non-compact, Hausdorff space $X$, obtained by adding a single point $\infty$ to $X$. An arbitrary neighbourhood of the point $\infty$ must then have the form $\{\infty\} \cup (X \setminus F)$, where $F$ is a compact set in $X$. The Aleksandrov compactification $\alpha X$ is the smallest element in the set $B(X)$ of all compactifications of $X$. A smallest element in the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011260/a01126012.png" /> exists only for a locally compact space $B(X)$ and must coincide with $\alpha X$. |
| − | The Aleksandrov compactification was defined by P.S. Aleksandrov [[#References|[1]]] and plays an important role in topology. Thus, the Aleksandrov compactification | + | The Aleksandrov compactification was defined by P.S. Aleksandrov [[#References|[1]]] and plays an important role in topology. Thus, the Aleksandrov compactification $\alpha\mathbf{R}^n$ of the $n$-dimensional Euclidean space is identical with the $n$-dimensional sphere; the Aleksandrov compactification $\alpha\mathbf{N}$ of the set of natural numbers is homeomorphic to the space of a convergent sequence together with the limit point; the Aleksandrov compactification of the "open" [[Möbius strip]] coincides with the [[real projective plane]] $\mathbf{R}P^2$. There are pathological situations connected with the Aleksandrov compactification, e.g. there exists a perfectly-normal, locally compact and countably-compact space $X$ whose Aleksandrov compactification has the dimensions $\dim\alpha X < \dim X$ and $\mathrm{Ind}\,\alpha X < \mathrm{Ind}\,X$. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. [P.S. Aleksandrov] Aleksandroff, "Ueber die Metrisation der im Kleinen kompakten topologischen Räumen" ''Math. Ann.'' , '''92''' (1924) pp. 294–301</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. [P.S. Aleksandrov] Aleksandroff, "Ueber die Metrisation der im Kleinen kompakten topologischen Räumen" ''Math. Ann.'' , '''92''' (1924) pp. 294–301</TD></TR> | ||
| + | </table> | ||
| Line 14: | Line 16: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Dugundji, "Topology" , Allyn & Bacon (1966) (Theorem 8.4)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Dugundji, "Topology" , Allyn & Bacon (1966) (Theorem 8.4)</TD></TR> | ||
| + | </table> | ||
| + | |||
| + | {{TEX|done}} | ||
Revision as of 20:31, 10 January 2018
Aleksandrov compact extension
The unique Hausdorff compactification $\alpha X$ of a locally compact, non-compact, Hausdorff space $X$, obtained by adding a single point $\infty$ to $X$. An arbitrary neighbourhood of the point $\infty$ must then have the form $\{\infty\} \cup (X \setminus F)$, where $F$ is a compact set in $X$. The Aleksandrov compactification $\alpha X$ is the smallest element in the set $B(X)$ of all compactifications of $X$. A smallest element in the set 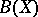 exists only for a locally compact space $B(X)$ and must coincide with $\alpha X$.
exists only for a locally compact space $B(X)$ and must coincide with $\alpha X$.
The Aleksandrov compactification was defined by P.S. Aleksandrov [1] and plays an important role in topology. Thus, the Aleksandrov compactification $\alpha\mathbf{R}^n$ of the $n$-dimensional Euclidean space is identical with the $n$-dimensional sphere; the Aleksandrov compactification $\alpha\mathbf{N}$ of the set of natural numbers is homeomorphic to the space of a convergent sequence together with the limit point; the Aleksandrov compactification of the "open" Möbius strip coincides with the real projective plane $\mathbf{R}P^2$. There are pathological situations connected with the Aleksandrov compactification, e.g. there exists a perfectly-normal, locally compact and countably-compact space $X$ whose Aleksandrov compactification has the dimensions $\dim\alpha X < \dim X$ and $\mathrm{Ind}\,\alpha X < \mathrm{Ind}\,X$.
References
| [1] | P.S. [P.S. Aleksandrov] Aleksandroff, "Ueber die Metrisation der im Kleinen kompakten topologischen Räumen" Math. Ann. , 92 (1924) pp. 294–301 |
Comments
The Aleksandrov compactification is also called the one-point compactification.
References
| [a1] | J. Dugundji, "Topology" , Allyn & Bacon (1966) (Theorem 8.4) |
Aleksandrov compactification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Aleksandrov_compactification&oldid=16469