Difference between revisions of "Dirichlet series"
(link to Dirichlet L-function) |
m (→References: expand bibliodata) |
||
| Line 132: | Line 132: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G.H. Hardy, M. Riesz, "The general theory of Dirichlet series" , Cambridge Univ. Press (1915)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> G.H. Hardy, M. Riesz, "The general theory of Dirichlet series" , Cambridge Univ. Press (1915) {{ZBL|45.0387.03}}</TD></TR> | ||
| + | </table> | ||
Revision as of 19:59, 7 January 2016
A series of the form
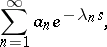 | (1) |
where the 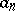 are complex coefficients,
are complex coefficients, 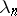 ,
, 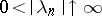 , are the exponents of the series, and
, are the exponents of the series, and 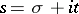 is a complex variable. If
is a complex variable. If 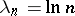 , one obtains the so-called ordinary Dirichlet series
, one obtains the so-called ordinary Dirichlet series
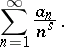 |
The series
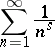 |
represents the Riemann zeta-function for  . The series
. The series
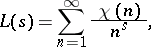 |
where 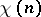 is a function, known as a Dirichlet character, were studied by P.G.L. Dirichlet (cf. Dirichlet
is a function, known as a Dirichlet character, were studied by P.G.L. Dirichlet (cf. Dirichlet 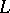 -function). Series (1) with arbitrary exponents
-function). Series (1) with arbitrary exponents 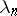 are known as general Dirichlet series.
are known as general Dirichlet series.
General Dirichlet series with positive exponents.
Let, initially, the 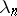 be positive numbers. The analogue of the Abel theorem for power series is then valid: If the series (1) converges at a point
be positive numbers. The analogue of the Abel theorem for power series is then valid: If the series (1) converges at a point 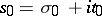 , it will converge in the half-plane
, it will converge in the half-plane 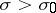 , and it will converge uniformly inside an arbitrary angle
, and it will converge uniformly inside an arbitrary angle 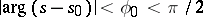 . The open domain of convergence of the series is some half-plane
. The open domain of convergence of the series is some half-plane 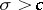 . The number
. The number  is said to be the abscissa of convergence of the Dirichlet series; the straight line
is said to be the abscissa of convergence of the Dirichlet series; the straight line 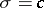 is said to be the axis of convergence of the series, and the half-plane
is said to be the axis of convergence of the series, and the half-plane 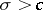 is said to be the half-plane of convergence of the series. As well as the half-plane of convergence one also considers the half-plane of absolute convergence of the Dirichlet series,
is said to be the half-plane of convergence of the series. As well as the half-plane of convergence one also considers the half-plane of absolute convergence of the Dirichlet series, 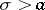 : The open domain in which the series converges absolutely (here
: The open domain in which the series converges absolutely (here  is the abscissa of absolute convergence). In general, the abscissas of convergence and of absolute convergence are different. But always:
is the abscissa of absolute convergence). In general, the abscissas of convergence and of absolute convergence are different. But always:
 |
and there exist Dirichlet series for which 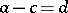 . If
. If 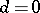 , the abscissa of convergence (abscissa of absolute convergence) is computed by the formula
, the abscissa of convergence (abscissa of absolute convergence) is computed by the formula
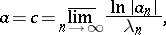 |
which is the analogue of the Cauchy–Hadamard formula. The case 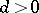 is more complicated: If the magnitude
is more complicated: If the magnitude
 |
is positive, then 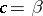 ; if
; if 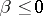 and the series (1) diverges at the point
and the series (1) diverges at the point 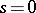 , then
, then 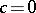 ; if
; if 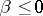 and the series (1) converges at the point
and the series (1) converges at the point  , then
, then
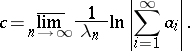 |
The sum of the series, 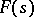 , is an analytic function in the half-plane of convergence. If
, is an analytic function in the half-plane of convergence. If  , the function
, the function 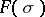 asymptotically behaves as the first term of the series,
asymptotically behaves as the first term of the series, 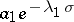 (if
(if 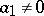 ). If the sum of the series is zero, then all coefficients of the series are zero. The maximal half-plane
). If the sum of the series is zero, then all coefficients of the series are zero. The maximal half-plane 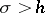 in which
in which 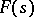 is an analytic function is said to be the half-plane of holomorphy of the function
is an analytic function is said to be the half-plane of holomorphy of the function 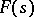 , the straight line
, the straight line 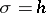 is known as the axis of holomorphy and the number
is known as the axis of holomorphy and the number 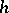 is called the abscissa of holomorphy. The inequality
is called the abscissa of holomorphy. The inequality 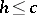 is true, and cases when
is true, and cases when  are possible. Let
are possible. Let 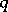 be the greatest lower bound of the numbers
be the greatest lower bound of the numbers 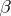 for which
for which 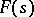 is bounded in modulus in the half-plane
is bounded in modulus in the half-plane 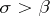 (
(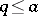 ). The formula
). The formula
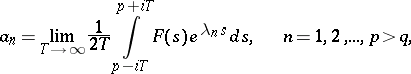 |
is valid, and entails the inequalities
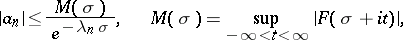 |
which are analogues of the Cauchy inequalities for the coefficients of a power series.
The sum of a Dirichlet series cannot be an arbitrary analytic function in some half-plane 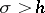 ; it must, for example, tend to zero if
; it must, for example, tend to zero if 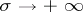 . However, the following holds: Whatever the analytic function
. However, the following holds: Whatever the analytic function 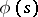 in the half-plane
in the half-plane 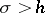 , it is possible to find a Dirichlet series (1) such that its sum
, it is possible to find a Dirichlet series (1) such that its sum 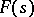 will differ from
will differ from 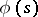 by an entire function.
by an entire function.
If the sequence of exponents has a density
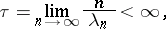 |
the difference between the abscissa of convergence (the abscissas of convergence and of absolute convergence coincide) and the abscissa of holomorphy does not exceed
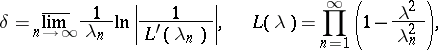 |
and there exist series for which this difference equals 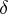 . The value of
. The value of 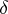 may be arbitrary in
may be arbitrary in 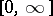 ; in particular, if
; in particular, if 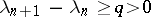 ,
, 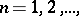 then
then 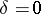 . The axis of holomorphy has the following property: On any of its segments of length
. The axis of holomorphy has the following property: On any of its segments of length 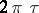 the sum of the series has at least one singular point.
the sum of the series has at least one singular point.
If the Dirichlet series (1) converges in the entire plane, its sum 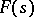 is an entire function. Let
is an entire function. Let
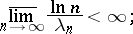 |
then the R-order of the entire function 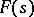 (Ritt order) is the magnitude
(Ritt order) is the magnitude
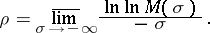 |
Its expression in terms of the coefficients of the series is
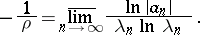 |
One can also introduce the concept of the R-type of a function 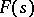 .
.
If
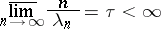 |
and if the function 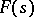 is bounded in modulus in a horizontal strip wider than
is bounded in modulus in a horizontal strip wider than 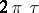 , then
, then 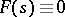 (the analogue of one of the Liouville theorems).
(the analogue of one of the Liouville theorems).
Dirichlet series with complex exponents.
For a Dirichlet series
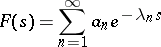 | (2) |
with complex exponents 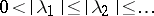 , the open domain of absolute convergence is convex. If
, the open domain of absolute convergence is convex. If
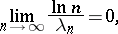 |
the open domains of convergence and absolute convergence coincide. The sum 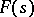 of the series (2) is an analytic function in the domain of convergence. The domain of holomorphy of
of the series (2) is an analytic function in the domain of convergence. The domain of holomorphy of 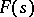 is, generally speaking, wider than the domain of convergence of the Dirichlet series (2). If
is, generally speaking, wider than the domain of convergence of the Dirichlet series (2). If
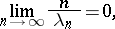 |
then the domain of holomorphy is convex.
Let
 |
let 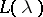 be an entire function of exponential type which has simple zeros at the points
be an entire function of exponential type which has simple zeros at the points 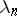 ,
, 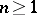 ; let
; let 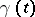 be the Borel-associated function to
be the Borel-associated function to 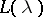 (cf. Borel transform); let
(cf. Borel transform); let 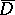 be the smallest closed convex set containing all the singular points of
be the smallest closed convex set containing all the singular points of 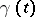 , and let
, and let
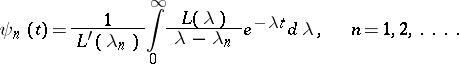 |
Then the functions 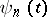 are regular outside
are regular outside 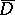 ,
, 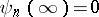 , and they are bi-orthogonal to the system
, and they are bi-orthogonal to the system 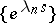 :
:
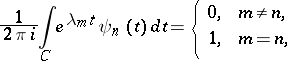 |
where 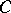 is a closed contour encircling
is a closed contour encircling 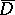 . If the functions
. If the functions 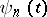 are continuous up to the boundary of
are continuous up to the boundary of 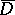 , the boundary
, the boundary 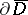 may be taken as
may be taken as  . To an arbitrary analytic function
. To an arbitrary analytic function 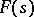 in
in 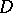 (the interior of the domain
(the interior of the domain 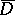 ) which is continuous in
) which is continuous in  one assigns a series:
one assigns a series:
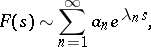 | (3) |
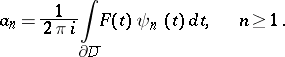 |
For a given bounded convex domain 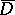 it is possible to construct an entire function
it is possible to construct an entire function 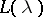 with simple zeros
with simple zeros 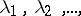 such that for any function
such that for any function 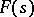 analytic in
analytic in 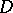 and continuous in
and continuous in 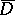 the series (3) converges uniformly inside
the series (3) converges uniformly inside 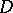 to
to 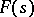 . For an analytic function
. For an analytic function 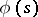 in
in 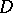 (not necessarily continuous in
(not necessarily continuous in  ) it is possible to find an entire function of exponential type zero,
) it is possible to find an entire function of exponential type zero,
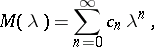 |
and a function 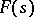 analytic in
analytic in  and continuous in
and continuous in 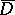 , such that
, such that
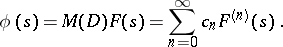 |
Then
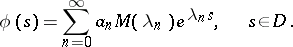 |
The representation of arbitrary analytic functions by Dirichlet series in a domain 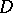 was also established in cases when
was also established in cases when 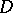 is the entire plane or an infinite convex polygonal domain (bounded by a finite number of rectilinear segments).
is the entire plane or an infinite convex polygonal domain (bounded by a finite number of rectilinear segments).
References
| [1] | A.F. Leont'ev, "Exponential series" , Moscow (1976) (In Russian) |
| [2] | S. Mandelbrojt, "Dirichlet series, principles and methods" , Reidel (1972) |
Comments
References
| [a1] | G.H. Hardy, M. Riesz, "The general theory of Dirichlet series" , Cambridge Univ. Press (1915) Zbl 45.0387.03 |
Dirichlet series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_series&oldid=36168