Difference between revisions of "Local field"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (link) |
||
| Line 5: | Line 5: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060130/l06013018.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060130/l06013018.png" /></td> </tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060130/l06013019.png" /> is the residue field and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060130/l06013020.png" /> is the field of fractions of a ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060130/l06013021.png" />. Moreover, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060130/l06013022.png" /> must be finite. There exists a structure theory for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060130/l06013023.png" />-dimensional local fields (see [[#References|[3]]]). | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060130/l06013019.png" /> is the residue field and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060130/l06013020.png" /> is the [[field of fractions]] of a ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060130/l06013021.png" />. Moreover, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060130/l06013022.png" /> must be finite. There exists a structure theory for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060130/l06013023.png" />-dimensional local fields (see [[#References|[3]]]). |
====References==== | ====References==== | ||
Revision as of 20:52, 28 November 2014
A field that is complete with respect to a discrete valuation and has finite residue field. The structure of a local field 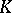 is well known: 1) if the characteristic of
is well known: 1) if the characteristic of 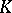 is
is  , then
, then 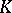 is a finite extension of the field
is a finite extension of the field 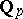 of
of 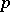 -adic numbers (cf.
-adic numbers (cf. 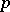 -adic number); 2) if the characteristic of
-adic number); 2) if the characteristic of 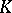 is greater than
is greater than  , then
, then 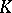 is isomorphic to the field
is isomorphic to the field 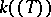 of formal power series over a finite field
of formal power series over a finite field 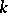 . Such fields are called local, in contrast to global fields (finite extensions of the fields
. Such fields are called local, in contrast to global fields (finite extensions of the fields 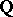 or
or 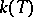 ), and are means for studying the latter. For cohomological properties of Galois extensions of local fields see [1], and also Adèle; Idèle; and Class field theory.
), and are means for studying the latter. For cohomological properties of Galois extensions of local fields see [1], and also Adèle; Idèle; and Class field theory.
To construct a class field theory of multi-dimensional schemes one uses a generalization of the concept of a local field. Namely, an  -dimensional local field is a sequence
-dimensional local field is a sequence 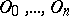 of complete discrete valuation rings together with isomorphisms
of complete discrete valuation rings together with isomorphisms
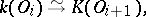 |
where 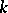 is the residue field and
is the residue field and 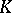 is the field of fractions of a ring
is the field of fractions of a ring 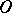 . Moreover,
. Moreover, 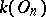 must be finite. There exists a structure theory for
must be finite. There exists a structure theory for  -dimensional local fields (see [3]).
-dimensional local fields (see [3]).
References
| [1] | J.-P. Serre, "Local fields" , Springer (1979) (Translated from French) MR0554237 Zbl 0423.12016 |
| [2] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) MR0911121 Zbl 0645.12001 Zbl 0153.07403 |
| [3] | A.N. Parshin, "Abelian coverings of arithmetic schemes" Soviet Math. Dokl. , 19 : 6 (1978) pp. 1438–1442 Dokl. Akad. Nauk SSSR , 243 (1978) pp. 855–858 MR0514485 Zbl 0443.12006 |
Comments
The concept of a local field is sometimes extended to include that of discretely valued fields with arbitrary residue fields. There is a class field theory for local fields with perfect residue fields in terms of a certain fundamental group [a1], [a2]. For an account of the class field theory of  -dimensional local fields (in terms of algebraic
-dimensional local fields (in terms of algebraic 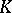 -theory) see also [a3]–[a5].
-theory) see also [a3]–[a5].
References
| [a1] | J.-P. Serre, "Sur les corps locaux à corps résiduel algébriquement clos" Bull. Soc. Math. France , 89 (1961) pp. 105–154 MR0142534 Zbl 0166.31103 |
| [a2] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , North-Holland (1971) pp. 648–674 ((Appendix: M. Hazewinkel, Classes de corps local)) MR1611211 MR0302656 MR0284446 Zbl 0223.14009 Zbl 0203.23401 Zbl 0134.16503 |
| [a3] | K. Kato, "Class field theory and algebraic 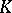 -theory" M. Raynaud (ed.) T. Shioda (ed.) , Algebraic geometry , Lect. notes in math. , 1016 , Springer (1983) pp. 109–126 -theory" M. Raynaud (ed.) T. Shioda (ed.) , Algebraic geometry , Lect. notes in math. , 1016 , Springer (1983) pp. 109–126 |
| [a4] | K. Kato, "Vanishing cycles, ramification of valuations and class field theory" Duke Math. J. , 55 (1987) pp. 629–661 MR0904945 Zbl 0665.14005 |
| [a5] | A.N. [A.N. Parshin] Paršin, "Local class field theory" Proc. Steklov Inst. Math. , 165 (1985) pp. 157–185 Trudy Mat. Inst. Steklov. , 165 (1984) pp. 143–170 |
Local field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Local_field&oldid=23888