Difference between revisions of "Linear summation method"
(TeX) |
(Category:Sequences, series, summability) |
||
| Line 1: | Line 1: | ||
{{TEX|done}} | {{TEX|done}} | ||
| − | A summation method (cf. [[ | + | A summation method (cf. [[Summation methods]]) having the properties of linearity: |
1) if the series $\sum_{k=0}^\infty a_k$ is summable by the summation method to the sum $A$, then the series $\sum_{k=0}^\infty ca_k$ is summable by this method to the sum $cA$; | 1) if the series $\sum_{k=0}^\infty a_k$ is summable by the summation method to the sum $A$, then the series $\sum_{k=0}^\infty ca_k$ is summable by this method to the sum $cA$; | ||
| Line 6: | Line 6: | ||
2) if the series $\sum_{k=0}^\infty a_k$, $\sum_{k=0}^\infty b_k$ are summable by the summation method to $A$ and $B$ respectively, then the series $\sum_{k=0}^\infty(a_k+b_k)$ is summable by this method to the sum $A+B$. | 2) if the series $\sum_{k=0}^\infty a_k$, $\sum_{k=0}^\infty b_k$ are summable by the summation method to $A$ and $B$ respectively, then the series $\sum_{k=0}^\infty(a_k+b_k)$ is summable by this method to the sum $A+B$. | ||
| − | All most widespread summation methods are linear; in particular, a [[ | + | All most widespread summation methods are linear; in particular, a [[matrix summation method]] and a [[semi-continuous summation method]]. There are non-linear summation methods. For example, the method in which summability of a series to the sum $S$ is defined by the existence of the limit $S$ of the sequence $\{T_n\}$, where |
$$T_n=\frac{s_{n+1}s_{n-1}-s_n^2}{s_{n+1}+s_{n-1}-2s_n}$$ | $$T_n=\frac{s_{n+1}s_{n-1}-s_n^2}{s_{n+1}+s_{n-1}-2s_n}$$ | ||
| Line 13: | Line 13: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.H. Hardy, "Divergent series" , Clarendon Press (1949)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G.F. Kangro, "Theory of summability of sequences and series" ''J. Soviet Math.'' , '''5''' (1976) pp. 1–45 ''Itogi Nauk. i Tekhn. Mat. Anal.'' , '''12''' (1974) pp. 5–70</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S.A. Baron, "Introduction to the theory of summability of series" , Tartu (1966) (In Russian)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> G.H. Hardy, "Divergent series" , Clarendon Press (1949)</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950)</TD></TR> | ||
| + | <TR><TD valign="top">[3]</TD> <TD valign="top"> G.F. Kangro, "Theory of summability of sequences and series" ''J. Soviet Math.'' , '''5''' (1976) pp. 1–45 ''Itogi Nauk. i Tekhn. Mat. Anal.'' , '''12''' (1974) pp. 5–70</TD></TR> | ||
| + | <TR><TD valign="top">[4]</TD> <TD valign="top"> S.A. Baron, "Introduction to the theory of summability of series" , Tartu (1966) (In Russian)</TD></TR> | ||
| + | </table> | ||
| + | |||
| + | [[Category:Sequences, series, summability]] | ||
Revision as of 20:04, 9 November 2014
A summation method (cf. Summation methods) having the properties of linearity:
1) if the series $\sum_{k=0}^\infty a_k$ is summable by the summation method to the sum $A$, then the series $\sum_{k=0}^\infty ca_k$ is summable by this method to the sum $cA$;
2) if the series $\sum_{k=0}^\infty a_k$, $\sum_{k=0}^\infty b_k$ are summable by the summation method to $A$ and $B$ respectively, then the series $\sum_{k=0}^\infty(a_k+b_k)$ is summable by this method to the sum $A+B$.
All most widespread summation methods are linear; in particular, a matrix summation method and a semi-continuous summation method. There are non-linear summation methods. For example, the method in which summability of a series to the sum $S$ is defined by the existence of the limit $S$ of the sequence $\{T_n\}$, where
$$T_n=\frac{s_{n+1}s_{n-1}-s_n^2}{s_{n+1}+s_{n-1}-2s_n}$$
(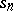 are the partial sums of the series), is not linear.
are the partial sums of the series), is not linear.
References
| [1] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [2] | R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950) |
| [3] | G.F. Kangro, "Theory of summability of sequences and series" J. Soviet Math. , 5 (1976) pp. 1–45 Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 5–70 |
| [4] | S.A. Baron, "Introduction to the theory of summability of series" , Tartu (1966) (In Russian) |
Linear summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_summation_method&oldid=33355