|
|
| Line 1: |
Line 1: |
| − | A group which has a normal series such that the order of every factor contains at most one prime from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p0710002.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p0710003.png" /> is a set of prime numbers). The class of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p0710004.png" />-separable groups contains the class of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p0710005.png" />-solvable groups (cf. [[Pi-solvable group|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p0710006.png" />-solvable group]]). For finite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p0710007.png" />-separable groups, the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p0710008.png" />-Sylow properties (cf. [[Sylow theorems|Sylow theorems]]) have been shown to hold (see [[#References|[1]]]). In fact, for any set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p0710009.png" />, a finite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100010.png" />-separable group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100011.png" /> contains a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100012.png" />-Hall subgroup (cf. also [[Hall subgroup|Hall subgroup]]), and any two <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100013.png" />-Hall subgroups are conjugate in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100014.png" />. Any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100015.png" />-subgroup of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100016.png" />-separable group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100017.png" /> is contained in some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100018.png" />-Hall subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100019.png" /> (see [[#References|[2]]]). | + | {{TEX|done}} |
| | + | A group which has a normal series such that the order of every factor contains at most one prime from $\pi$ ($\pi$ is a set of prime numbers). The class of $\pi$-separable groups contains the class of $\pi$-solvable groups (cf. [[Pi-solvable group|$\pi$-solvable group]]). For finite $\pi$-separable groups, the $\pi$-Sylow properties (cf. [[Sylow theorems|Sylow theorems]]) have been shown to hold (see [[#References|[1]]]). In fact, for any set $\pi_1\subseteq\pi$, a finite $\pi$-separable group $G$ contains a $\pi_1$-Hall subgroup (cf. also [[Hall subgroup|Hall subgroup]]), and any two $\pi_1$-Hall subgroups are conjugate in $G$. Any $\pi_1$-subgroup of a $\pi$-separable group $G$ is contained in some $\pi_1$-Hall subgroup of $G$ (see [[#References|[2]]]). |
| | | | |
| | ====References==== | | ====References==== |
| Line 7: |
Line 8: |
| | | | |
| | ====Comments==== | | ====Comments==== |
| − | Chunikhin's theorem says that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100021.png" /> is a divisor of the order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100022.png" /> of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100023.png" />-separable group such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100024.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100025.png" />, and if all prime divisors of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100026.png" /> are in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100027.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100028.png" /> has a subgroup of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100029.png" /> and all these subgroups are conjugate in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100030.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100031.png" /> consists of all prime numbers this becomes Hall's first theorem. | + | Chunikhin's theorem says that if $k$ is a divisor of the order $n$ of a $\pi$-separable group such that $n=kl$, $(k,l)=1$, and if all prime divisors of $k$ are in $\pi$, then $G$ has a subgroup of order $k$ and all these subgroups are conjugate in $G$. If $\pi$ consists of all prime numbers this becomes Hall's first theorem. |
| | | | |
| − | Gol'berg's theorem, [[#References|[a2]]], says that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100032.png" /> is a finite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100033.png" />-separable group and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100034.png" /> is a subset of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100035.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100036.png" /> has a Sylow <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100037.png" />-basis (cf. [[Sylow basis|Sylow basis]]) and all these bases are conjugate. | + | Gol'berg's theorem, [[#References|[a2]]], says that if $G$ is a finite $\pi$-separable group and $\pi_1$ is a subset of $\pi$, then $G$ has a Sylow $\pi_1$-basis (cf. [[Sylow basis|Sylow basis]]) and all these bases are conjugate. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.G. Kurosh, "The theory of groups" , '''2''' , Chelsea (1956) pp. 195ff (Translated from Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P.A. Gol'berg, "Sylow bases of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100038.png" />-separable groups" ''Dokl. Akad. Nauk SSSR'' , '''60''' (1949) pp. 615–618 (In Russian)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> S.A. Chunikhin, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071000/p07100039.png" />-properties of finite groups" ''Mat. Sb.'' , '''25''' (1949) pp. 321–346 (In Russian)</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.G. Kurosh, "The theory of groups" , '''2''' , Chelsea (1956) pp. 195ff (Translated from Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P.A. Gol'berg, "Sylow bases of $\pi$-separable groups" ''Dokl. Akad. Nauk SSSR'' , '''60''' (1949) pp. 615–618 (In Russian)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> S.A. Chunikhin, "On $\pi$-properties of finite groups" ''Mat. Sb.'' , '''25''' (1949) pp. 321–346 (In Russian)</TD></TR></table> |
Latest revision as of 09:33, 27 October 2014
A group which has a normal series such that the order of every factor contains at most one prime from $\pi$ ($\pi$ is a set of prime numbers). The class of $\pi$-separable groups contains the class of $\pi$-solvable groups (cf. $\pi$-solvable group). For finite $\pi$-separable groups, the $\pi$-Sylow properties (cf. Sylow theorems) have been shown to hold (see [1]). In fact, for any set $\pi_1\subseteq\pi$, a finite $\pi$-separable group $G$ contains a $\pi_1$-Hall subgroup (cf. also Hall subgroup), and any two $\pi_1$-Hall subgroups are conjugate in $G$. Any $\pi_1$-subgroup of a $\pi$-separable group $G$ is contained in some $\pi_1$-Hall subgroup of $G$ (see [2]).
References
| [1] | S.A. Chunikhin, "On 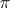 -separable groups" Dokl. Akad. Nauk SSSR , 59 : 3 (1948) pp. 443–445 (In Russian) -separable groups" Dokl. Akad. Nauk SSSR , 59 : 3 (1948) pp. 443–445 (In Russian) |
| [2] | P. Hall, "Theorems like Sylow's" Proc. London Math. Soc. , 6 : 22 (1956) pp. 286–304 |
Chunikhin's theorem says that if $k$ is a divisor of the order $n$ of a $\pi$-separable group such that $n=kl$, $(k,l)=1$, and if all prime divisors of $k$ are in $\pi$, then $G$ has a subgroup of order $k$ and all these subgroups are conjugate in $G$. If $\pi$ consists of all prime numbers this becomes Hall's first theorem.
Gol'berg's theorem, [a2], says that if $G$ is a finite $\pi$-separable group and $\pi_1$ is a subset of $\pi$, then $G$ has a Sylow $\pi_1$-basis (cf. Sylow basis) and all these bases are conjugate.
References
| [a1] | A.G. Kurosh, "The theory of groups" , 2 , Chelsea (1956) pp. 195ff (Translated from Russian) |
| [a2] | P.A. Gol'berg, "Sylow bases of $\pi$-separable groups" Dokl. Akad. Nauk SSSR , 60 (1949) pp. 615–618 (In Russian) |
| [a3] | S.A. Chunikhin, "On $\pi$-properties of finite groups" Mat. Sb. , 25 (1949) pp. 321–346 (In Russian) |
How to Cite This Entry:
Pi-separable group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pi-separable_group&oldid=13312
This article was adapted from an original article by S.P. Strunkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article -separable groups" Dokl. Akad. Nauk SSSR , 59 : 3 (1948) pp. 443–445 (In Russian)
-separable groups" Dokl. Akad. Nauk SSSR , 59 : 3 (1948) pp. 443–445 (In Russian)