Difference between revisions of "Interval and segment"
(Importing text file) |
(Category:Order, lattices, ordered algebraic structures) |
||
| Line 5: | Line 5: | ||
''BSE-3'' | ''BSE-3'' | ||
| − | The notion of an interval in a partially ordered set is more general. An interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052090/i05209025.png" /> consists in this setting of all elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052090/i05209026.png" /> of the | + | The notion of an interval in a [[partially ordered set]] is more general. An interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052090/i05209025.png" /> consists in this setting of all elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052090/i05209026.png" /> of the partially ordered set that satisfy <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052090/i05209027.png" />. An interval in a partially ordered set that consists of precisely two elements is called a ''simple'' or an ''[[elementary interval]]''. |
''L.A. Skornyakov'' | ''L.A. Skornyakov'' | ||
| Line 11: | Line 11: | ||
====Comments==== | ====Comments==== | ||
In English the term "segment" is not often used, except in specifically geometrical contexts; the normal terms are "open interval" and "closed interval" , cf. also [[Interval, open|Interval, open]]; [[Interval, closed|Interval, closed]]. | In English the term "segment" is not often used, except in specifically geometrical contexts; the normal terms are "open interval" and "closed interval" , cf. also [[Interval, open|Interval, open]]; [[Interval, closed|Interval, closed]]. | ||
| + | |||
| + | [[Category:Order, lattices, ordered algebraic structures]] | ||
Revision as of 22:02, 12 October 2014
The simplest sets of points on the line. An interval (open interval) is a set of points on a line lying between two fixed points  and
and  , where
, where  and
and  themselves are considered not to belong to the interval. A segment (closed interval) is a set of points between two points
themselves are considered not to belong to the interval. A segment (closed interval) is a set of points between two points  and
and  , where
, where  and
and  are included. The terms "interval" and "segment" are also used for the corresponding sets of real numbers: an interval consists of numbers
are included. The terms "interval" and "segment" are also used for the corresponding sets of real numbers: an interval consists of numbers  satisfying
satisfying 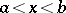 , while a segment consists of those
, while a segment consists of those  for which
for which 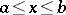 . An interval is denoted by
. An interval is denoted by 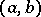 , or
, or  , and a segment by
, and a segment by 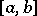 .
.
The term "interval" is also used in a wider sense for arbitrary connected sets on the line. In this case one considers not only 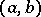 but also the infinite, or improper, intervals
but also the infinite, or improper, intervals 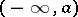 ,
, 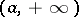 ,
, 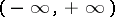 , the segment
, the segment 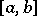 , and the half-open intervals
, and the half-open intervals 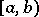 ,
, 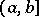 ,
, 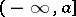 ,
,  . Here, a round bracket indicates that the appropriate end of the interval is not included, while a square bracket indicates that the end is included.
. Here, a round bracket indicates that the appropriate end of the interval is not included, while a square bracket indicates that the end is included.
BSE-3
The notion of an interval in a partially ordered set is more general. An interval 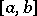 consists in this setting of all elements
consists in this setting of all elements  of the partially ordered set that satisfy
of the partially ordered set that satisfy 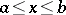 . An interval in a partially ordered set that consists of precisely two elements is called a simple or an elementary interval.
. An interval in a partially ordered set that consists of precisely two elements is called a simple or an elementary interval.
L.A. Skornyakov
Comments
In English the term "segment" is not often used, except in specifically geometrical contexts; the normal terms are "open interval" and "closed interval" , cf. also Interval, open; Interval, closed.
Interval and segment. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Interval_and_segment&oldid=14087