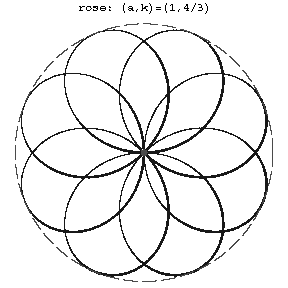|
|
| Line 1: |
Line 1: |
| | + | {{TEX|done}} |
| | Planar curves whose equations in polar coordinates have the form | | Planar curves whose equations in polar coordinates have the form |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r0826101.png" /></td> </tr></table>
| + | $$\rho=a\sin k\phi,$$ |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r0826102.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r0826103.png" /> are constants. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r0826104.png" /> is a rational number, then a rose is an [[Algebraic curve|algebraic curve]] of even order. | + | where $a$ and $k$ are constants. If $k=m/n$ is a rational number, then a rose is an [[Algebraic curve|algebraic curve]] of even order. |
| | | | |
| | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r082610a.gif" /> | | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r082610a.gif" /> |
| Line 9: |
Line 10: |
| | Figure: r082610a | | Figure: r082610a |
| | | | |
| − | The order of a rose is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r0826105.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r0826106.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r0826107.png" /> are odd, and to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r0826108.png" /> if either <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r0826109.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261010.png" /> is even. The entire curve is situated inside the circle of radius <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261011.png" /> and consists of congruent parts, called petals (see Fig.). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261012.png" /> is an integer, then the rose consists of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261013.png" /> petals for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261014.png" /> odd and of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261015.png" /> petals for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261016.png" /> even. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261017.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261018.png" /> are relatively prime, then the rose consists of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261019.png" /> petals for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261020.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261021.png" /> odd, and of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261022.png" /> petals when either <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261023.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261024.png" /> is even. | + | The order of a rose is equal to $m+n$ if $m$ and $n$ are odd, and to $2(m+n)$ if either $m$ or $n$ is even. The entire curve is situated inside the circle of radius $a$ and consists of congruent parts, called petals (see Fig.). If $k$ is an integer, then the rose consists of $k$ petals for $k$ odd and of $2k$ petals for $k$ even. If $k=m/n$ and $m,n$ are relatively prime, then the rose consists of $m$ petals for $m$ and $n$ odd, and of $2m$ petals when either $m$ or $n$ is even. |
| | | | |
| − | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261025.png" /> is irrational there are infinitely many petals. Roses belong to the family of cycloidal curves (cf. [[Cycloidal curve|Cycloidal curve]]). They are hypocycloids if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261026.png" />, and epicycloids if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261027.png" />. | + | When $k$ is irrational there are infinitely many petals. Roses belong to the family of cycloidal curves (cf. [[Cycloidal curve|Cycloidal curve]]). They are hypocycloids if $k>1$, and epicycloids if $k<1$. |
| | | | |
| | Roses are also related to the family of cycloidal curves by the fact that they are pedals of epi- and hypocycloids with respect to the centre of their fixed circle. | | Roses are also related to the family of cycloidal curves by the fact that they are pedals of epi- and hypocycloids with respect to the centre of their fixed circle. |
| | | | |
| − | The arc length of a rose is given by an elliptic integral of the second kind. The area of one petal is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082610/r08261028.png" />. | + | The arc length of a rose is given by an elliptic integral of the second kind. The area of one petal is $S=\pi a^2/4k$. |
| | | | |
| | Roses are also called curves of Guido Grandi, who was the first to describe them in 1728. | | Roses are also called curves of Guido Grandi, who was the first to describe them in 1728. |
Latest revision as of 18:58, 16 April 2014
Planar curves whose equations in polar coordinates have the form
$$\rho=a\sin k\phi,$$
where $a$ and $k$ are constants. If $k=m/n$ is a rational number, then a rose is an algebraic curve of even order.
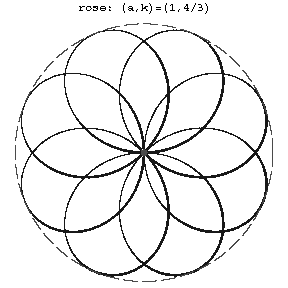
Figure: r082610a
The order of a rose is equal to $m+n$ if $m$ and $n$ are odd, and to $2(m+n)$ if either $m$ or $n$ is even. The entire curve is situated inside the circle of radius $a$ and consists of congruent parts, called petals (see Fig.). If $k$ is an integer, then the rose consists of $k$ petals for $k$ odd and of $2k$ petals for $k$ even. If $k=m/n$ and $m,n$ are relatively prime, then the rose consists of $m$ petals for $m$ and $n$ odd, and of $2m$ petals when either $m$ or $n$ is even.
When $k$ is irrational there are infinitely many petals. Roses belong to the family of cycloidal curves (cf. Cycloidal curve). They are hypocycloids if $k>1$, and epicycloids if $k<1$.
Roses are also related to the family of cycloidal curves by the fact that they are pedals of epi- and hypocycloids with respect to the centre of their fixed circle.
The arc length of a rose is given by an elliptic integral of the second kind. The area of one petal is $S=\pi a^2/4k$.
Roses are also called curves of Guido Grandi, who was the first to describe them in 1728.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
These curves are also called rhodoneas, cf. [a1].
References
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
| [a2] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
How to Cite This Entry:
Roses (curves). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Roses_(curves)&oldid=16994
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article