Difference between revisions of "Galois geometry"
Justinwsmith (talk | contribs) (replacing some image tags by latex -- formatting of article sources is sorely needed.) |
m (Added category TEXdone) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
Briefly speaking, Galois geometry is analytical and algebraic geometry over a [[Galois field|Galois field]], that is, geometry over a [[Finite field|finite field]] (cf. also [[Analytic geometry|Analytic geometry]]; [[Algebraic geometry|Algebraic geometry]]). Its beginning may be traced back to a result of B. Segre (1954), saying that every $(q+1)$-arc, i.e. set of $q+1$ three-by-three non-collinear points, of a projective Galois plane $PG(2, q), q = p^h, p$ an odd prime number, is an irreducible [[Conic|conic]] [[#References|[a7]]]. | Briefly speaking, Galois geometry is analytical and algebraic geometry over a [[Galois field|Galois field]], that is, geometry over a [[Finite field|finite field]] (cf. also [[Analytic geometry|Analytic geometry]]; [[Algebraic geometry|Algebraic geometry]]). Its beginning may be traced back to a result of B. Segre (1954), saying that every $(q+1)$-arc, i.e. set of $q+1$ three-by-three non-collinear points, of a projective Galois plane $PG(2, q), q = p^h, p$ an odd prime number, is an irreducible [[Conic|conic]] [[#References|[a7]]]. | ||
Revision as of 12:58, 12 December 2013
Briefly speaking, Galois geometry is analytical and algebraic geometry over a Galois field, that is, geometry over a finite field (cf. also Analytic geometry; Algebraic geometry). Its beginning may be traced back to a result of B. Segre (1954), saying that every $(q+1)$-arc, i.e. set of $q+1$ three-by-three non-collinear points, of a projective Galois plane $PG(2, q), q = p^h, p$ an odd prime number, is an irreducible conic [a7].
The connections between Galois geometry and other branches of mathematics are numerous: classical algebraic geometry and algebra [a18], information theory [a11], physics [a14], coding theory (cf. also Coding and decoding) [a12], cryptography [a17] and mathematical statistics [a11], [a13].
There are graphic characterizations of remarkable algebraic varieties [a15] like quadrics [a10], Veronese varieties, Grassmann varieties, unitals [a8], etc. (cf. also Algebraic variety). Further, there are links between caps and codes [a12], [a13] (cf. also Goppa code), with the classification of $k$-sets from the point of view of characters [a9], and with the study of ovals and hyperovals, the theory of spreads and blocking sets and the theory of combinatorial designs [a16] (cf. also Block design).
General references are: [a1], [a2], [a3], [a4], [a5], [a6]. The other references deal with specific topics related with Galois geometry.
References
| [a1] | T. Beth, D. Jungnickel, H. Lenz, "Design theory" , BI Wissenschaftsverlag & Cambridge Univ. Press (1984) MR1742365 MR1729456 MR0890103 MR0779284 Zbl 0945.05005 Zbl 0945.05004 Zbl 0602.05001 Zbl 0569.05002 |
| [a2] | J.W.P. Hirschfeld, "Projective geometries over finite fields" , Oxford Univ. Press (1979) MR0554919 Zbl 0418.51002 |
| [a3] | J.W.P. Hirschfeld, "Finite projective spaces in three dimensions" , Oxford Univ. Press (1985) MR840877 |
| [a4] | J.W.P. Hirschfeld, J.A. Thas, "General Galois geometries" , Oxford Sci. Publ. , Clarendon Press (1991) MR1363259 Zbl 0789.51001 |
| [a5] | B. Segre, "Introduction to Galois geometries" J.W.P. Hirschfeld (ed.) Atti Accad. Naz. Lincei, Mem. , 8 (1967) pp. 133–236 MR0238846 Zbl 0194.21503 |
| [a6] | M. Scafati, G. Tallini, "Geometrie di Galois e teoria dei codici" , CISU , Roma (1995) |
| [a7] | B. Segre, "Ovals in a finite projective plane" Canad. J. Math. , 7 (1955) pp. 414–416 MR0071034 Zbl 0065.13402 |
| [a8] | M. Scafati Tallini, "Caratterizzazione grafica delle forme hermitiane di un 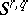 " Rend. Mat. Roma , 26 (1967) pp. 273–303 Zbl 0162.24201 " Rend. Mat. Roma , 26 (1967) pp. 273–303 Zbl 0162.24201 |
| [a9] | M. Scafati Tallini, "On 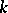 -sets of kind -sets of kind 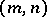 of a finite projective or affine space" Ann. Discrete Math. , 14 (1982) pp. 39–56 of a finite projective or affine space" Ann. Discrete Math. , 14 (1982) pp. 39–56 |
| [a10] | G. Tallini, "Sulle 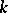 -calotte di uno spazio lineare finito" Ann. di Mat. (4) , 42 (1956) pp. 119–164 MR85531 -calotte di uno spazio lineare finito" Ann. di Mat. (4) , 42 (1956) pp. 119–164 MR85531 |
| [a11] | G. Tallini, "Le geometrie di Galois e le loro applicazioni alla statistica e alla teoria dell'informazione" Rend. Mat. Roma , 19 (1960) pp. 379–400 MR0125484 Zbl 0211.51403 |
| [a12] | G. Tallini, "On caps of kind  in a Galois in a Galois  -dimensional space" Acta Arithmetica , VII (1961) pp. 19–28 MR150647 -dimensional space" Acta Arithmetica , VII (1961) pp. 19–28 MR150647 |
| [a13] | G. Tallini, "Un'applicazione delle geometrie di Galois a questioni di statistica" Rend. Accad. Naz. Lincei , 8 (1963) pp. 479–485 MR0167432 |
| [a14] | G. Tallini, "Geometrie di Galois e loro applicazioni alla fisica" , Lecture Notes Sem. Lab. Naz. CNEN , F–70–63 (1970) |
| [a15] | G. Tallini, "Graphic characterization of algebraic varieties in Galois space" , Atti Conv. Int. Teorie Combinatorie , II , Accad. Naz. Lincei (1976) pp. 153–165 MR462986 Zbl 0364.50010 |
| [a16] | G. Tallini, "Lectures on Galois geometries and Steiner systems" , Geometries, Codes and Cryptography: CISM courses and lectures , 313 , Springer (1990) pp. 1–23 MR1140926 Zbl 0714.51002 |
| [a17] | G. Tallini, A. Beutelspacher, "Examples of essentially  -fold secure geometric authentication systems with large -fold secure geometric authentication systems with large  " Rend. Mat. Roma (VII) , 10 (1990) pp. 321–326 MR1076161 " Rend. Mat. Roma (VII) , 10 (1990) pp. 321–326 MR1076161 |
| [a18] | G. Tallini, "General multivalued algebraic structures and geometric spaces" , Proc. 4th Int. Congress on Algebraic Hyperstructures and Applications, Xanthi, Greece (1990) pp. 197–202 MR1125331 |
Galois geometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Galois_geometry&oldid=27488