Difference between revisions of "Satake compactification"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 11: | Line 11: | ||
Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004015.png" /> is taken to be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004016.png" />. It is a compact Riemann surface (thus automatically an [[Algebraic curve|algebraic curve]]). An important ingredient, both here and in Satake's generalization, is reduction theory. Relative to the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004017.png" />, it asserts that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004019.png" /> satisfy <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004020.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004021.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004022.png" /> lies in the group of real translations (equivalently, in the parabolic group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004023.png" /> of upper-triangular matrices, which is the stabilizer of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004024.png" />). This gives an embedding of the punctured disc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004025.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004026.png" />, and one is inserting the missing origin by adjoining <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004027.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004028.png" />. | Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004015.png" /> is taken to be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004016.png" />. It is a compact Riemann surface (thus automatically an [[Algebraic curve|algebraic curve]]). An important ingredient, both here and in Satake's generalization, is reduction theory. Relative to the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004017.png" />, it asserts that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004019.png" /> satisfy <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004020.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004021.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004022.png" /> lies in the group of real translations (equivalently, in the parabolic group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004023.png" /> of upper-triangular matrices, which is the stabilizer of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004024.png" />). This gives an embedding of the punctured disc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004025.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004026.png" />, and one is inserting the missing origin by adjoining <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004027.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004028.png" />. | ||
| − | There was great interest in doing something similar for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004029.png" />, the moduli space of Abelian varieties (cf. also [[Moduli theory|Moduli theory]]; [[Abelian variety|Abelian variety]]), which is the quotient <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004030.png" />; here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004031.png" /> is the Siegel upper half-space of genus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004032.png" />, which is the symmetric space for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004033.png" />, the rank-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004034.png" /> group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004035.png" /> symplectic matrices. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004036.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004037.png" /> (from the preceding paragraph). Satake first observed, in [[#References|[a9]]], that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004038.png" /> could be topologized in a way that makes it a compact space with | + | There was great interest in doing something similar for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004029.png" />, the moduli space of Abelian varieties (cf. also [[Moduli theory|Moduli theory]]; [[Abelian variety|Abelian variety]]), which is the quotient <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004030.png" />; here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004031.png" /> is the Siegel upper half-space of genus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004032.png" />, which is the symmetric space for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004033.png" />, the rank-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004034.png" /> group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004035.png" /> symplectic matrices. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004036.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004037.png" /> (from the preceding paragraph). Satake first observed, in [[#References|[a9]]], that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004038.png" /> could be topologized in a way that makes it a compact space with "hereditary" structure: the closure of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004039.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004040.png" /> is homeomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004041.png" />. Some refer to this space as "the" Satake compactification of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004042.png" />. |
Satake compactifications, in the sense of [[#References|[a13]]] (after [[#References|[a11]]] and [[#References|[a3]]]), are defined from the following setting [[#References|[a10]]]. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004043.png" /> be the symmetric space of non-compact type for the real semi-simple Lie group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004044.png" /> (cf. also [[Lie group, semi-simple|Lie group, semi-simple]]). Each faithful finite-dimensional representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004045.png" /> (cf. also [[Representation of a Lie algebra|Representation of a Lie algebra]]) determines an embedding of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004046.png" /> in some real projective space, so let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004047.png" /> be the closure of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004048.png" />. The boundary of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004049.png" /> consists of pieces, called boundary components, that are homogeneous under a class of parabolic subgroups of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004050.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004051.png" /> is the (real) rank of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004052.png" />, there are only <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004053.png" /> distinct such spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004054.png" /> up to homeomorphism, corresponding to the non-empty subsets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004055.png" /> of a set of simple roots, and as such they form a semi-lattice; if one then writes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004056.png" />, the identity mapping of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004057.png" /> extends to a continuous mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004058.png" /> whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004059.png" />. | Satake compactifications, in the sense of [[#References|[a13]]] (after [[#References|[a11]]] and [[#References|[a3]]]), are defined from the following setting [[#References|[a10]]]. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004043.png" /> be the symmetric space of non-compact type for the real semi-simple Lie group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004044.png" /> (cf. also [[Lie group, semi-simple|Lie group, semi-simple]]). Each faithful finite-dimensional representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004045.png" /> (cf. also [[Representation of a Lie algebra|Representation of a Lie algebra]]) determines an embedding of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004046.png" /> in some real projective space, so let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004047.png" /> be the closure of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004048.png" />. The boundary of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004049.png" /> consists of pieces, called boundary components, that are homogeneous under a class of parabolic subgroups of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004050.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004051.png" /> is the (real) rank of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004052.png" />, there are only <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004053.png" /> distinct such spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004054.png" /> up to homeomorphism, corresponding to the non-empty subsets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004055.png" /> of a set of simple roots, and as such they form a semi-lattice; if one then writes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004056.png" />, the identity mapping of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004057.png" /> extends to a continuous mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004058.png" /> whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004059.png" />. | ||
| Line 17: | Line 17: | ||
When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004060.png" /> is the real [[Lie group|Lie group]] associated to an [[Algebraic group|algebraic group]] defined over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004061.png" />, a boundary component is said to be rational when its normalizing [[Parabolic subgroup|parabolic subgroup]] is defined over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004062.png" />. Likewise, the structure over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004063.png" /> determines the class of arithmetic subgroups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004064.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004065.png" />. Take <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004066.png" /> to be the union of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004067.png" /> and its rational boundary components. Then, with a suitable topology on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004068.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004069.png" /> is, under mild hypotheses, a compactification of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004070.png" />. The collection of these inherit the semi-lattice structure from the above. There is a precise sense in which the topology of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004071.png" /> is induced from that of the closure of a Siegel set in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004072.png" />. | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004060.png" /> is the real [[Lie group|Lie group]] associated to an [[Algebraic group|algebraic group]] defined over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004061.png" />, a boundary component is said to be rational when its normalizing [[Parabolic subgroup|parabolic subgroup]] is defined over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004062.png" />. Likewise, the structure over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004063.png" /> determines the class of arithmetic subgroups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004064.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004065.png" />. Take <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004066.png" /> to be the union of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004067.png" /> and its rational boundary components. Then, with a suitable topology on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004068.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004069.png" /> is, under mild hypotheses, a compactification of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004070.png" />. The collection of these inherit the semi-lattice structure from the above. There is a precise sense in which the topology of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004071.png" /> is induced from that of the closure of a Siegel set in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004072.png" />. | ||
| − | The [[Baily–Borel compactification|Baily–Borel compactification]] is one of the minimal Satake compactifications in the case where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004073.png" /> is Hermitian, i.e., has a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004074.png" />-invariant complex structure (cf. also [[Hermitian symmetric space|Hermitian symmetric space]]). This includes the case of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004075.png" /> above. Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004076.png" /> gets embedded as a bounded symmetric domain. By means of automorphic forms of sufficiently high weight, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004077.png" /> gets embedded as a normal algebraic subvariety of complex projective space [[#References|[a2]]]. This fact has rather strong consequences, for the singular locus of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004078.png" /> has | + | The [[Baily–Borel compactification|Baily–Borel compactification]] is one of the minimal Satake compactifications in the case where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004073.png" /> is Hermitian, i.e., has a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004074.png" />-invariant complex structure (cf. also [[Hermitian symmetric space|Hermitian symmetric space]]). This includes the case of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004075.png" /> above. Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004076.png" /> gets embedded as a bounded symmetric domain. By means of automorphic forms of sufficiently high weight, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004077.png" /> gets embedded as a normal algebraic subvariety of complex projective space [[#References|[a2]]]. This fact has rather strong consequences, for the singular locus of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004078.png" /> has "high" codimension in general, and one can invoke general results from [[Algebraic geometry|algebraic geometry]]. It implies the existence of big families of Abelian varieties that do not degenerate. This compactification also enters into the topological interpretation of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004080.png" />-cohomology of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004081.png" />, as conjectured in [[#References|[a12]]] and proved by E. Looijenga, and L. Saper and M. Stern. |
| − | The applications of Satake compactifications cover a range of other areas. The stable cohomology of | + | The applications of Satake compactifications cover a range of other areas. The stable cohomology of "the" Satake compactification was determined by R. Charney and R. Lee [[#References|[a5]]] for application in [[K-theory|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004082.png" />-theory]]. Non-Hermitian Satake compactifications occur in the combinatorial data of the toroidal compactifications of [[#References|[a1]]] (see [[#References|[a8]]], § 2), which provide resolution of the singularities of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004083.png" /> (cf. also [[Resolution of singularities|Resolution of singularities]]). |
Another compactification, the reductive Borel–Serre, a simple quotient of the manifold-with-corners constructed in [[#References|[a4]]] (see, e.g., [[#References|[a7]]]), dominates all Satake compactifications, and often coincides with the unique maximal one. It has played an increasing role in the theory of automorphic forms. It is the natural place to study the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004085.png" />-cohomology [[#References|[a12]]] and to define weighted cohomology [[#References|[a6]]]. | Another compactification, the reductive Borel–Serre, a simple quotient of the manifold-with-corners constructed in [[#References|[a4]]] (see, e.g., [[#References|[a7]]]), dominates all Satake compactifications, and often coincides with the unique maximal one. It has played an increasing role in the theory of automorphic forms. It is the natural place to study the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004085.png" />-cohomology [[#References|[a12]]] and to define weighted cohomology [[#References|[a6]]]. | ||
| Line 26: | Line 26: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Ash, D. Mumford, M. Rapoport, Y.-S. Tai, "Smooth compactification of locally symmetric varieties" , Math. Sci. Press (1975) {{MR|0457437}} {{ZBL|0334.14007}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Baily, A. Borel, "Compactification of quotients of bounded symmetric domains" ''Ann. of Math.'' , '''84''' (1966) pp. 442–528 {{MR|216035}} {{ZBL|0154.08602}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Borel, "Ensembles fondamentaux pour les groupes arithmétiques" ''Colloq. Théorie de Groupes Algébriques, Bruxelles'' (1962) pp. 23–40 {{MR|0148666}} {{ZBL|0161.02603}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A. Borel, J.-P. Serre, "Corners and arithmetic groups" ''Comment. Math. Helv.'' , '''48''' (1973) pp. 436–491 {{MR|0387495}} {{ZBL|0274.22011}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> R. Charney, R. Lee, "Cohomology of the Satake compactification" ''Topology'' , '''22''' (1983) pp. 389–423 {{MR|0715247}} {{ZBL|0562.32017}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> M. Goresky, G. Harder, R. MacPherson, "Weighted cohomology" ''Invent. Math.'' , '''116''' (1994) pp. 139–213 {{MR|1253192}} {{ZBL|0849.11047}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> M. Goresky, Y.-S. Tai, "Toroidal and reductive Borel–Serre compactifications of locally symmetric spaces" ''Amer. J. Math.'' , '''121''' (1999) pp. 1095–1151 {{MR|1712965}} {{ZBL|1008.32014}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> M. Harris, S. Zucker, "Boundary cohomology of Shimura varieties, II: Hodge theory at the boundary" ''Invent. Math.'' , '''116''' (1994) pp. 243–307 {{MR|1253194}} {{ZBL|0860.11031}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> I. Satake, "On the compactification of the Siegel space" ''J. Indian Math. Soc.'' , '''20''' (1956) pp. 259–281 {{MR|0084842}} {{ZBL|0072.30002}} </TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> I. Satake, "On representations and compactifications of symmetric Riemannian spaces." ''Ann. of Math.'' , '''71''' (1960) pp. 77–110 {{MR|0118775}} {{ZBL|0094.34603}} </TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> I. Satake, "On compactifications of the quotient spaces for arithmetically defined discontinuous groups" ''Ann. of Math.'' , '''72''' (1960) pp. 555–580 {{MR|0170356}} {{ZBL|0146.04701}} </TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> S. Zucker, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130040/s13004087.png" /> cohomology of warped products and arithmetic groups" ''Invent. Math.'' , '''70''' (1982) pp. 169–218 {{MR|0684171}} {{ZBL|0508.20020}} </TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> S. Zucker, "Satake compactifications" ''Comment. Math. Helv.'' , '''58''' (1983) pp. 312–343 {{MR|0705539}} {{ZBL|0565.22009}} </TD></TR></table> |
Revision as of 14:51, 24 March 2012
A type of compactification arising from work of I. Satake on the compactification of quotients of symmetric spaces by arithmetically-defined groups ([a9], [a10], [a11]). Below, the simplest case of this is presented first, to help suggest its generalization.
Let  be the upper half-plane, the symmetric space of non-compact type for
be the upper half-plane, the symmetric space of non-compact type for 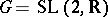 . For any subgroup
. For any subgroup  of finite index in
of finite index in  — these are arithmetic groups (cf. also Arithmetic group) — the quotient space
— these are arithmetic groups (cf. also Arithmetic group) — the quotient space  is a Riemann surface, a modular curve. A compactification
is a Riemann surface, a modular curve. A compactification  of
of  is obtained by first taking the
is obtained by first taking the  -invariant set
-invariant set
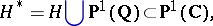 |
with an 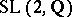 -equivariant topology that is the given one on
-equivariant topology that is the given one on 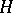 and makes
and makes 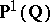 discrete; a deleted neighbourhood base for
discrete; a deleted neighbourhood base for 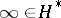 is given by
is given by
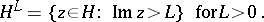 |
Then  is taken to be
is taken to be 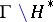 . It is a compact Riemann surface (thus automatically an algebraic curve). An important ingredient, both here and in Satake's generalization, is reduction theory. Relative to the point
. It is a compact Riemann surface (thus automatically an algebraic curve). An important ingredient, both here and in Satake's generalization, is reduction theory. Relative to the point 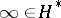 , it asserts that if
, it asserts that if 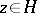 and
and 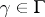 satisfy
satisfy 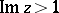 and
and 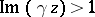 , then
, then 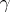 lies in the group of real translations (equivalently, in the parabolic group
lies in the group of real translations (equivalently, in the parabolic group 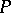 of upper-triangular matrices, which is the stabilizer of
of upper-triangular matrices, which is the stabilizer of 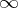 ). This gives an embedding of the punctured disc
). This gives an embedding of the punctured disc 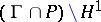 in
in 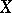 , and one is inserting the missing origin by adjoining
, and one is inserting the missing origin by adjoining 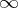 to
to 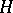 .
.
There was great interest in doing something similar for 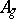 , the moduli space of Abelian varieties (cf. also Moduli theory; Abelian variety), which is the quotient
, the moduli space of Abelian varieties (cf. also Moduli theory; Abelian variety), which is the quotient 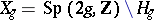 ; here,
; here, 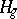 is the Siegel upper half-space of genus
is the Siegel upper half-space of genus 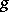 , which is the symmetric space for
, which is the symmetric space for  , the rank-
, the rank-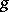 group of
group of 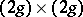 symplectic matrices. For
symplectic matrices. For 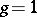 one has
one has 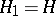 (from the preceding paragraph). Satake first observed, in [a9], that
(from the preceding paragraph). Satake first observed, in [a9], that 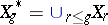 could be topologized in a way that makes it a compact space with "hereditary" structure: the closure of
could be topologized in a way that makes it a compact space with "hereditary" structure: the closure of 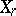 in
in 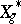 is homeomorphic to
is homeomorphic to 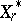 . Some refer to this space as "the" Satake compactification of
. Some refer to this space as "the" Satake compactification of 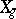 .
.
Satake compactifications, in the sense of [a13] (after [a11] and [a3]), are defined from the following setting [a10]. Let 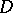 be the symmetric space of non-compact type for the real semi-simple Lie group
be the symmetric space of non-compact type for the real semi-simple Lie group  (cf. also Lie group, semi-simple). Each faithful finite-dimensional representation of
(cf. also Lie group, semi-simple). Each faithful finite-dimensional representation of 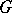 (cf. also Representation of a Lie algebra) determines an embedding of
(cf. also Representation of a Lie algebra) determines an embedding of 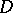 in some real projective space, so let
in some real projective space, so let 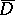 be the closure of
be the closure of  . The boundary of
. The boundary of 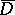 consists of pieces, called boundary components, that are homogeneous under a class of parabolic subgroups of
consists of pieces, called boundary components, that are homogeneous under a class of parabolic subgroups of 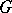 . If
. If  is the (real) rank of
is the (real) rank of 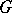 , there are only
, there are only 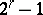 distinct such spaces
distinct such spaces 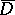 up to homeomorphism, corresponding to the non-empty subsets
up to homeomorphism, corresponding to the non-empty subsets 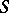 of a set of simple roots, and as such they form a semi-lattice; if one then writes
of a set of simple roots, and as such they form a semi-lattice; if one then writes  , the identity mapping of
, the identity mapping of 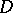 extends to a continuous mapping
extends to a continuous mapping 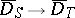 whenever
whenever 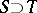 .
.
When 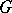 is the real Lie group associated to an algebraic group defined over
is the real Lie group associated to an algebraic group defined over 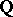 , a boundary component is said to be rational when its normalizing parabolic subgroup is defined over
, a boundary component is said to be rational when its normalizing parabolic subgroup is defined over 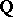 . Likewise, the structure over
. Likewise, the structure over  determines the class of arithmetic subgroups
determines the class of arithmetic subgroups 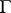 of
of 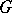 . Take
. Take 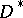 to be the union of
to be the union of 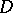 and its rational boundary components. Then, with a suitable topology on
and its rational boundary components. Then, with a suitable topology on 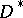 ,
, 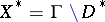 is, under mild hypotheses, a compactification of
is, under mild hypotheses, a compactification of 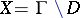 . The collection of these inherit the semi-lattice structure from the above. There is a precise sense in which the topology of
. The collection of these inherit the semi-lattice structure from the above. There is a precise sense in which the topology of  is induced from that of the closure of a Siegel set in
is induced from that of the closure of a Siegel set in 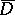 .
.
The Baily–Borel compactification is one of the minimal Satake compactifications in the case where 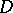 is Hermitian, i.e., has a
is Hermitian, i.e., has a  -invariant complex structure (cf. also Hermitian symmetric space). This includes the case of
-invariant complex structure (cf. also Hermitian symmetric space). This includes the case of  above. Here,
above. Here, 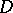 gets embedded as a bounded symmetric domain. By means of automorphic forms of sufficiently high weight,
gets embedded as a bounded symmetric domain. By means of automorphic forms of sufficiently high weight,  gets embedded as a normal algebraic subvariety of complex projective space [a2]. This fact has rather strong consequences, for the singular locus of
gets embedded as a normal algebraic subvariety of complex projective space [a2]. This fact has rather strong consequences, for the singular locus of 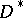 has "high" codimension in general, and one can invoke general results from algebraic geometry. It implies the existence of big families of Abelian varieties that do not degenerate. This compactification also enters into the topological interpretation of the
has "high" codimension in general, and one can invoke general results from algebraic geometry. It implies the existence of big families of Abelian varieties that do not degenerate. This compactification also enters into the topological interpretation of the 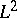 -cohomology of
-cohomology of 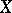 , as conjectured in [a12] and proved by E. Looijenga, and L. Saper and M. Stern.
, as conjectured in [a12] and proved by E. Looijenga, and L. Saper and M. Stern.
The applications of Satake compactifications cover a range of other areas. The stable cohomology of "the" Satake compactification was determined by R. Charney and R. Lee [a5] for application in 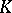 -theory. Non-Hermitian Satake compactifications occur in the combinatorial data of the toroidal compactifications of [a1] (see [a8], § 2), which provide resolution of the singularities of
-theory. Non-Hermitian Satake compactifications occur in the combinatorial data of the toroidal compactifications of [a1] (see [a8], § 2), which provide resolution of the singularities of  (cf. also Resolution of singularities).
(cf. also Resolution of singularities).
Another compactification, the reductive Borel–Serre, a simple quotient of the manifold-with-corners constructed in [a4] (see, e.g., [a7]), dominates all Satake compactifications, and often coincides with the unique maximal one. It has played an increasing role in the theory of automorphic forms. It is the natural place to study the 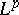 -cohomology [a12] and to define weighted cohomology [a6].
-cohomology [a12] and to define weighted cohomology [a6].
The spaces  (also defined in a different manner by H. Furstenberg) themselves have played an important role in harmonic analysis, rigidity theory and potential theory.
(also defined in a different manner by H. Furstenberg) themselves have played an important role in harmonic analysis, rigidity theory and potential theory.
References
| [a1] | A. Ash, D. Mumford, M. Rapoport, Y.-S. Tai, "Smooth compactification of locally symmetric varieties" , Math. Sci. Press (1975) MR0457437 Zbl 0334.14007 |
| [a2] | W. Baily, A. Borel, "Compactification of quotients of bounded symmetric domains" Ann. of Math. , 84 (1966) pp. 442–528 MR216035 Zbl 0154.08602 |
| [a3] | A. Borel, "Ensembles fondamentaux pour les groupes arithmétiques" Colloq. Théorie de Groupes Algébriques, Bruxelles (1962) pp. 23–40 MR0148666 Zbl 0161.02603 |
| [a4] | A. Borel, J.-P. Serre, "Corners and arithmetic groups" Comment. Math. Helv. , 48 (1973) pp. 436–491 MR0387495 Zbl 0274.22011 |
| [a5] | R. Charney, R. Lee, "Cohomology of the Satake compactification" Topology , 22 (1983) pp. 389–423 MR0715247 Zbl 0562.32017 |
| [a6] | M. Goresky, G. Harder, R. MacPherson, "Weighted cohomology" Invent. Math. , 116 (1994) pp. 139–213 MR1253192 Zbl 0849.11047 |
| [a7] | M. Goresky, Y.-S. Tai, "Toroidal and reductive Borel–Serre compactifications of locally symmetric spaces" Amer. J. Math. , 121 (1999) pp. 1095–1151 MR1712965 Zbl 1008.32014 |
| [a8] | M. Harris, S. Zucker, "Boundary cohomology of Shimura varieties, II: Hodge theory at the boundary" Invent. Math. , 116 (1994) pp. 243–307 MR1253194 Zbl 0860.11031 |
| [a9] | I. Satake, "On the compactification of the Siegel space" J. Indian Math. Soc. , 20 (1956) pp. 259–281 MR0084842 Zbl 0072.30002 |
| [a10] | I. Satake, "On representations and compactifications of symmetric Riemannian spaces." Ann. of Math. , 71 (1960) pp. 77–110 MR0118775 Zbl 0094.34603 |
| [a11] | I. Satake, "On compactifications of the quotient spaces for arithmetically defined discontinuous groups" Ann. of Math. , 72 (1960) pp. 555–580 MR0170356 Zbl 0146.04701 |
| [a12] | S. Zucker, " cohomology of warped products and arithmetic groups" Invent. Math. , 70 (1982) pp. 169–218 MR0684171 Zbl 0508.20020 cohomology of warped products and arithmetic groups" Invent. Math. , 70 (1982) pp. 169–218 MR0684171 Zbl 0508.20020 |
| [a13] | S. Zucker, "Satake compactifications" Comment. Math. Helv. , 58 (1983) pp. 312–343 MR0705539 Zbl 0565.22009 |
Satake compactification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Satake_compactification&oldid=16442