Generalized function
A mathematical concept generalizing the classical concept of a function. The need for such a generalization arises in many problems in engineering, physics and mathematics. The concept of a generalized function makes it possible to express in a mathematically-correct form such idealized concepts as the density of a material point, a point charge or a point dipole, the (space) density of a simple or double layer, the intensity of an instantaneous source, etc. On the other hand, the concept of a generalized function reflects the fact that in reality a physical quantity cannot be measured at a point; only its mean values over sufficiently small neighbourhoods of a given point can be measured. Thus, the technique of generalized functions serves as a convenient and adequate apparatus for describing the distributions of various physical quantities. Hence generalized functions are also called distributions.
Generalized functions were first introduced at the end of the 1920-s by P.A.M. Dirac (see [1]) in his research on quantum mechanics, in which he made systematic use of the concept of the 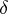 -function and its derivatives (see Delta-function). The foundations of the mathematical theory of generalized functions were laid by S.L. Sobolev [2] in 1936 by solving the Cauchy problem for hyperbolic equations, while in the 1950-s L. Schwartz (see [3]) gave a systematic account of the theory of generalized functions and indicated many applications. The theory was then intensively developed by many mathematicians and theoretical physicists, mainly in connection with the needs of theoretical and mathematical physics and the theory of differential equations (see [4]–[7]). The theory of generalized functions has made great advances, has numerous applications, and is extensively used in mathematics, physics and engineering.
-function and its derivatives (see Delta-function). The foundations of the mathematical theory of generalized functions were laid by S.L. Sobolev [2] in 1936 by solving the Cauchy problem for hyperbolic equations, while in the 1950-s L. Schwartz (see [3]) gave a systematic account of the theory of generalized functions and indicated many applications. The theory was then intensively developed by many mathematicians and theoretical physicists, mainly in connection with the needs of theoretical and mathematical physics and the theory of differential equations (see [4]–[7]). The theory of generalized functions has made great advances, has numerous applications, and is extensively used in mathematics, physics and engineering.
Formally, a generalized function 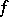 is defined as a continuous linear functional on some vector space of sufficiently "good" (test) functions
is defined as a continuous linear functional on some vector space of sufficiently "good" (test) functions  ;
; 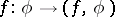 . An important example of a test space is the space
. An important example of a test space is the space  — the collection of
— the collection of 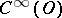 -functions on an open set
-functions on an open set 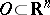 , with compact support in
, with compact support in 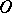 , endowed with the topology of the strong inductive limit (union) of the spaces
, endowed with the topology of the strong inductive limit (union) of the spaces 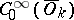 ,
, 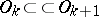 ,
, 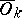 compact,
compact, 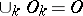 . The space
. The space 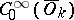 is the collection of
is the collection of 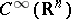 -functions with support in
-functions with support in  , with the topology given by the countable set of norms
, with the topology given by the countable set of norms
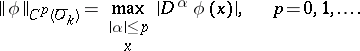 |
An example of a test function in 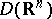 is the "cap functioncap" :
is the "cap functioncap" :
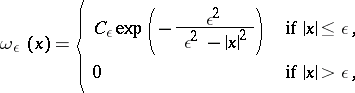 |
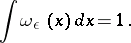 |
The space of generalized functions 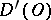 is the space dual to
is the space dual to 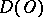 ;
; 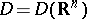 ,
, 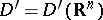 . Convergence of a sequence of generalized functions in
. Convergence of a sequence of generalized functions in 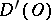 is defined as weak convergence of functionals in
is defined as weak convergence of functionals in 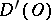 , that is,
, that is, 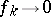 , as
, as 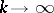 , in
, in  means that
means that 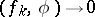 , as
, as 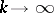 , for all
, for all 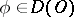 .
.
For a linear functional 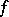 on
on 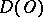 to be a generalized function in
to be a generalized function in 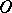 , that is,
, that is, 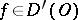 , it is necessary and sufficient that for any open set
, it is necessary and sufficient that for any open set 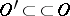 there exist numbers
there exist numbers 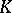 and
and 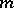 such that
such that
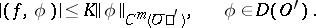 | (1) |
If the integer 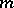 in (1) can be chosen independently of
in (1) can be chosen independently of 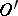 , then the generalized function
, then the generalized function 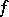 has finite order; the least such
has finite order; the least such 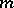 is called the order of
is called the order of 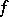 in
in 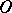 . Thus, by (1), every generalized function
. Thus, by (1), every generalized function  has finite order in any relatively compact
has finite order in any relatively compact 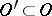 .
.
The space 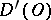 is complete: If a sequence of generalized functions
is complete: If a sequence of generalized functions 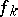 ,
,  in
in 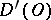 is such that for any
is such that for any 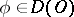 the sequence of numbers
the sequence of numbers 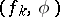 converges, then the functional
converges, then the functional
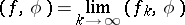 |
belongs to 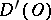 .
.
The simplest examples of generalized functions are those generated by locally integrable functions on 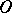 :
:
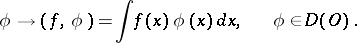 | (2) |
Generalized functions definable by (2) in terms of locally integrable functions 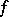 on
on 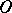 are called regular generalized functions on
are called regular generalized functions on 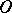 ; the remaining generalized functions are called singular. There is a one-to-one correspondence between locally integrable functions on
; the remaining generalized functions are called singular. There is a one-to-one correspondence between locally integrable functions on 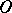 and regular generalized functions on
and regular generalized functions on  . In this sense, the "ordinary" , that is, locally integrable on
. In this sense, the "ordinary" , that is, locally integrable on 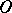 , functions are (regular) generalized functions in
, functions are (regular) generalized functions in 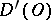 .
.
An example of a singular generalized function on  is the Dirac
is the Dirac 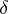 -function
-function
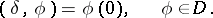 |
It describes the density of a unit mass concentrated at the point 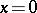 . The "cap"
. The "cap" 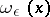 (weakly) approximates the
(weakly) approximates the 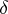 -function:
-function:
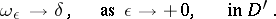 |
Let 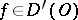 and let
and let 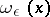 be a "cap" . Then the function
be a "cap" . Then the function
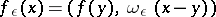 |
in 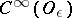 is called the regularization of
is called the regularization of 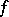 , and
, and 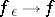 , as
, as 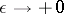 , in
, in 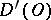 . Moreover, each
. Moreover, each  in
in  is the weak limit of functions in
is the weak limit of functions in 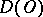 . The latter property is sometimes taken as the starting point for the definition of a generalized function; together with the theorem on the completeness of the space of generalized functions it leads to an equivalent definition of generalized functions [8].
. The latter property is sometimes taken as the starting point for the definition of a generalized function; together with the theorem on the completeness of the space of generalized functions it leads to an equivalent definition of generalized functions [8].
In general, a generalized function need not have a value at an individual point. Nonetheless, one speaks of a generalized function coinciding with a locally integrable function on an open set: A generalized function 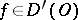 coincides on
coincides on 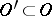 with a locally integrable function
with a locally integrable function 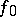 on
on 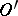 if its restriction to
if its restriction to 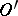 is
is 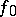 , that is, in accordance with (2), if
, that is, in accordance with (2), if
 |
for all 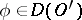 . One then says that
. One then says that 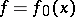 ,
, 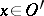 . In particular, with
. In particular, with 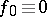 one obtains a definition of the vanishing of a generalized function
one obtains a definition of the vanishing of a generalized function 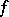 in
in 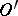 . The set of points
. The set of points  of
of 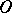 with the property that
with the property that 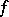 does not vanish on any neighbourhood of
does not vanish on any neighbourhood of  is called the support of
is called the support of 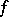 , denoted by
, denoted by 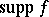 (cf. also Support of a generalized function). If
(cf. also Support of a generalized function). If 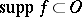 and is relatively compact, then
and is relatively compact, then  is called of compact support in
is called of compact support in 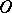 .
.
The following theorem on piecewise glueing generalized functions holds: Suppose that for each 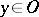 a generalized function
a generalized function 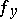 in
in 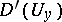 is given, where
is given, where 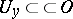 is a neighbourhood of
is a neighbourhood of 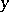 , so that the elements
, so that the elements 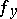 are compatible, that is,
are compatible, that is, 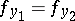 in
in 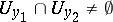 ; then there exists a generalized function
; then there exists a generalized function 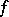 in
in  that coincides with
that coincides with 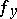 in
in 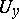 for all
for all 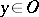 .
.
Examples of generalized functions.
1) The Dirac 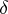 -function:
-function: 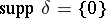 .
.
2) The generalized function 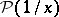 , defined by
, defined by
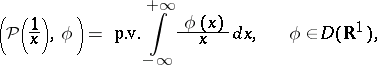 |
is called the finite part, or principal value, of the integral of 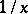 ;
;  . The distribution
. The distribution 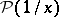 is singular on
is singular on 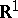 , but on the open set
, but on the open set 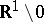 it is regular and coincides with
it is regular and coincides with 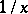 .
.
3) The surface 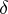 -function. Let
-function. Let 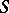 be a piecewise-smooth surface and let
be a piecewise-smooth surface and let 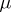 be a continuous function on
be a continuous function on 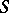 . The generalized function
. The generalized function 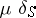 is defined by
is defined by
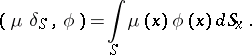 |
Here 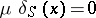 for
for 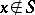 , and
, and 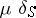 is a singular function. This generalized function describes the space density of masses or charges concentrated on
is a singular function. This generalized function describes the space density of masses or charges concentrated on 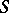 with surface density
with surface density 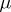 (density of a simple layer).
(density of a simple layer).
Linear operations on generalized functions are introduced as extensions of the corresponding operations on the test functions.
Change of variables.
Let 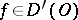 and let
and let 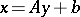 be a linear transformation of
be a linear transformation of 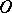 onto
onto 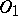 . The generalized function
. The generalized function  in
in 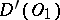 is defined by
is defined by
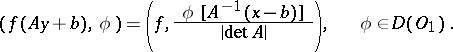 | (3) |
Since the operation 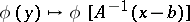 is an isomorphism of
is an isomorphism of  onto
onto 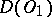 , the operation
, the operation 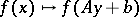 is an isomorphism of
is an isomorphism of 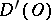 onto
onto 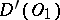 . In particular, if
. In particular, if 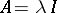 ,
, 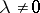 ,
, 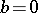 (
(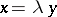 is a similarity (with a reflection if
is a similarity (with a reflection if 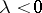 )), then
)), then
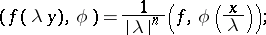 |
if 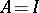 (
( is a shift by
is a shift by 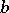 ), then
), then
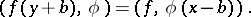 |
Formula (3) enables one to define generalized functions that are translation invariant, spherically symmetric, centrally symmetric, homogeneous, periodic, Lorentz invariant, etc.
Let the function 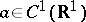 have only simple zeros
have only simple zeros 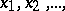 on the line
on the line 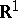 . The function
. The function 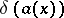 is defined by
is defined by
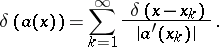 |
Examples.
4) 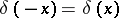 .
.
5) 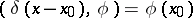 .
.
6) 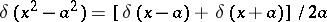 ,
, 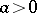 .
.
7) 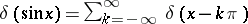 .
.
Products.
Let 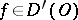 and
and 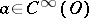 . The product
. The product 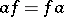 is defined by
is defined by
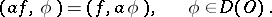 |
It turns out that 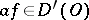 , and for ordinary integrable functions
, and for ordinary integrable functions 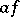 coincides with the usual multiplication of the functions
coincides with the usual multiplication of the functions 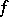 and
and  (cf. also Generalized functions, product of).
(cf. also Generalized functions, product of).
Examples.
8) 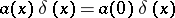 .
.
9) 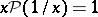 .
.
However, this product operation cannot be extended to arbitrary generalized functions in such a way that it is associative and commutative. In fact, if this could be done, then one obtains a contradiction:
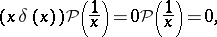 |
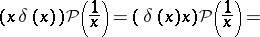 |
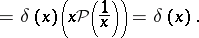 |
Such a product can be defined for certain classes of generalized functions, but it may fail to be uniquely defined.
Differentiation.
Let 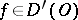 . The generalized (weak) derivative of
. The generalized (weak) derivative of 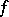 ,
,
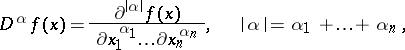 |
of order 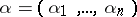 is defined by
is defined by
 | (4) |
Since the operation 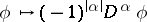 is linear and continuous from
is linear and continuous from 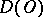 into
into 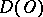 , the functional
, the functional 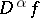 defined by the right-hand side of (4) is a generalized function in
defined by the right-hand side of (4) is a generalized function in 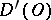 . If
. If  , then
, then 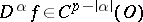 for all
for all 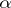 with
with 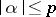 .
.
The following properties hold: the operation 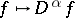 is linear and continuous from
is linear and continuous from 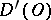 into
into 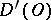 , and any generalized function in
, and any generalized function in 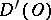 is infinitely differentiable (in the generalized sense); the derivative does not depend on the order of differentiation; the Leibniz formula is valid for the differentiation of a product
is infinitely differentiable (in the generalized sense); the derivative does not depend on the order of differentiation; the Leibniz formula is valid for the differentiation of a product 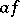 , where
, where 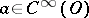 ; differentiation does not enlarge the support; for any open set
; differentiation does not enlarge the support; for any open set 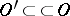 , every generalized function in
, every generalized function in 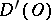 is a derivative of a continuous function in
is a derivative of a continuous function in 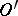 ; any differential equation
; any differential equation 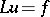 ,
,  , with constant coefficients can be solved in
, with constant coefficients can be solved in 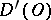 , if
, if 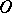 is a convex domain; any generalized function of order
is a convex domain; any generalized function of order 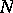 with support at the point
with support at the point  can be uniquely represented in the form
can be uniquely represented in the form
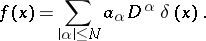 |
Examples.
10) 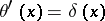 , where
, where 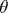 is the Heaviside function (jump function):
is the Heaviside function (jump function):
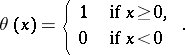 |
11) 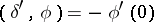 ;
; 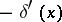 describes the charge density of a dipole of moment
describes the charge density of a dipole of moment 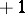 at the point
at the point 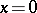 , oriented along the positive
, oriented along the positive  -axis.
-axis.
12) The normal derivative of the density of a simple layer on an orientable surface 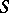 is a generalization of
is a generalization of 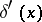 :
:
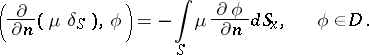 |
The generalized function 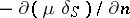 describes the space charge density corresponding to a distribution of dipoles on
describes the space charge density corresponding to a distribution of dipoles on 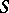 with moment surface density
with moment surface density 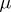 and oriented along a given direction of the normal
and oriented along a given direction of the normal  to
to 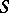 (density of a double layer).
(density of a double layer).
13) The general solution of the equation  in the class
in the class 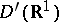 is
is 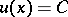 , where
, where 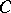 is an arbitrary constant.
is an arbitrary constant.
14) The general solution of the equation 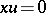 in the class
in the class 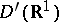 is
is 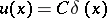 .
.
15) 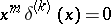 ,
, 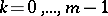 .
.
16) The trigonometric series
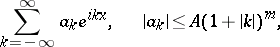 |
converges in 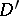 ; it can be differentiated term by term infinitely many times in
; it can be differentiated term by term infinitely many times in 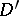 .
.
17) 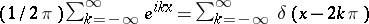 .
.
Cf. also Generalized function, derivative of a.
Direct products.
Let 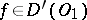 and
and 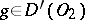 . Their direct product is defined by the formula
. Their direct product is defined by the formula
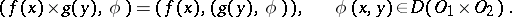 | (5) |
Since the operation 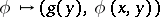 is linear and continuous from
is linear and continuous from 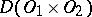 into
into 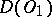 , the functional
, the functional 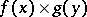 , defined by (5), is a generalized function in
, defined by (5), is a generalized function in  . The direct product is a commutative and associative operation, and
. The direct product is a commutative and associative operation, and
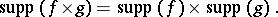 |
A generalized function 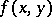 in
in 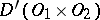 does not depend on
does not depend on 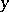 if it can be represented in the form
if it can be represented in the form
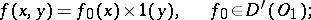 |
in this case one writes 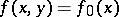 .
.
Examples.
18) 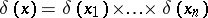 .
.
19) The general solution in 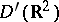 of the equation for the vibration of a homogeneous string,
of the equation for the vibration of a homogeneous string, 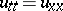 , is given by
, is given by
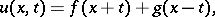 |
where 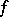 and
and 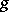 are arbitrary generalized functions in
are arbitrary generalized functions in 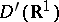 .
.
Convolution.
Let 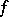 and
and 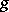 be generalized functions in
be generalized functions in 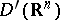 with the property that their direct product
with the property that their direct product 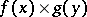 can be extended to functions of the form
can be extended to functions of the form 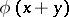 , where
, where 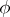 runs through
runs through 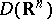 , in the following sense: For every sequence of functions
, in the following sense: For every sequence of functions 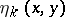 in
in 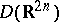 with the properties
with the properties
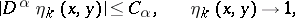 |
 |
(on any compact set), the sequence of numbers 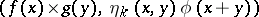 has a limit independent of the sequence
has a limit independent of the sequence 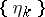 . This limit is called the convolution of
. This limit is called the convolution of 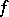 and
and 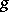 , and is denoted by
, and is denoted by  . Thus,
. Thus,
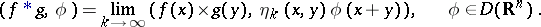 | (6) |
The completeness of 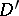 implies that
implies that 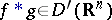 . As elementary examples show, the convolution does not exist for all pairs
. As elementary examples show, the convolution does not exist for all pairs 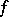 and
and 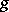 . It does exists if one of the generalized functions is of compact support. If the convolution exists in
. It does exists if one of the generalized functions is of compact support. If the convolution exists in 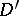 , then it is commutative,
, then it is commutative, 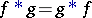 , and the following formulas for the differentiation of a convolution are valid:
, and the following formulas for the differentiation of a convolution are valid:
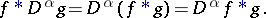 | (7) |
Also
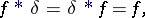 | (8) |
hence, from (7),
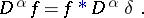 |
Finally
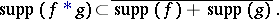 |
The example
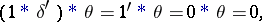 |
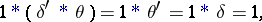 |
shows that convolution is a non-associative operation. However, associative (and commutative) convolution algebras exist. By (8), the 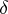 -function is the identity element in them. For example, a convolution algebra is formed by the set
-function is the identity element in them. For example, a convolution algebra is formed by the set 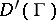 consisting of the generalized functions in
consisting of the generalized functions in 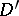 with support in a convex acute closed cone
with support in a convex acute closed cone 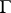 with vertex at
with vertex at  . One writes:
. One writes:
 |
A generalized function  in
in 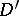 is called a fundamental solution (point-source function) of a differential operator
is called a fundamental solution (point-source function) of a differential operator 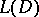 with constant coefficients if it satisfies the equation
with constant coefficients if it satisfies the equation
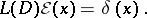 |
If a fundamental solution 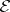 of
of 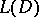 is known, then a solution can be constructed for the equation
is known, then a solution can be constructed for the equation 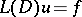 for those
for those  in
in 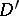 for which the convolution
for which the convolution  exists, and this solution is given by
exists, and this solution is given by 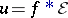 .
.
Examples.
20) The kernel of a fractional differentiation or integration operator 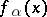 ,
, 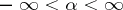 :
:
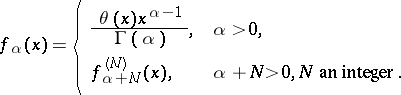 |
Here 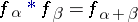 ,
, 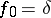 ,
, 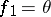 ,
, 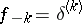 ,
, 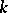 an integer. If
an integer. If 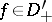 , then
, then  is the primitive of order
is the primitive of order 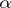 for
for 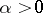 (derivative of order
(derivative of order 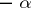 for
for 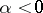 ).
).
21) 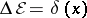 ,
,
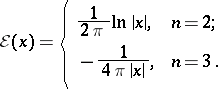 |
22) 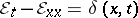 ,
,
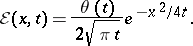 |
23) 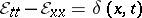 ,
,
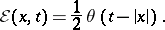 |
Fourier transformation.
It is defined on the class 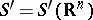 of generalized functions of slow growth. The space of test functions
of generalized functions of slow growth. The space of test functions 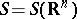 consists of the
consists of the 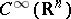 -functions that decrease at infinity together with all their derivatives faster than any power of
-functions that decrease at infinity together with all their derivatives faster than any power of 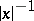 . The topology of
. The topology of 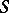 is given by the countable set of norms
is given by the countable set of norms
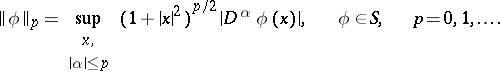 |
Here 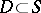 and
and 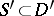 , and these imbeddings are continuous. Functions of slow growth that are locally integrable on
, and these imbeddings are continuous. Functions of slow growth that are locally integrable on 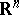 are in
are in 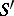 , and define regular functionals on
, and define regular functionals on 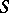 by formula (2).
by formula (2).
Every generalized function in 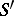 is a derivative of a continuous function of slow growth, and so has finite order on
is a derivative of a continuous function of slow growth, and so has finite order on 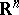 .
.
The Fourier transform 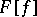 of a generalized function
of a generalized function 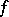 in
in 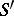 is defined by the equation
is defined by the equation
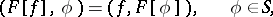 |
where
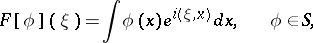 |
is the classical Fourier transform. Since the operation 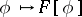 is an isomorphism of
is an isomorphism of 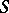 onto
onto 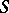 , the operation
, the operation 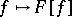 is an isomorphism of
is an isomorphism of 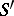 onto
onto 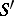 , and the inverse of
, and the inverse of  is given by
is given by
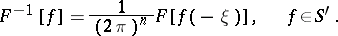 |
The following basic formulas hold for 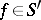 :
:
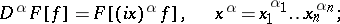 |
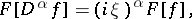 |
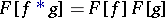 |
if  has compact support. If the generalized function
has compact support. If the generalized function 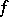 is periodic with
is periodic with  -period
-period 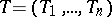 ,
, 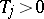 , then
, then 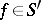 , and it can be expanded in a trigonometric series
, and it can be expanded in a trigonometric series
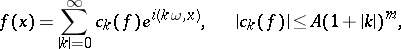 |
converging to 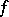 in
in 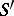 . Here
. Here
 |
Examples.
24) 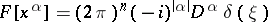 ; in particular,
; in particular, 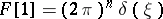 .
.
25) 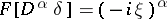 ; in particular,
; in particular, 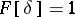 .
.
26) 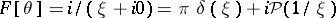 .
.
Cf. also Fourier transform of a generalized function.
Laplace transformation.
Let the generalized function 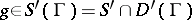 , where
, where 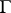 is a closed convex acute cone. Let
is a closed convex acute cone. Let 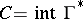 , where
, where 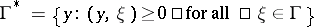 is the cone dual to
is the cone dual to 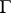 . The Laplace transform of
. The Laplace transform of 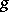 is defined by
is defined by
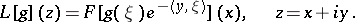 | (9) |
The mapping 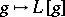 defines an isomorphism of the convolution algebra
defines an isomorphism of the convolution algebra 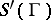 onto the algebra
onto the algebra 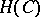 consisting of the functions
consisting of the functions  that are holomorphic in the wedge
that are holomorphic in the wedge 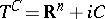 and that satisfy the following growth condition: There exist numbers
and that satisfy the following growth condition: There exist numbers 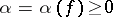 and
and 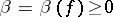 such that for any cone
such that for any cone 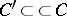 (i.e.
(i.e. 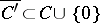 ) there exists a number
) there exists a number 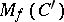 such that
such that
 |
The inverse of the Laplace transform 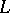 is given by the equation
is given by the equation
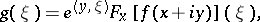 | (10) |
where the right-hand side of (10) is independent of 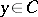 .
.
The one-to-one correspondence between 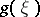 and
and 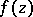 given by equations (9) and (10) can be conveniently represented by the following scheme:
given by equations (9) and (10) can be conveniently represented by the following scheme:
 |
in which 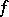 is called the transform of
is called the transform of 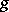 , and
, and 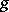 the spectral function of
the spectral function of  .
.
Every 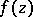 in the algebra
in the algebra 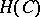 has a boundary value
has a boundary value 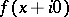 as
as 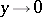 ,
, 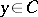 , in
, in 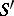 , related to the spectral function
, related to the spectral function  of
of 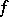 by the formula
by the formula 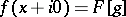 according to (9). The following basic formulas hold for the Laplace transform:
according to (9). The following basic formulas hold for the Laplace transform:
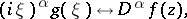 |
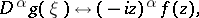 |
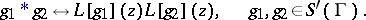 |
Example.
27) 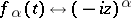 ; in particular,
; in particular,
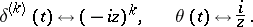 |
References
| [1] | P.A.M. Dirac, "The principles of quantum mechanics" , Clarendon Press (1947) MR0023198 Zbl 0030.04801 |
| [2] | S.L. Sobolev, "Méthode nouvelle à résoudre le problème de Cauchy pour les équations linéaires hyperboliques normales" Mat. Sb. , 1 (1936) pp. 39–72 |
| [3] | L. Schwartz, "Théorie des distributions" , 1–2 , Hermann (1950–1951) MR2067351 MR0209834 MR0117544 MR0107812 MR0041345 MR0035918 MR0032815 MR0031106 MR0025615 Zbl 0962.46025 Zbl 0653.46037 Zbl 0399.46028 Zbl 0149.09501 Zbl 0085.09703 Zbl 0089.09801 Zbl 0089.09601 Zbl 0078.11003 Zbl 0042.11405 Zbl 0037.07301 Zbl 0039.33201 Zbl 0030.12601 |
| [4] | N.N. Bogolyubov, A.A. Logunov, I.T. Todorov, "Introduction to axiomatic quantum field theory" , Benjamin (1975) (Translated from Russian) MR452277 |
| [5] | I.M. Gel'fand, G.E. Shilov, "Generalized functions" , 1–5 , Acad. Press (1966–1968) (Translated from Russian) Zbl 0801.33020 Zbl 0699.33012 Zbl 0159.18301 Zbl 0355.46017 Zbl 0144.17202 Zbl 0115.33101 Zbl 0108.29601 |
| [6] | V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian) MR0764399 Zbl 0954.35001 Zbl 0652.35002 Zbl 0695.35001 Zbl 0699.35005 Zbl 0607.35001 Zbl 0506.35001 Zbl 0223.35002 Zbl 0231.35002 Zbl 0207.09101 |
| [7] | V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1979) (Translated from Russian) MR0564116 MR0549767 Zbl 0515.46034 Zbl 0515.46033 |
| [8] | P. Antosik, J. Mikusiński, R. Sikorski, "Theory of distributions. The sequential approach" , Elsevier (1973) MR0365130 Zbl 0267.46028 |
Comments
The notation 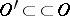 means that the closure
means that the closure 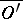 is contained in
is contained in 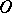 . Usually the support of a function (or distribution) is defined as the closure of the set of points where it is non-zero.
. Usually the support of a function (or distribution) is defined as the closure of the set of points where it is non-zero.
References
| [a1] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5 MR0617913 Zbl 0435.46002 |
| [a2] | D.S. Jones, "The theory of generalized functions" , Cambridge Univ. Press (1982) |
| [a3] | W. Rudin, "Functional analysis" , McGraw-Hill (1974) MR1157815 MR0458106 MR0365062 Zbl 0867.46001 Zbl 0253.46001 |
| [a4] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1 , Springer (1983) MR0717035 MR0705278 Zbl 0521.35002 Zbl 0521.35001 |
Generalized function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Generalized_function&oldid=34447