Zolotarev polynomials
Zolotareff polynomials, Solotareff polynomials
For each $\sigma \in \mathbf{R}$, the Zolotarev polynomial $Z _ { n } ( x ; \sigma )$ is the unique solution of the problem
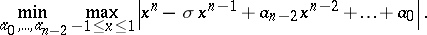 |
That is, the Zolotarev polynomials of degree $n$ are the polynomials whose leading two coefficients are fixed, and that deviate least from zero on the interval $[ - 1,1 ]$, in the uniform norm (cf. also Uniform approximation; Polynomial least deviating from zero).
This problem was formulated and solved by E.I. Zolotarev. It is the first of four Zolotarev problems in approximation theory. Zolotarev's second problem asks for the monic polynomial $p$ of degree $n$ that deviates least from zero on the interval $[ - 1,1 ]$ while satisfying the extra condition $p ( \xi ) = \eta$ for some $\xi > 1$ and $\eta \in \mathbf{R}$. The class of solutions (dependent on $\xi $ and $ \eta $) are normalized Zolotarev polynomials. The third and fourth problems of Zolotarev deal with rational functions.
In each of these problems the influence of P.L. Chebyshev can be seen, whose lectures Zolotarev attended, as these problems are all generalizations of problems of Chebyshev. $T _ { n }$, the monic Chebyshev polynomial of degree $n$, solves problem one but without any restriction on the coefficient of $x ^ { n - 1 }$, cf. Chebyshev polynomials. (From symmetry considerations, $T _ { n } ( . ) = Z _ { n } (\, . \, ; 0 )$.)
It follows from the equi-oscillation theorem in the theory of best uniform approximation that $Z _ { n } ( x ; \sigma )$ is uniquely determined by the fact that the coefficients of $x ^ { n }$ and $x ^ { n - 1 }$ are as given, and it attains its norm, alternately in sign, at least $n$ times in $[ - 1,1 ]$. Thus it is easily verified that for $0 \leq \sigma \leq ( 1 / n ) \operatorname { tan } ^ { 2 } ( \pi / 2 n )$,
\begin{equation*} Z _ { n } ( x ; \sigma ) = ( 1 + \sigma ) ^ { n } T _ { n } \left( \frac { x - \sigma } { 1 + \sigma } \right) \end{equation*}
(which is what one gets when the Chebyshev polynomial is fixed at $- 1$ and pulled to the right as long as the resulting polynomial attains its norm alternately at $n$ points in $[ - 1,1 ]$). For $\sigma > ( 1 / n ) \operatorname { tan } ^ { 2 } ( \pi / 2 n )$ the Zolotarev polynomial is given in terms of elliptic integrals, see e.g. [a1], [a4], [a6], [a3] for more details. It suffices to consider $\sigma \geq 0$, since $Z _ { n } ( x ; - \sigma ) = ( - 1 ) ^ { n } Z _ { n } ( - x ; \sigma )$.
Zolotarev polynomials, suitably normalized, are also the class of extremal polynomials in the pointwise Markov inequalities, cf. Markov inequality. That is, they maximize
\begin{equation*} | p ^ { ( k ) } ( \xi ) | \end{equation*}
for fixed $\xi \in ( - 1,1 )$ and $1 \leq k \leq n - 1$, over all polynomials of degree at most $n$ which are bounded by $1$ on $[ - 1,1 ]$. (For $| \xi | \geq 1$ the extremal polynomial is always the Chebyshev polynomial.) This problem is considered in detail in [a9] (see especially the index).
Various generalizations of Zolotarev polynomials can be found in the literature. The problem of finding the extremal polynomials when $r$ coefficients, rather than just $2$ coefficients, are fixed was considered by A. Akhiezer and by N.N. Meiman. For a generalization of the first Zolotarev problem to different (symmetric) domains and $\sigma \in \mathbf{C}$, see [a7] and references therein. Zolotarev perfect splines and Zolotarev $\omega$-polynomials were introduced when generalizing the pointwise Markov inequalities to other spaces of functions, see e.g. [a5], [a8], and [a2].
Due to fashions in transliteration, Zolotarev's name is sometimes written as Zolotareff or Solotareff.
References
| [a1] | A. Achieser, "Theory of approximation" , F. Ungar (1956) (In Russian) |
| [a2] | S.K. Bagdasarov, "Zolotarev $\omega$-polynomials in $W ^ { r} H ^ { \omega } [ 0,1 ]$" J. Approx. Th. , 90 (1997) pp. 340–378 |
| [a3] | B.C. Carlson, J. Todd, "Zolotarev's first problem: the best approximation by polynomials of degree $\leq n - 2$ to $x ^ { n } - n \sigma x ^ { n - 1 }$ in $[ - 1,1 ]$" Aequat. Math. , 26 (1983) pp. 1–33 |
| [a4] | P. Erdős, G. Szegő, "On a problem of I. Schur" Ann. Math. , 43 (1942) pp. 451–470 (Correction: 74 (1961), 628; Reprinted in G. Szegő, Collected Papers (R.A. Askey, ed.), Vol. 2 (1982), 807-827, Birkhäuser) |
| [a5] | S. Karlin, "Oscillatory perfect splines and related extremal problems" S. Karlin (ed.) C.A. Micchelli (ed.) A. Pinkus (ed.) I.J. Schoenberg (ed.) , Spline Functions and Approximation Theory , Acad. Press (1976) pp. 371–460 |
| [a6] | S. Paszkowski, "The theory of uniform approximation I. Non-asymptotic theoretical problems" Rozp. Mat. , 26 (1962) |
| [a7] | F. Peherstorfer, K. Schiefermayr, "Explicit generalized Zolotarev polynomials with complex coefficients II" East J. Approx. , 3 (1997) pp. 473–483 |
| [a8] | A. Pinkus, "Some extremal properties of perfect splines and the pointwise Landau problem on the finite interval" J. Approx. Th. , 23 (1978) pp. 37–64 |
| [a9] | E.V. Voronovskaja, "The functional method and its applications" Transl. Math. Monographs , 28 (1970) |
Zolotarev polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zolotarev_polynomials&oldid=54330