User:Ulf Rehmann/Test5
From Encyclopedia of Mathematics
Algebraic curve
| Nr. | Image of png File | $\TeX$, 1st version | $\TeX$, 2nd version | Confidence, F?
name of png |
|---|---|---|---|---|
| Algebraic curve | ||||
| 1.(23.) | 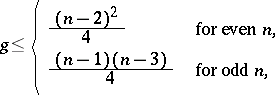 |
$g \leq \left\{ \begin{array} { l l } { \frac { ( n - 2 ) ^ { 2 } } { 4 } } & { \text { for even } n } \\ { \frac { ( n - 1 ) ( n - 3 ) } { 4 } } & { \text { for odd } n } \end{array} \right.$ | $$ g \leq \left\{ \begin{array} { l l } { \frac { ( n - 2 ) ^ { 2 } } { 4 } } & { \text { for even } n, } \\ { \frac { ( n - 1 ) ( n - 3 ) } { 4 } } & { \text { for odd } n, } \end{array} \right.$$ | conf 0.698
png = a01145065.png (65) |
Algebraic geometry
| Nr. | Image of png File | $\TeX$, 1st version | $\TeX$, 2nd version | Confidence, F?
name of png |
|---|---|---|---|---|
| Algebraic geometry | ||||
| 2.(116.) | 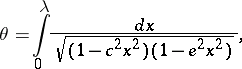 |
$\theta = \int _ { 0 } ^ { \lambda } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } }$ | $$\empty$$ | conf 0.997
png = a01150014.png(14) |
| 3.(133.) |  |
$\omega = 2 \int _ { 0 } ^ { 1 / c } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } }$ | $$\empty$$ | conf 0.973
png = a01150021.png(21) |
| 4.(67.) |  |
$\overline { w } = 2 \int _ { 0 } ^ { 1 / \varepsilon } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } }$ | $$\widetilde{ w } = 2 \int _ { 0 } ^ { 1 / \varepsilon } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } },$$ | conf 0.107
png = a01150022.png(22) |
| 5.(105.) |  |
$\theta ( v + \pi i r ) = \theta ( r ) , \quad \theta ( v + \alpha _ { j } ) = e ^ { L _ { j } ( v ) } \theta ( v )$ | $$\empty$$ | conf 0.775
png = a01150044.png(44) |
| 6.(17.) |  |
$\left( \begin{array} { l l } { \alpha } & { b } \\ { c } & { d } \end{array} \right) \equiv \left( \begin{array} { l l } { 1 } & { 0 } \\ { 0 } & { 1 } \end{array} \right) ( \operatorname { mod } 7 )$ | $$\empty$$ | conf 0.440
png = a01150078.png(78) |
Algebraic surface
!colspan="5" | Algebraic surface
| Nr. | Image of png File | $\TeX$, 1st version | $\TeX$, 2nd version | Confidence, F?
name of png |
|---|---|---|---|---|
| 7.(144.) | 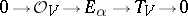 |
$0 \rightarrow O _ { V } \rightarrow E _ { \alpha } \rightarrow T _ { V } \rightarrow 0$ | $$0 \rightarrow {\cal O} _ { V } \rightarrow E _ { \alpha } \rightarrow T _ { V } \rightarrow 0$$ | conf 0.981
png = a011640132.png(132) |
| 8.(73.) | 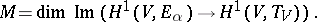 |
$M = \operatorname { dim } \operatorname { Im } ( H ^ { 1 } ( V , E _ { \alpha } ) \rightarrow H ^ { 1 } ( V , T _ { V } ) )$ | $$\empty$$ | conf 0.997
png = a011640137.png(137) |
| 9.(88.) | 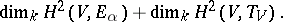 |
$\operatorname { dim } _ { k } H ^ { 2 } ( V , E _ { \alpha } ) + \operatorname { dim } _ { k } H ^ { 2 } ( V , T _ { V } )$ | $$\empty$$ | conf 0.996
png = a011640139.png(139) |
| 10.(117.) | 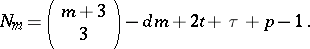 |
$N _ { m } = \left( \begin{array} { c } { m + 3 } \\ { 3 } \end{array} \right) - d m + 2 t + \tau + p - 1$ | $$\empty$$ | conf 0.369
png = a01164027.png(27) |
| 11.(72.) | 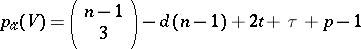 |
$p _ { \alpha } ( V ) = \left( \begin{array} { c } { n - 1 } \\ { 3 } \end{array} \right) - d ( n - 1 ) + 2 t + \tau + p - 1$ | $$\empty$$ | conf 0.396
png = a01164029.png(29) |
| 12.(68.)* | 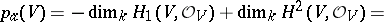 |
$p _ { x } ( V ) = - \operatorname { dim } _ { k } H _ { 1 } ( V , O _ { V } ) + \operatorname { dim } _ { k } H ^ { 2 } ( V , O _ { V } ) =$ | $$p _ { \alpha } ( V ) = - \operatorname { dim } _ { k } H _ { 1 } ( V , {\cal O} _ { V } ) + \operatorname { dim } _ { k } H ^ { 2 } ( V , {\cal O} _ { V } ) =$$ | conf 0.756 F
png = a01164047.png(47) |
| 13.(93.)* | 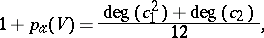 |
$1 + p _ { x } ( V ) = \frac { \operatorname { deg } ( c _ { 1 } ^ { 2 } ) + \operatorname { deg } ( c _ { 2 } ) } { 12 }$ | $$ 1 + p _ { \alpha } ( V ) = \frac { \operatorname { deg } ( c _ { 1 } ^ { 2 } ) + \operatorname { deg } ( c _ { 2 } ) } { 12 },$$ | conf 0.752 F
png = a01164053.png(53) |
Cartan subalgebra
| Nr. | Image of png File | $\TeX$, 1st version | $\TeX$, 2nd version | Confidence, F?
name of png |
|---|---|---|---|---|
| 14.(33.)* | 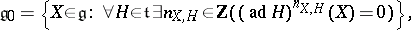 |
$\mathfrak { g } 0 = \{ X \in \mathfrak { g } : \forall H \in \mathfrak { t } \exists \mathfrak { n } X , H \in Z ( ( \text { ad } H ) ^ { n } X , H ( X ) = 0 ) \}$ | $$\mathfrak { g }_0 = \big\{ X \in \mathfrak { g } : \forall H \in \mathfrak { t } \exists { n }_{X,H} \in {\mathbb Z} ( ( \text { ad } H ) ^ { n_{X , H} } ( X ) = 0 ) \big\}$$ | conf 0.110 F
png = c0205509.png(9) |
How to Cite This Entry:
Ulf Rehmann/Test5. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ulf_Rehmann/Test5&oldid=44165
Ulf Rehmann/Test5. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ulf_Rehmann/Test5&oldid=44165