User:Maximilian Janisch/latexlist/Algebraic Groups/Quantum groups
The phrase "quantum group" is more or less a synonym for "Hopf algebra" . More precisely, the category of quantum groups is defined in [a1] to be dual to the category of Hopf algebras. This is natural for the following reason. There is the following general principle: The functor $i$ is an anti-equivalence between the category of "spaces" and the category of commutative associative unital algebras, perhaps with some additional structures or properties (this principle becomes a theorem if "space" is understood to be "affine scheme" or "compact topological space" , and "algebra" is understood to mean "C*-algebra" ). So one can translate the definition of a group into the language of algebras: instead of a space $k$ with an associative operation $G \times G \rightarrow G$ one obtains a commutative algebra $4$ over a commutative ring $k$ with a homomorphism $\Delta : A \rightarrow A \otimes A$, called comultiplication; the unit $\varepsilon \in C$ gives rise to a homomorphism $\epsilon : A \rightarrow k$, called co-unit, and the mapping $g \mapsto g ^ { - 1 }$, $g \in G$, gives rise to a bijective $k$-linear mapping $S : A \rightarrow A \otimes A$, called antipode. The group axioms are equivalent to the commutativity of the following diagrams:
 |
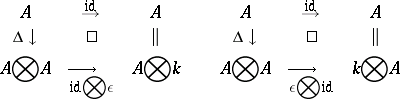 |
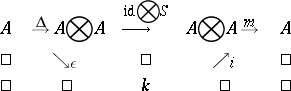 |
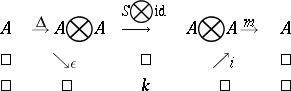 |
Here $m ( \alpha \otimes b ) = \alpha b$, $i ( c ) = c .1 _ { A }$. The commutativity of these diagrams means that $( A , \Delta , \epsilon , S )$ is a commutative Hopf algebra. Since the category of groups is anti-equivalent to the category of commutative Hopf algebras, it is natural to define a quantum group as an object of the category dual to the category of (not necessarily commutative) Hopf algebras.
A simple class of non-commutative Hopf algebras is formed by the group algebras of non-commutative groups. These Hopf algebras are commutative, i.e. $\Delta ( A )$ is contained in the symmetric part of $A \otimes A$. Essentially, all cocommutative Hopf algebras are group algebras.
Here is an example of a Hopf algebra which is neither commutative nor cocommutative. Fix $n \in N$ and $q \in k$, where $k$ is a commutative ring. Denote by $4$ the associative $k$-algebra with generators $x _ { i }$, $1 \leq i , j \leq n$, and defining relations 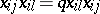 if $j < l$, $x _ { j } ; x _ { k } j = q x _ { k } ; x _ { j }$ if $i < k$, $x _ { i l } | x _ { k j } = x _ { k } ; x _ { i l }$ if $i < k$, $i > j$, $[ x _ { i l } , x _ { k j } ] = ( q ^ { - 1 } - q ) x _ { j } x _ { k l }$ if $i > k$, $i > j$,
if $j < l$, $x _ { j } ; x _ { k } j = q x _ { k } ; x _ { j }$ if $i < k$, $x _ { i l } | x _ { k j } = x _ { k } ; x _ { i l }$ if $i < k$, $i > j$, $[ x _ { i l } , x _ { k j } ] = ( q ^ { - 1 } - q ) x _ { j } x _ { k l }$ if $i > k$, $i > j$,  , where $l ( i _ { 1 } , \dots , i _ { n } )$ is the number of inversions in the permutation $( i _ { 1 } , \ldots , i _ { n } )$. Then $4$ has a Hopf algebra structure defined by $\Delta ( x _ { j } ) = \sum _ { k } x _ { i k } \otimes x _ { k j }$. If $q = 1$, then $4$ is the algebra of polynomial functions on $SL ( n )$. So, in the general case it is natural to consider elements of $4$ as "functions on the quantized SLn" .
, where $l ( i _ { 1 } , \dots , i _ { n } )$ is the number of inversions in the permutation $( i _ { 1 } , \ldots , i _ { n } )$. Then $4$ has a Hopf algebra structure defined by $\Delta ( x _ { j } ) = \sum _ { k } x _ { i k } \otimes x _ { k j }$. If $q = 1$, then $4$ is the algebra of polynomial functions on $SL ( n )$. So, in the general case it is natural to consider elements of $4$ as "functions on the quantized SLn" .
The quantized $SL ( n )$ is one of the simplest quantum groups which appear naturally in the theory of quantum integrable systems and, especially, in the quantum inverse-scattering method [a2]. The development of this method has led to the following quantization technique for constructing non-commutative non-cocommutative Hopf algebras. It is natural to construct them as deformations of commutative Hopf algebras. If a non-commutative deformation $4$ of a commutative Hopf algebra $A _ { 0 }$ is given, then a Poisson bracket on $A _ { 0 }$ is defined by $\{ a , b \} = \operatorname { lim } _ { h \rightarrow 0 } h ^ { - 1 } ( a b - b a )$, where $h$ is the deformation parameter and $a b$ means the deformed product, which is not commutative. This Poisson bracket has the usual properties (skew-symmetry, Jacobi identity, $\{ \alpha , b c \} = \{ \alpha , b \} c + \{ \alpha , c \} b$) and is compatible with comultiplication. In other words, $A _ { 0 }$ is a Poisson–Hopf algebra. Therefore it is natural to start with a Poisson–Hopf algebra $A _ { 0 }$ and then try to quantize it, i.e. to construct a Hopf algebra deformation of $A _ { 0 }$ which induces the given Poisson bracket on $A _ { 0 }$.
Technically it is more convenient to deform not commutative Hopf algebras but cocommutative ones and to start not with a Poisson–Hopf algebra (or a Poisson–Lie group [a1], which is more or less the same) but with its infinitesimal version, called a Lie bi-algebra . A Lie bi-algebra is a Lie algebra $8$ with a linear mapping $\phi : \mathfrak { g } \rightarrow \mathfrak { g } \otimes \mathfrak { g }$ such that: 1) $\phi ^ { * } : \mathfrak { g } ^ { * } \otimes \mathfrak { g } ^ { * } \rightarrow \mathfrak { g } ^ { * }$ defines a Lie algebra structure on $a ^ { x }$; and 2) $( 1 )$ is a $1$-cocycle ($8$ acts on $989$ by means of the adjoint representation). By definition, a quantization of $( g , \phi )$ is a Hopf algebra deformation of the universal enveloping algebra $U _ { G }$ such that $\delta \operatorname { lg } = \phi$, where $\delta : U _ { \mathfrak { g } } \rightarrow U _ { \mathfrak { g } } \otimes U _ { \mathfrak { g } }$ is the Poisson cobracket, defined by $\delta ( \alpha ) = \operatorname { lim } _ { h \rightarrow 0 } h ^ { - 1 } ( \Delta ( a ) - \Delta ^ { \prime } ( \alpha ) )$. Here $h$ is the deformation parameter, $\Delta$ the deformed comultiplication and $\Delta ^ { \prime }$ the opposite comultiplication.
It is not known whether every Lie bi-algebra can be quantized, and usually quantization is not unique. But in several important cases (cf. [a1], §3, §6) there exists a canonical quantization. In particular, on a Kac–Moody algebra $8$ with a fixed scalar product $( , )$ there is a canonical Lie bi-algebra structure and this bi-algebra has a canonical quantization $U _ { h } g$, as was discovered in [a3], [a4], [a5]. Let $h$ be the Cartan subalgebra of $8$, $H _ { i } \in \mathfrak { g }$ the images of the simple roots $\alpha _ { i } \in h ^ { * }$. Then $U _ { h } g$ is generated by $h$ and $X _ { i } ^ { + }$, $X$ with the following defining relations:
\begin{equation} [ \alpha _ { 1 } , \alpha _ { 2 } ] = 0 \quad \text { for } \alpha _ { 1 } , \alpha _ { 2 } \in h \end{equation}
\begin{equation} [ \alpha , X _ { i } ^ { \pm } ] = \pm \alpha _ { i } ( \alpha ) X _ { i } ^ { \pm } \quad \text { for } a \end{equation}
\begin{equation} [ X _ { i } ^ { + } , X _ { j } ^ { - } ] = 2 \delta _ { i j } h ^ { - 1 } \operatorname { sinh } ( h H _ { i } / 2 ) \end{equation}
Setting $n = 1 - A _ { i }$, $q = \operatorname { exp } h ( H _ { i } , H _ { j } ) / 2$ one has also
\begin{equation} \sum _ { k = 0 } ^ { n } ( - 1 ) ^ { k } \left( \begin{array} { l } { n } \\ { k } \end{array} \right) q ^ { - k ( n - k ) / 2 } ( X _ { i } ^ { \pm } ) ^ { k } X _ { j } ^ { \pm } \cdot ( X _ { i } ^ { \pm } ) ^ { n - k } = 0 \end{equation}
Here $( A _ { j } )$ is the Cartan matrix and $( \square _ { k } ^ { x } ) _ { q }$ is the Gauss polynomial, i.e.,
\begin{equation} \left( \begin{array} { l } { n } \\ { k } \end{array} \right) _ { q } = \frac { ( q ^ { n } - 1 ) \ldots ( q ^ { n - k + 1 } - 1 ) } { ( q ^ { k } - 1 ) \ldots ( q - 1 ) } \end{equation}
The comultiplication in $U _ { h } g$ is such that $\Delta ( \alpha ) = \alpha \otimes 1 + 1 \otimes \alpha$ for $\alpha \in h$ and
\begin{equation} \Delta ( X _ { i } ^ { \pm } ) = X _ { i } ^ { \pm } \bigotimes \operatorname { exp } ( \frac { h H _ { i } } { 4 } ) + \operatorname { exp } ( \frac { - h H _ { i } } { 4 } ) \otimes x _ { i } ^ { \pm } \end{equation}
If $8$ is a finite-dimensional simple Lie algebra (cf. Lie algebra, semi-simple), then the algebra of regular functions on the corresponding simply-connected algebraic group $k$ is isomorphic to the subalgebra of $( U _ { 9 } ) ^ { * }$ generated by the matrix elements of the finite-dimensional representations of $U _ { G }$. Therefore the subalgebra of $( U _ { k } g ) ^ { * }$ generated by the matrix elements of the finite-dimensional representations of $U _ { G }$ can be considered as the algebra of functions on a certain quantization of $k$. For instance, the quantized $SL ( n )$ (cf. above) can be obtained in this way.
There is an important notion of a quasitriangular Hopf algebra. This is a pair $( A , R )$ where $4$ is a Hopf algebra and $R$ is an invertible element of $A \otimes A$ such that $( \Delta \otimes id ) ( R ) = R ^ { 13 } R ^ { 23 }$, $( \text { id } \otimes \Delta ) ( R ) = R ^ { 13 } R ^ { 12 }$, $\Delta ^ { \prime } ( \alpha ) = R . \Delta ( \alpha ) . R ^ { - 1 }$ for $x \in A$. Here $\Delta ^ { \prime }$ is the opposite comultiplication and $R ^ { 12 }$, $R ^ { 13 }$, $R ^ { 23 }$ are defined as follows: If $R = \sum _ { i } x _ { i } \otimes y _ { i }$, where $x _ { i } , y _ { i } \in A$, then $R ^ { 12 } = \sum _ { i } x _ { i } \otimes y _ { i } \otimes 1$, $R ^ { 13 } = \sum _ { i } x _ { i } \otimes 1 \otimes y _ { i }$, $R ^ { 23 } = \sum _ { i } 1 \otimes x _ { i } \otimes y _ { i }$. If $( A , R )$ is a quasitriangular Hopf algebra, then $R$ satisfies the quantum Yang–Baxter equation (cf. also Yang–Baxter equation), i.e., $R ^ { 12 } R ^ { 13 } R ^ { 23 } = R ^ { 23 } R ^ { 13 } R ^ { 12 }$. It is known (cf. [a1], §13) that if $8$ is a finite-dimensional simple Lie algebra, then $U _ { h } g$ has a canonical quasitriangular structure, while if $8$ is an infinite-dimensional Kac–Moody algebra, then $U _ { h } g$ has an "almost quasitriangular" structure.
If $( A , R )$ is a quasitriangular Hopf algebra over $k$ and $0$ is a representation $A \rightarrow \text { Mat } ( n , k )$, then $R = ( \rho \otimes \rho ) ( R ) \in \operatorname { End } ( k ^ { n } \otimes k ^ { n } )$ satisfies the quantum Yang–Baxter equation. There is an inverse construction (cf. [a6], [a7]), which goes back to the quantum inverse-scattering method: to a matrix solution of the quantum Yang–Baxter equation satisfying a non-degeneracy condition there corresponds a Hopf algebra. Without this condition one can only construct an associative bi-algebra (the difference between a Hopf algebra and an associative bi-algebra is that in the second case there may be no antipode). This bi-algebra is generated by elements $\xi$, $1 \leq i , j \leq n$, with defining relations $R T _ { 1 } T _ { 2 } = T _ { 2 } T _ { 1 } R$, where $T _ { 1 } = T \otimes 1 \in \operatorname { End } ( k ^ { n } \otimes k ^ { n } )$, $T _ { 2 } = 1 \otimes T \in \text { End } ( k ^ { n } \otimes k ^ { n } )$, $T$ is the matrix $( t _ { j } )$, and $\Delta$ is defined by $\Delta ( t _ { j } ) = \sum _ { k } t _ { i k } \otimes t _ { k j }$.
Quasitriangular Hopf algebras are a natural tool for the quantum inverse-scattering in method ([a1], §11). On the other hand, they can be used (cf. [a8]) to construct invariants of knots (and of more general objects such as links and tangles) generalizing the Jones polynomial [a9]. More precisely, to an oriented knot $\gamma \subset R ^ { 3 }$ and a quasitriangular Hopf algebra $( A , R )$ there corresponds a central element $z _ { \gamma } \in A$.
The usual notion of a group has several versions: abstract group, Lie group, topological group, etc. The same is true for quantum groups. The quantum analogue of the notion of a compact group was introduced in [a10] (the idea is to use $C ^ { * }$-algebras instead of abstract algebras). The quantized $SU ( 2 )$ (cf. [a11], [a12]) is a typical example. The notion of a ring group (cf. , [a14]) and the equivalent notion of a Kac algebra (cf. [a15], [a16]) were introduced as an attempt to define a locally compact quantum group. However, these notions are not general enough (the axioms of , [a14], [a15] imply that the square of the antipode is the identity mapping, and therefore the quantized $SU ( 2 )$ is not a ring group).
References
| [a1] | V.G. Drinfel'd, "Quantum groups" , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , 1 , Amer. Math. Soc. (1987) pp. 798–820 Zbl 0667.16003 |
| [a2] | L.D. Faddeev, "Integrable models in ($1 + 1$)-dimensional quantum field theory" , Lectures in Les Houches, 1982 , Session 39 , Elsevier (1984) pp. 563–608 MR782509 |
| [a3] | M. Jimbo, "Quantum $R$-matrix for the generalized Toda system" Comm. Math. Phys. , 102 (1986) pp. 537–547 MR824090 |
| [a4] | M. Jimbo, "A $h$-difference analogue of $U ( g )$ and the Yang–Baxter equation" Letters Math. Phys. , 10 (1985) pp. 63–69 MR797001 |
| [a5] | V.G. Drinfel'd, "Hopf algebras and the quantum Yang–Baxter equation" Soviet Math. Dokl. , 32 (1985) pp. 254–258 Dokl. Akad. Nauk SSSR , 283 : 5 (1985) pp. 1060–1064 Zbl 0588.17015 |
| [a6] | V.V. Lyubashenko, "Hopf algebras and vector symmetries" Russian Math. Surveys , 41 : 5 (1986) pp. 153–154 Uspekhi Mat. Nauk , 41 : 5 (1986) pp. 185–186 MR0878344 Zbl 0649.16008 |
| [a7] | L.D. Faddeev, N.Yu. Reshetikhin, L.A. Takhtayan, "Quantization of Lie groups and Lie algebras" Algebra and Analysis , 1 : 1 (1989) pp. 178–206 (In Russian) MR1015339 Zbl 0677.17010 |
| [a8] | N.Yu. Reshetikhin, "Quasitriangular Hopf algebras and invariants of tangles" Algebra and Analysis , 1 : 2 (1989) pp. 169–188 (In Russian) Zbl 0715.17016 |
| [a9] | V.F.R. Jones, "A polynomial invariant for knots via von Neumann algebras" Bulletin Amer. Math. Soc. , 12 (1985) pp. 103–112 MR0766964 Zbl 0564.57006 |
| [a10] | S.L. Woronowich, "Compact matrix pseudogroups" Comm. Math. Phys. , 111 (1987) pp. 613–665 |
| [a11] | S.L. Woronowich, "Twisted SU(2) group. An example of a noncommutative differential calculus" Publ. RIMS , 23 (1987) pp. 117–181 |
| [a12] | L.L. Vaksman, Ya.S. Soibelman, "Function algebra on the quantum group SU(2)" Funct. Anal. Appl. , 22 : 3 (1988) pp. 170–181 Funksional. Anal. Prilozhen. , 22 : 3 (1988) pp. 1–14 |
| [a13a] | G.I. Kac, "Ring groups and the duality principle I" Trans. Moscow Math. Soc. , 12 (1963) pp. 291–339 Trudy Moskov. Mat. Obshch. , 12 (1963) pp. 295–301 |
| [a13b] | G.I. Kac, "Ring groups and the duality principle II" Trans. Moscow Math. Soc. , 13 (1965) pp. 94–126 Trudy Moskov. Mat. Obshch. , 13 (1965) pp. 84–113 Zbl 0162.45101 Zbl 0144.37903 |
| [a14] | G.I. Kac, L.I. Vainerman, "Nonunimodular ring groups and Hopf–von Neumann algebras" Math. USSR Sb. , 23 (1974) pp. 185–214 Mat. Sb. , 94 : 2 (1974) pp. 194–225; 335 MR0348038 |
| [a15] | M. Enock, J.-M. Schwartz, "Une dualité dans les algèbres de von Neumann" Bull. Soc. Math. France , 44 (1975) pp. 1–44 MR0442710 Zbl 0343.46044 |
| [a16] | J.-M. Schwartz, "Relations entre "ring groups" et algèbres de Kac" Bull. Sci. Math. (2) , 100 (1976) pp. 289–300 MR0473094 Zbl 0343.46043 |
Maximilian Janisch/latexlist/Algebraic Groups/Quantum groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist/Algebraic_Groups/Quantum_groups&oldid=44046