User:Maximilian Janisch/latexlist/Algebraic Groups/Maximal torus
A maximal torus of a linear algebraic group $k$ is an algebraic subgroup of $k$ which is an algebraic torus and which is not contained in any larger subgroup of that type. Now let $k$ be connected. The union of all maximal tori of $k$ coincides with the set of all semi-simple elements of $k$ (see Jordan decomposition) and their intersection coincides with the set of all semi-simple elements of the centre of $k$. Every maximal torus is contained in some Borel subgroup of $k$. The centralizer of a maximal torus is a Cartan subgroup of $k$; it is always connected. Any two maximal tori of $k$ are conjugate in $k$. If $k$ is defined over a field $k$, then there is a maximal torus in $k$ also defined over $k$; its centralizer is also defined over $k$.
Let $k$ be a reductive group defined over a field $k$. Consider the maximal subgroups among all algebraic subgroups of $k$ which are $k$-split algebraic tori. The maximal $k$-split tori thus obtained are conjugate over $k$. The common dimension of these tori is called the $k$-rank of $k$ and is denoted by $r k _ { k } G$. A maximal $k$-split torus need not, in general, be a maximal torus, that is, $r k _ { k } G$ is in general less than the rank of $k$ (which is equal to the dimension of a maximal torus in $k$). If $rk _ { k } G = 0$, then $k$ is called an anisotropic group over $k$, and if $r k _ { k } G$ coincides with the rank of $k$, then $k$ is called a split group over $k$. If $k$ is algebraically closed, then $k$ is always split over $k$. In general, $k$ is split over the separable closure of $k$.
Examples. Let $k$ be a field and let $k$ be an algebraic closure. The group $G = GL _ { \times } ( k )$ of non-singular matrices of order $12$ with coefficients in $k$ (see Classical group; General linear group) is defined and split over the prime subfield of $k$. The subgroup of all diagonal matrices is a maximal torus in $k$.
Let the characteristic of $k$ be different from 2. Let $V$ be an $12$-dimensional vector space over $k$ and $H ^ { \prime }$ a non-degenerate quadratic form on $V$ defined over $k$ (the latter means that in some basis $e _ { 1 } , \ldots , e _ { x }$ of $V$, the form $F ( x _ { 1 } e _ { 1 } + \square _ { \cdots } + x _ { x } e _ { x } )$ is a polynomial in $x _ { 1 } , \ldots , x _ { x }$ with coefficients in $k$). Let $k$ be the group of all non-singular linear transformations of $V$ with determinant 1 and preserving $H ^ { \prime }$. It is defined over $k$. Let $V _ { i }$ be the linear hull over $k$ of $e _ { 1 } , \ldots , e _ { x }$; it is a $k$-form of $V$. In $V$ there always exists a basis $f _ { 1 } , \ldots , f _ { x }$ such that
\begin{equation} F ( x _ { 1 } f _ { 1 } + \ldots + x _ { x } f _ { n } ) = x _ { 1 } x _ { n } + x _ { 2 } x _ { n } - 1 + \ldots + x _ { p } x _ { n } - p + 1 \end{equation}
where $p = n / 2$ if $12$ is even and $p = ( n + 1 ) / 2$ if $12$ is odd. The subgroup of $k$ consisting of the elements whose matrix in this basis takes the form $\| \alpha _ { i j } \|$, where $\alpha _ { \xi j } = 0$ for $i \neq j$ and 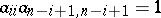 for $i = 1 , \ldots , p$, is a maximal torus in $k$ (thus the rank of $k$ is equal to the integer part of $n + 2$). In general, this basis does not belong to $V _ { i }$. However, there always is a basis $h _ { 1 } , \ldots , h _ { n }$ in $V _ { i }$ in which the quadratic form can be written as
for $i = 1 , \ldots , p$, is a maximal torus in $k$ (thus the rank of $k$ is equal to the integer part of $n + 2$). In general, this basis does not belong to $V _ { i }$. However, there always is a basis $h _ { 1 } , \ldots , h _ { n }$ in $V _ { i }$ in which the quadratic form can be written as
\begin{equation} F ( x _ { 1 } h _ { 1 } + \ldots + x _ { n } h _ { n } ) = \end{equation}
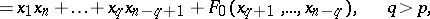 |
where $F _ { 0 }$ is a quadratic form which is anisotropic over $k$ (that is, the equation $F _ { 0 } = 0$ only has the zero solution in $k$, see Witt decomposition). The subgroup of $k$ consisting of the elements whose matrix in the basis $h _ { 1 } , \ldots , h _ { n }$ takes the form $\| \alpha _ { i j } \|$, where $\alpha _ { \xi j } = 0$ for $i \neq j$, 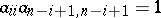 for $i = 1 , \ldots , q$ and $\alpha _ { i j } = 1$ for $i = q + 1 , \ldots , n - q$, is a maximal $k$-split torus in $k$ (so $rk _ { k } G = q$ and $k$ is split if and only if $h$ is the integer part of $n + 2$).
for $i = 1 , \ldots , q$ and $\alpha _ { i j } = 1$ for $i = q + 1 , \ldots , n - q$, is a maximal $k$-split torus in $k$ (so $rk _ { k } G = q$ and $k$ is split if and only if $h$ is the integer part of $n + 2$).
Using maximal tori one associates to a reductive group $k$ a root system, which is a basic ingredient for the classification of reductive groups. Namely, let $8$ be the Lie algebra of $k$ and let $T$ be a fixed maximal torus in $k$. The adjoint representation of $T$ in $8$ is rational and diagonalizable, so $8$ decomposes into a direct sum of weight spaces for this representation. The set of non-zero weights of this representation (considered as a subset of its linear hull in the vector space $X ( T ) \otimes _ { Z } R$, where $X ( T )$ is the group of rational characters of $T$) turns out to be a (reduced) root system. The relative root system is defined in a similar way: If $k$ is defined over $k$ and $5$ is a maximal $k$-split torus in $k$, then the set of non-zero weights of the adjoint representation of $5$ in $8$ forms a root system (which need not be reduced) in some subspace of $X ( S ) \otimes _ { Z } R$. See also Weyl group; Semi-simple group.
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) MR0251042 Zbl 0206.49801 Zbl 0186.33201 |
| [2] | A. Borel (ed.) G.D. Mostow (ed.) , Algebraic groups and discontinuous subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) MR0202512 Zbl 0171.24105 |
Comments
For $k$-forms see Form of an (algebraic) structure.
See especially the article by A. Borel in [2].
A maximal torus of a connected real Lie group $k$ is a connected compact commutative Lie subgroup $T$ of $k$ not contained in any larger subgroup of the same type. As a Lie group $T$ is isomorphic to a direct product of copies of the multiplicative group of complex numbers of absolute value 1. Every maximal torus of $k$ is contained in a maximal compact subgroup of $k$; any two maximal tori of $k$ (as any two maximal compact subgroups) are conjugate in $k$. This, in a well-known sense, reduces the study of maximal tori to the case when $k$ is compact.
Now let $k$ be a compact group. The union of all maximal tori of $k$ is $k$ and their intersection is the centre of $k$. The Lie algebra of a maximal torus $T$ is a maximal commutative subalgebra in the Lie algebra $8$ of $k$, and each maximal commutative subalgebra in $8$ can be obtained in this way. The centralizer of a maximal torus $T$ in $k$ coincides with $T$. The adjoint representation of $T$ in $8$ is diagonalizable and all non-zero weights of this representation form a root system in $X ( T ) \otimes _ { Z } R$, where $X ( T )$ is the group of characters of $T$. This is a basic ingredient for the classification of compact Lie groups.
References
| [1] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) MR0201557 Zbl 0022.17104 |
| [2] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) MR0473097 MR0473098 Zbl 0228.22013 |
| [3] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) MR0514561 Zbl 0451.53038 |
Comments
References
| [a1] | N. Bourbaki, "Groupes et algèbres de Lie" , Eléments de mathématiques , Masson (1982) pp. Chapt. 9. Groupes de Lie réels compacts MR0682756 Zbl 0505.22006 |
| [a2] | Th. Bröcker, T. Tom Dieck, "Representations of compact Lie groups" , Springer (1985) MR0781344 Zbl 0581.22009 |
Maximilian Janisch/latexlist/Algebraic Groups/Maximal torus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist/Algebraic_Groups/Maximal_torus&oldid=44037