Toda lattices
There are many Toda systems spawned by Toda's nearest neighbour linking of anharmonic oscillators on the line [a1]. A convenient container is the $2$-Toda system, first introduced and studied comprehensively in [a2]; see also [a3].
Let $M$ be a bi-infinite or semi-infinite matrix flowing as follows ($\Lambda = \Lambda _ { i , j } = \delta _ { i + 1 , j }$, the shift operator):
\begin{equation*} \frac { \partial M } { \partial x _ { n } } = \Lambda ^ { n } M , \end{equation*}
\begin{equation*} \frac { \partial M } { \partial y _ { n } } = - M ( \Lambda ^ { t } ) ^ { n }, \end{equation*}
$n = 1,2 , \dots$, with Borel decomposition
\begin{equation*} M = S _ { 1 } ^ { - 1 } S _ { 2 }, \end{equation*}
where $S _ { 1 }$ and $S _ { 2 } ^ { t }$ are lower triagonal and $\operatorname {diag} ( S _ { 1 } ) = I$.
Define
\begin{equation*} ( L _ { 1 } , L _ { 2 } ) = ( S _ { 1 } \Lambda S _ { 1 } ^ { - 1 } , S _ { 2 } \Lambda ^ { t } S _ { 2 } ^ { - 1 } ); \end{equation*}
then
\begin{equation*} \frac { \partial L _ { i } } { \partial x _ { n } } = [ ( L _ { 1 } ^ { n } ) _ { + } , L _ { i } ], \end{equation*}
\begin{equation*} \frac { \partial L _ { i } } { \partial y _ { n } } = [ ( L _ { 2 } ^ { n } ) _ { - } , L _ { i } ], \end{equation*}
$i = 1,2$; $n = 1,2 , \dots$, with eigenvectors ($[ \alpha ] = ( \alpha , \alpha ^ { 2 } / 2 , \alpha ^ { 2 } / 3 , \ldots )$, $\chi ( z ) = ( z ^ { n } ) _ { n \in \mathbf{Z} }$):
\begin{equation*} \Psi _ { 1 } ( z ) = e ^ { \sum _ { 1 } ^ { \infty } x _ { i } z ^ { i } } S _ { 1 } \chi ( z ) = \end{equation*}
\begin{equation*} = \left( \frac { e ^ { \sum _ { 1 } ^ { \infty } x _ { i } ^ { i } z ^ { i } } \tau _ { n } ( x - [ z ^ { - 1 } ] , y ) z ^ { n } } { \tau _ { n } ( x , y ) } \right) _ { n \in \mathbf{Z} } , \Psi _ { 2 } ( z ) = e ^ { \sum _ { 1 } ^ { \infty } y _ { i } z ^ { - i } } S _ { 2 } \chi ( z ) = \end{equation*}
\begin{equation*} = \left( \frac { e ^ { \sum _ { 1 }^{\infty} y _ { i } z ^ { - i } } \tau _ { n + 1 } ( x , y - [ z ] ) z ^ { n } } { \tau _ { n } ( x , y ) } \right) _ { n \in \mathbf{Z} } , ( L _ { 1 } , L _ { 2 } ) ( \Psi _ { 1 } ( z ) , \Psi _ { 2 } ( z ) ) = ( z , z ^ { - 1 } ) ( \Psi _ { 1 } ( z ) , \Psi _ { 2 } ( z ) ), \end{equation*}
\begin{equation*} \frac { \partial \Psi _ { i } } { \partial x _ { n } } = ( L ^ { n _ { 1 } } ) _ { + } \Psi _ { i } , \frac { \partial \Psi _ { i } } { \partial y _ { n } } = ( L _ { 2 } ^ { n } ) _ { - } \Psi _ { i }, \end{equation*}
$i = 1,2$; $n = 1,2 , \dots$.
Let
\begin{equation*} W _ { 1 } = S _ { 1 } e ^ { \sum _ { 1 } ^ { \infty } x _ { k } \Lambda ^ { k } }, \end{equation*}
\begin{equation*} W _ { 2 } = S _ { 2 } e ^ { \sum _ { 1 } ^ { \infty } y _ { k } ( \Lambda ^ { t } ) ^ { k } }; \end{equation*}
the crucial identity
\begin{equation*} W _ { 1 } ( x , y ) W _ { 1 } ( x ^ { \prime } , y ^ { \prime } ) ^ { - 1 } = W _ { 2 } ( x , y ) W _ { 2 } ( x ^ { \prime } , y ^ { \prime } ) ^ { - 1 } \end{equation*}
is equivalent to the bilinear identities for the tau-functions
\begin{equation*} \oint _ { z = \infty } \tau _ { n } ( x - [ z ^ { - 1 } ] , y ) \tau _ { m + 1 } ( x ^ { \prime } + [ z ^ { - 1 } ] , y ^ { \prime } ) \times \end{equation*}
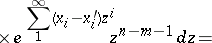 |
\begin{equation*} = \oint _ { z = \infty } \tau _ { n + 1 } ( x , y - [ z ] ) \tau _ { m } ( x ^ { \prime } , y ^ { \prime } + [ z ] ) \times \end{equation*}
\begin{equation*} \times e ^ { \sum ( y _ { i } - y _ { i } ^ { \prime } ) z ^ { - i } } z ^ { n - m - 1 } d z, \end{equation*}
which characterize the solution.
The $1$-Toda system (which can always be imbedded in the $2$-Toda system) is just the $x$-flow for $L_1$, i.e. it just involves ignoring $L_{2}$ and in effect freezing $y$ at one value. This is equivalent to the Grassmannian flag $W _ { n } \supset W _ { n + 1}$, $n \in \mathbf{Z}$, where
\begin{equation*} W _ { n } = \operatorname { span } _ { \text{C} } \left\{ \frac { \partial ^ { k } \Psi _ { 1 , n } ( x , z ) } { \partial x _ { 1 } } : k = 0,1 , \ldots \right\}, \end{equation*}
or, alternatively, it is characterized by the left-hand side of the bilinear identities $= 0$ for $n > m$ and $\mathsf{y} = \mathsf{y} ^ { \prime }$ frozen (or suppressed). The semi-infinite ($1$ or $2$) Toda system involves setting $\tau _ { - i } = 0$, $i = 1,2 , \dots$, and $\tau _ { 0 } = 1$, in which case $\tau _ { n } ( x - [ z ] , y )$ and $\tau _ { n } ( x , y + [ z ] )$ are polynomials in $z$ of degree at most $n$.
The famous triagonal Toda system — the original Toda system — is equivalent to the reduction $L _ { 1 } = L _ { 2 } = : L = L ( x - y )$ or, equivalently, $\Lambda M = M \Lambda ^ { t }$ or, equivalently, $\tau ( x , y ) = \tau ( x - y )$. In general, the $( 2 p + 1 )$-gonal Toda system $L _ { 1 } ^ { p } = L _ { 2 } ^ { p } = : L$ is equivalent to $\Lambda ^ { p } M = M ( \Lambda ^ { t } ) ^ { p }$ or, equivalently,
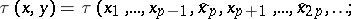 |
\begin{equation*} y _ { 1 } , \dots , \hat{y} _ { p } , \dots ; x _ { p } - y _ { p } , x _ { 2 p} - y _ { 2 p} , \dots ) \end{equation*}
The $l$-periodic $2$-Toda system is a $2$-Toda lattice such that $[ \Lambda ^ { l } , L _ { 1 } ] = [ \Lambda ^ { l } , L _ { 2 } ] = 0$. One can of course consider more than one reduction at a time. For example, the $l$-periodic triagonal Toda lattice [a4] linearizes on the Jacobian of a hyper-elliptic curve $C$ (the associated spectral curve) with the $\tau _ { n }$ being essentially theta-functions $\tau _ { n } ( t ) = \tau _ { 0 } ( t + n w )$ where $l w \equiv 0$ in $\operatorname { Jac } ( C )$, $t = x - y$, the flat coordinates on $\operatorname { Jac } ( C )$.
One can also consider in this context Toda flows going with different Lie algebras:
\begin{equation*} \dot { x } _ { i } = x _ { i } y _ { i }, \end{equation*}
\begin{equation*} \dot { y } = A x, \end{equation*}
where $x , y \in \mathbf{R} ^ { l + 1 }$, $\langle p , y \rangle = 0$, with $p A = 0$, $A$ being the Cartan matrix of Kac–Moody Lie algebras by extended Dynkin diagrams (cf. also Kac–Moody algebra). The non-periodic case involves $A$ being the Cartan matrix of a simple Lie algebra, in which case $p = 0$. The former case linearizes on Abelian varieties [a4] and the latter on "non-compact" Abelian varieties [a5].
References
| [a1] | M. Toda, "Vibration of a chain with a non-linear interaction" J. Phys. Soc. Japan , 22 (1967) pp. 431–436 |
| [a2] | K. Ueno, K. Takasaki, "Toda lattice hierarchy" Adv. Studies Pure Math. , 4 (1984) pp. 1–95 |
| [a3] | M. Adler, P. van Moerbeke, "Group factorization, moment matrices and Toda latices" Internat. Math. Research Notices , 12 (1997) |
| [a4] | M. Adler, P. van Moerbeke, "Completely integrable systems, Euclidean Lie algebras and curves; Linearization of Hamiltonians systems, Jacoby varieties and representation theory" Adv. Math. , 38 (1980) pp. 267–379 |
| [a5] | B. Konstant, "The solution to a generalized Toda lattice and representation theory" Adv. Math. , 34 (1979) pp. 195–338 |
Toda lattices. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Toda_lattices&oldid=56279