Ternary field
2020 Mathematics Subject Classification: Primary: 08-XX [MSN][ZBL]
planar ternary ring
A set $R$ with two special elements, $0$ and $1$, provided with a ternary operation $T$ satisfying:
A) $T(a,0,c)=T(0,b,c)=c$ for all $a,b,c\in R$;
B) $T(a,1,0)=T(1,a,0)=a$ for all $a\in R$;
C) if $a,b,c,d\in R$, $a\neq c$, then there is a unique $x\in R$ such that $T(x,a,b)=T(x,c,d)$;
D) if $a,b,c\in R$, then there is a unique $x\in R$ such that $T(a,b,x)=c$;
E) if $a,b,c,d\in R$, $a\neq c$, then there are unique $x,y\in R$ such that $T(a,x,y)=b$ and $T(c,x,y)=d$.
Ternary fields were introduced in [a1] for the purpose of coordinatizing arbitrary, not necessarily Desarguesian, projective planes (cf. Desargues assumption; Desargues geometry; Projective plane). Slight variations of the original definition were given in [a2] and [a3], which is followed here. Given a projective plane, fix four points in general position: $O$, $X$, $Y$, $I$, and let $A=YI\cap OX$, $B=XI\cap OY$ and $J=AB\cap XY$. For the points $\neq Y$ of $OY$ one chooses coordinates $(0,y)$ with $y$ running over a set $R$ and $0\in R$, assigning $(0,0)$ to $O$ and $(0,1)$ to $B$. The projection of $(0,x)$ from $J$ on $OX$ is given coordinates $(x,0)$, and then $Y(x,0)\cap X(0,y)=(x,y)$ (see Fig.a1). The points on $XY$ get one coordinate $(m)$, with $m\in R$, or $(\infty)$, where $\infty$ is an extra symbol $\notin R$, and the lines are coordinatized by $[m,k]$, $[b]$ or $[\infty]$, as in Fig.a2.
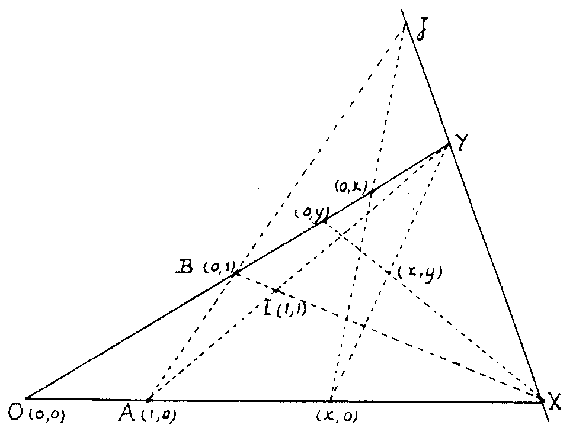
Figure: t092430a
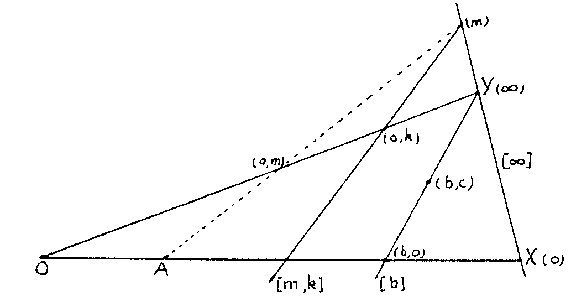
Figure: t092430b
The ternary operation $T$ on $R$ is defined by $T(a,b,c)=k$ if and only if $(b,c)$ lies on $[a,k]$. The properties A)–E) for $T$ are then consequences of the axioms for a projective plane. Conversely, any ternary field coordinatizes a projective plane. It may happen that different ternary fields coordinatize the same plane, for a different choice of basis points $O$, $X$, $Y$, $I$.
In case $R$ is finite, C) and D) are equivalent to D) and E); further, C) is then a consequence of D) and the existence of at most one $x$ as in C).
On a ternary field $(R,T)$, addition is defined by $a+b=T(1,a,b)$; with this operation $R$ is a loop with $=$ as neutral element. Multiplication is defined by $ab=T(a,b,0)$; this makes $R\setminus\{0\}$ a loop with $1$ as neutral element. $(R,T)$ is said to be linear if $T(a,b,c)=ab+c$ for all $a$, $b$, $c$. Linearity is equivalent to a very weak Desargues-type condition on triangles which are in perspective from the point $(\infty)$ (cf. Configuration, in particular Desarguesian configuration, and also Desargues assumption). Other algebraic properties of $(R,T)$, such as associativity of addition or multiplication and left or right distributivity, can also be translated into certain Desargues-type conditions. In particular, a translation plane with $XY$ as translation line, i.e., a plane in which the group of $XY$-translations is transitive on the points not on $XY$, is coordinatized by a (left) quasi-field, which is a linear ternary field with associative addition satisfying the left distributive law $a(b+c)=ab+ac$.
References
| [a1] | M. Hall, "Projective planes" Trans. Amer. Math. Soc. , 54 (1943) pp. 229–277 |
| [a2] | G. Pickert, "Projective Ebenen" , Springer (1975) |
| [a3] | D.R. Hughes, F.C. Piper, "Projective planes" , Springer (1973) |
Ternary field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ternary_field&oldid=54773