Sturm-Liouville theory
Sturm–Liouville problems (cf. Sturm–Liouville problem) have continued to provide new ideas and interesting developments in the spectral theory of operators (cf. also Spectral theory).
Consider the Sturm–Liouville differential equation on the half-line $0 \leq x < \infty$, in its reduced form
\begin{equation} \tag{a1} - y ^ { \prime \prime } + q ( x ) y = \lambda y, \end{equation}
where $\lambda$ is the complex spectral parameter and the real-valued function $q ( x )$ is assumed to be integrable over any finite subinterval of $[ 0 , \infty )$. The time-independent Schrödinger equation, at energy $\lambda$, for a particle having fixed angular momentum quantum numbers moving in a spherically symmetric potential, may be written in the form (a1) — hence there are numerous applications to quantum mechanics ([a1], [a2]).
Suppose the end-point $x = + \infty$ is a limit point. This holds in almost all applications and is valid, for example, if either $q$ is bounded or if $q$ satisfies the inequality $q ( x ) \geq - c x ^ { 2 }$ for some positive constant $c$. Let $T$ denote the second-order differential operator $T = - d ^ { 2 } / d x ^ { 2 } + q ( x )$, defined as a self-adjoint operator in $L ^ { 2 } ( 0 , \infty ),$ subject to the Dirichlet boundary condition $y ( 0 ) = 0$ (cf. also Linear ordinary differential equation of the second order). (Other boundary conditions may be considered — in general, there is a one-parameter family of boundary conditions
\begin{equation} \tag{a2} ( \operatorname { cos } \alpha ) y ( 0 ) + ( \operatorname { sin } \alpha ) y ^ { \prime } ( 0 ) = 0, \end{equation}
with the real parameter $\alpha$ varying over the interval $0 \leq \alpha < \pi$.)
The eigenvalues of the Sturm–Liouville operator $T$ may be characterized as those $\lambda \in \mathbf{R}$ for which the differential equation has a (non-trivial) solution $y ( x , \lambda )$ satisfying both the boundary condition $y ( 0 , \lambda ) = 0$ and the $L^{2}$ condition $\int _ { 0 } ^ { \infty } | y ( x , \lambda ) | ^ { 2 } d x < \infty$. The solution $y ( . , \lambda )$ will always be locally square-integrable, and the $L^{2}$ condition is a restriction on the large-$x$ asymptotic behaviour of this function. It follows, therefore, that the set of discrete points of the spectrum of $T$ (cf. also Spectrum of an operator) is governed by the asymptotic behaviour of appropriate solutions of (a1). Such considerations, which link asymptotic behaviour of solutions $y ( x , \lambda )$ of (a1) to spectral properties of the Sturm–Liouville operator $T$, may be extended to other parts of the spectrum of $T$, and provide a powerful tool of spectral analysis.
As a preliminary straightforward application of this general idea, one may use a Weyl sequence of approximate eigenfunctions of $T$ to show that if $q ( x ) \rightarrow 0$ as $x \rightarrow \infty$; then the entire positive line $[ 0 , \infty )$ belongs to the essential spectrum of $T$, the essential spectrum consisting of all points of the spectrum of $T$ apart from isolated eigenvalues. In contrast, if $q ( x ) \rightarrow + \infty$ as $x \rightarrow \infty$, then no $\lambda > 0$ belongs to the essential spectrum.
In order to carry out a more detailed spectral analysis of the Sturm–Liouville operator $T$, one has to consider the spectral measure $\mu$ associated with $T$, as well as its spectral decomposition. One of the most convenient ways to do this is through the Weyl $m$-function for $T$ ([a3], [a4], [a5], [a6]), here denoted by $m _ { 0 } ( \lambda )$ (cf. also Titchmarsh–Weyl $m$-function). The $m$-function $m _ { 0 } ( \lambda )$ for the Dirichlet Sturm–Liouville operator $- d ^ { 2 } / d x ^ { 2 } + q ( x )$ on the half-line is uniquely defined for $\operatorname { Im } \lambda > 0$ by the condition that
\begin{equation} \tag{a3} \phi ( . , \lambda ) + m _ { 0 } ( \lambda ) \theta ( . , \lambda ) \in L ^ { 2 } ( 0 , \infty ), \end{equation}
where $\phi$, $\theta$ are solutions of (a1), subject, respectively, to the conditions
\begin{equation} \tag{a4} \left\{ \begin{array} { l l } { \phi ( 0 , \lambda ) = 1 , } & { \theta ( 0 , \lambda ) = 0, } \\ { \phi ^ { \prime } ( 0 , \lambda ) = 0 , } & { \theta ^ { \prime } ( 0 , \lambda ) = 1. } \end{array} \right. \end{equation}
The function $m _ { 0 } ( \lambda )$ is an analytic function of $\lambda$ in the upper half-plane, and has strictly positive imaginary part. Such functions are called Herglotz functions, or Nevanlinna functions. (Corresponding to a general boundary condition, as given by (a2), one can define in a similar way an $m$-function $m _ { \alpha } ( \lambda )$, which is again a Herglotz function, to which the theory outlined below applies with minor modifications.)
As a Herglotz function, $m _ { 0 } ( \lambda )$ has a representation of the form ([a7]; cf. also Herglotz formula)
\begin{equation} \tag{a5} m _ { 0 } ( \lambda ) = A + \int _ { - \infty } ^ { \infty } \left( \frac { 1 } { t - \lambda } - \frac { t } { t ^ { 2 } + 1 } \right) d \rho _ { 0 } ( t ), \end{equation}
valid for all $\lambda \in \mathbf{C}$ with $\operatorname { Im } \lambda > 0$. (Actually, for a general Herglotz function, a term $B \lambda$, linear in $\lambda$ with $B > 0$, must be added on the right-hand side, but the asymptotics of $m$-functions imply that here $B = 0$ [a7].)
In (a6), $A = \operatorname { Re } m _ { 0 } ( i )$ is a positive constant and $\rho_{0} $ is the spectral function for the problem (a1) with Dirichlet boundary condition at $x = 0$. The spectral function may be taken to be non-decreasing and right continuous, in which case $\rho_{0} $ is defined by (a5) up to an additive constant, for a given $m$-function $m _ { 0 } ( \lambda )$. The measure $\mu = d \rho _ { 0 }$, defined on Borel subsets of $\mathbf{R}$, is called the spectral measure associated with the Dirichlet problem.
The Lebesgue decomposition theorem (cf. Lebesgue theorem) leads to a decomposition of the spectral measure into the sum of a part absolutely continuous with respect to Lebesgue measure and a singular part, i.e.
\begin{equation} \tag{a6} \mu = \mu _ { ac } + \mu _ { s } , \end{equation}
where $\mu _ { \text{s} }$ may be further decomposed into its singular continuous and discrete components, thus
\begin{equation} \tag{a7} \mu _ { \text{s} } = \mu _ { \text{sc} } + \mu _ { \text{d} }. \end{equation}
The Radon–Nikodým theorem implies that the absolutely continuous part 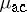 of the spectral measure may be described by means of a density function $f ( \lambda )$ given at (Lebesgue) almost all $\lambda \in \mathbf{R}$ by $f ( \lambda ) = d \rho ( \lambda ) / d \lambda$; thus, for Borel subsets $A$ of $\mathbf{R}$ one then has $\mu _ { ac } ( A ) = \int _ { A } f ( \lambda ) d \lambda$. The support of the singular component $\mu _ { \text{s} }$ will be a set $B \subseteq \mathbf{R}$ having Lebesgue measure zero. The discrete part $\mu _ { \operatorname{d} }$ is supported on the set of eigenvalues of the Sturm–Liouville operator $T$ (cf. also Eigen value). These may be characterized as the points $\lambda \in \mathbf{R}$ for which $\mu ( \{ \lambda \} ) > 0$, and alternatively as the points of discontinuity of the spectral function $\rho ( \lambda )$.
of the spectral measure may be described by means of a density function $f ( \lambda )$ given at (Lebesgue) almost all $\lambda \in \mathbf{R}$ by $f ( \lambda ) = d \rho ( \lambda ) / d \lambda$; thus, for Borel subsets $A$ of $\mathbf{R}$ one then has $\mu _ { ac } ( A ) = \int _ { A } f ( \lambda ) d \lambda$. The support of the singular component $\mu _ { \text{s} }$ will be a set $B \subseteq \mathbf{R}$ having Lebesgue measure zero. The discrete part $\mu _ { \operatorname{d} }$ is supported on the set of eigenvalues of the Sturm–Liouville operator $T$ (cf. also Eigen value). These may be characterized as the points $\lambda \in \mathbf{R}$ for which $\mu ( \{ \lambda \} ) > 0$, and alternatively as the points of discontinuity of the spectral function $\rho ( \lambda )$.
For many physical applications of the Sturm–Liouville problem (a1), the spectrum of the associated differential operator with Dirichlet boundary condition is either purely discrete (e.g. if $q ( x ) = x ^ { 2 }$), or purely absolutely continuous (e.g. if $q ( x ) \geq 0$ and $q \in L ^ { 1 } ( 0 , \infty )$), or a combination of discrete and absolutely continuous spectrum (e.g. if $q \in L ^ { 1 } ( 0 , \infty )$) and $T = - d ^ { 2 } / d x ^ { 2 } + q ( x )$ is not a positive operator). However, solution of the inverse Sturm–Liouville problem (cf. also Sturm–Liouville problem, inverse), which leads to the determination of a function $q ( x )$ from its spectral measure $\mu$,$ shows that other types of spectra, including for example combinations of absolutely continuous, singular continuous and discrete spectra, are possible. In view of the generality of types of spectral behaviour, mathematicians have sought ways of further characterizing the spectral properties of Sturm–Liouville operators which will apply to a wide range of cases. The supports of the various components of the spectral measure may be characterized in terms of the boundary behaviour of the $m$-function $m _ { 0 } ( \lambda )$. For (Lebesgue) almost-all $\lambda \in \mathbf{R}$, define the boundary value function $m_+ ( \lambda )$ by \begin{equation} \tag{a8} m _ { + } ( \lambda ) = \operatorname { lim } _ { \epsilon \rightarrow 0 + } m ( \lambda + i \epsilon ). \end{equation} Here $m_+ ( \lambda )$ exists as a finite limit for almost-all $\lambda \in \mathbf{R}$, and one defines $m _ { + } ( \lambda ) = \infty$ whenever $\operatorname { lim } _ { \epsilon \rightarrow 0 + } \operatorname { Im } m _ { + } ( \lambda ) = \infty$. Then: i) the set of all $\lambda \in \mathbf{R}$ at which $m_+ ( \lambda )$ exists and is real and finite, has zero $\mu$-measure; ii) <img src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130620/s130620114.png"/> is supported on the set of all $\lambda \in \mathbf{R}$ at which $m_+ ( \lambda )$ exists finitely, with $\operatorname{Im} m_+ ( \lambda ) > 0$; the density function for the measure <img src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130620/s130620118.png"/> is then $( 1 / \pi ) \operatorname { Im } m_+ ( \lambda )$; iii) $\mu _ { \text{s} }$ is supported on the set of all $\lambda \in \mathbf{R}$ at which $m _ { + } ( \lambda ) = \infty$. These supports can also be characterized in terms of large-$x$ asymptotics of solutions of (a1), by using the notion of subordinacy. A non-trivial solution $y ( x , \lambda )$, for given $\lambda \in \mathbf{R}$, is said to be subordinate if the norm of $y ( . , \lambda )$ in $L ^ { 2 } ( 0 , N )$ is much smaller, in the limit $N \rightarrow \infty$, than that of any other solution of (a1) that is not a constant multiple of $y ( . , \lambda )$. That is, $y ( . , \lambda )$ is subordinate if, for any other solution $v ( \, \cdot\, , \lambda )$ linearly independent of $y ( . , \lambda )$, one has (see [[#References|[a8]]], and [[#References|[a9]]] for extensions to operators with two singular end-points) \begin{equation*} \operatorname { lim } _ { N \rightarrow \infty } \frac { \int _ { 0 } ^ { N } | y ( x , \lambda ) | ^ { 2 } d x } { \int ^{N_0} | v ( x , \lambda ) | ^ { 2 } d x } = 0. \end{equation*} Then the following result holds, linking subordinacy with boundary behaviour of the $m$-function, and thereby to the spectral analysis of Sturm–Liouville operators: A subordinate solution of (a1) exists, at real spectral parameter $\lambda,$ if and only if either a) $m_+ ( \lambda )$ exists and is real and finite (in which case the solution $\phi ( . , \lambda ) + m_{ + } ( \lambda ) \theta ( . , \lambda )$ is subordinate); or b) $m _ { + } ( \lambda ) = \infty$ (in which case $\theta ( . , \lambda )$ is subordinate). In particular, the singular component $\mu _ { \text{s} }$ of the spectral measure is concentrated on the set of $\lambda \in \mathbf{R}$ at which the solution $\theta ( . , \lambda )$ is subordinate, and <img src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130620/s130620143.png"/> is concentrated on the set of $\lambda \in \mathbf{R}$ at which there is no subordinate solution. Recent developments (as of 2000) of the idea of subordinacy have led [[#References|[a10]]] to further refinements of the analysis of singular spectra, in which the [[Hausdorff dimension|Hausdorff dimension]] of the spectral support plays a significant role. The use of subordinacy and other techniques of spectral analysis have led to a deeper understanding of spectral properties for Sturm–Liouville operators in terms of the large-$x$ behaviour of solutions of the Sturm–Liouville equation (a1). Of course there still remains the problem of analyzing the large-$x$ asymptotics of solutions of (a1). However, advances in asymptotic analysis have led to the successful treatment of an ever widening class of Sturm–Liouville spectral problems. Examples of some of the most significant classes of function $q ( x )$ that can be handled in this way are as follows. ==='"`UNIQ--h-0--QINU`"'$q$ integrable plus function of bounded variation.=== (For this case plus a more general treatment of asymptotics of solutions of systems of differential equations, see [[#References|[a11]]].) Suppose one can write $q ( x ) = q _ { 1 } ( x ) + q _ { 2 } ( x )$, where $q_1$ is continuous and of bounded variation, and $q _ { 2 } ( . ) \in L ^ { 1 } ( 0 , \infty )$. Suppose also, for simplicity, that $q _ { 1 } ( x ) \rightarrow 0$ as $x \rightarrow \infty$. Then, for $\lambda > 0$, the [[WKB method|WKB method]] leads to solutions $y ( x , \lambda )$ of (a1), having the asymptotic behaviour, as $x \rightarrow \infty$, \begin{equation*} y \sim a \operatorname { cos } \int _ { c } ^ { x } ( \lambda - V _ { 1 } ( t ) ) ^ { 1 / 2 } d t + b \operatorname { sin } \int ^ { x _ { c } } ( \lambda - V _ { 1 } ( t ) ) ^ { 1 / 2 } d t. \end{equation*} Asymptotics for $\lambda < 0$ lead to exponential growth or decay of solutions. The spectrum is purely absolutely continuous for $\lambda > 0$ and purely discrete for $\lambda < 0$. ==='"`UNIQ--h-1--QINU`"'Example of eigenvalues embedded in continuous spectrum.=== ([[#References|[a12]]]) In (a1), with $\lambda = 1$, let \begin{equation*} y ( x , \lambda ) = \frac { \operatorname { sin } x } { 1 + ( 2 x - \operatorname { sin } 2 x ) ^ { 2 } }. \end{equation*} A simple calculation then shows that \begin{equation*} q ( x ) = \frac { - 8 \operatorname { sin } 2 x } { x } + 0 ( x ^ { - 2 } ) \end{equation*} as $x \rightarrow \infty$. This solution $y ( x , \lambda )$ is an eigenfunction of the Dirichlet operator $T$, with eigenvalue $\lambda = 1$. One may verify that the interval $[ 0 , \infty )$ belongs to the absolutely continuous spectrum in this example. ==='"`UNIQ--h-2--QINU`"'$q$ periodic.=== ([[#References|[a13]]]) Suppose that $q$ satisfies $q ( x + L ) = q ( x )$ for some $L > 0$. Then the absolutely continuous spectrum consists of a sequence of disjoint intervals. The detailed location of these intervals is dependent on the particular function $q$, though general results can be obtained regarding the asymptotic separation of the intervals for large $\lambda$. ==='"`UNIQ--h-3--QINU`"'$q$ almost periodic or random.=== There is an extensive literature (see, for example, [[#References|[a14]]]) on the spectral properties of $- d ^ { 2 } / d x ^ { 2 } + q ( x )$ with $q$ either almost periodic or $q$ a random function. Such problems can give rise to a singular continuous spectrum, or to a pure point spectrum which is dense in an interval. As an example of the latter phenomenon, on each interval $( n , n + 1 ]$ with $n = 0,1 , \dots$, set $q ( x ) = q _ { n }$, where the $q_n$ are constant and distributed independently for different $n$, with (say) uniform probability distribution over the interval $[ 0,1 ]$. Then, with probability $1$, the Sturm–Liouville operator $- d ^ { 2 } / d x ^ { 2 } + q ( x )$ will have eigenvalues dense in the interval $[ 0,1 ]$. ==='"`UNIQ--h-4--QINU`"'$q$ slowly oscillating.=== ([[#References|[a15]]]) A typical function of this type is given by $q ( x ) = g \operatorname { cos } \sqrt { x }$, where $g$ is a constant. The function $\cos\sqrt { x }$ oscillates more and more slowly as $x$ increases. One can show that, for almost all $g$, $- d ^ { 2 } / d x ^ { 2 } + g \operatorname { cos } \sqrt { x }$ has eigenvalues dense in the interval $[ - g , g ]$. ==='"`UNIQ--h-5--QINU`"'$q$ a sparse function.=== ([[#References|[a16]]]) A typical function of this type may be defined by $q ( x ) = \sum _ { n = 1 } ^ { \infty } f ( x - x _ { n } )$, where $f$ has compact support and the sequence $\{ x _ { n } \}$ is strongly divergent as $n \rightarrow \infty$. Such a function $q$ will give rise to a singular continuous spectrum provided $\{ x _ { n } \}$ diverges sufficiently rapidly. ==='"`UNIQ--h-6--QINU`"'$q$ slowly decaying.=== ([[#References|[a17]]]) A challenging problem in the spectral theory of Sturm–Liouville equations has been the analysis of the Dirichlet operator $- d ^ { 2 } / d x ^ { 2 } + q ( x )$ under the hypothesis that $q$ satisfy a bound for sufficiently large $x$, of the form $| q ( x ) | \leq \operatorname { const } / x ^ { \beta }$, for some $\beta > 1 / 2$. If additional conditions are imposed, for example appropriate bounds on the derivative of $q$ (assuming $q$ to be differentiable), then such functions $q$ would fall under the category "integrable plus function of bounded variation" considered above, for which a spectral analysis can be carried out. However, in the absence of further conditions on $q$, it is already clear from the example of an eigenvalue in the continuous spectrum above that one cannot prove absolute continuity of the spectrum for $\lambda > 0$. In fact, for various $q$, a dense point spectrum or singular continuous spectrum may be present. A major advance in understanding this problem has been the proof [[#References|[a17]]] that, under the hypothesis of $q$ locally integrable and $| q ( x ) | \leq \operatorname { const } / x ^ { \beta }$ ($\beta > 1 / 2$), the entire semi-interval $[ 0 , \infty )$ is contained in the absolutely continuous spectrum. Any subinterval $A$ of $[ 0 , \infty )$ will satisfy $\mu _ { \text{ac} } ( A ) > 0$; this does not exclude the possibility of a subset $B \subseteq A$ having Lebesgue measure zero with $\mu _ { s } ( B ) > 0$, and results have been obtained which further characterize the support of $\mu _ { \text{s} }$, for given $q$. Further extensions of some of these results to the more general case of $q$ square integrable have been obtained (see [[#References|[a19]]]). ==='"`UNIQ--h-7--QINU`"'Numerical approaches.=== (See, for example, [[#References|[a18]]] and references contained therein.) Sophisticated software capable of treating an increasingly wide class of spectral problems has been developed. These numerical approaches, often incorporating the use of interval analysis and leading to guaranteed error bounds for eigenvalues, have been used to investigate a variety of limit point and limit circle problems, and to estimate the $m$-function and spectral density function for a range of values of $\lambda$.
References
| [a1] | R.G. Newton, "Scattering theory of waves and particles" , Springer (1982) |
| [a2] | E. Prugovečki, "Quantum mechanics in Hilbert space" , Acad. Press (1981) |
| [a3] | E.C. Titchmarsh, "Eigenfunction expansions, Part 1" , Oxford Univ. Press (1962) |
| [a4] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) |
| [a5] | J. Chaudhury, W.N. Everitt, "On the spectrum of ordinary second order differential operators" Proc. Royal Soc. Edinburgh A , 68 (1968) pp. 95–115 |
| [a6] | M.S.P. Eastham, H. Kalf, "Schrödinger-type operators with continuous spectra" , Pitman (1982) |
| [a7] | N.I. Akhiezer, I.M. Glazman, "Theory of linear operators in Hilbert space" , Pitman (1981) |
| [a8] | D.J. Gilbert, D.B. Pearson, "On subordinacy and analysis of the spectrum of one-dimensional Schrödinger operators" J. Math. Anal. Appl. , 128 (1987) pp. 30–56 |
| [a9] | D.J. Gilbert, "On subordinacy and analysis of the spectrum of Schrödinger operators with two singular endpoints" Proc. Royal Soc. Edinburgh A , 112 (1989) pp. 213–229 |
| [a10] | S. Jitomirskaya, Y. Last, "Dimensional Hausdorff properties of singular continuous spectra" Phys. Rev. Lett. , 76 : 11 (1996) pp. 1765–1769 |
| [a11] | M.S.P. Eastham, "The asymptotic solution of linear differential systems" , Oxford Univ. Press (1989) |
| [a12] | M. Reed, B. Simon, "Methods of modern mathematical physics: Analysis of operators" , IV , Acad. Press (1978) |
| [a13] | M.S.P. Eastham, "The spectral theory of periodic differential operators" , Scottish Acad. Press (1973) |
| [a14] | L. Pastur, A. Figotin, "Spectra of random and almost periodic operators" , Springer (1991) |
| [a15] | G. Stolz, "Spectral theory for slowly oscillating potentials: Schrödinger operators" Math. Nachr. , 183 (1997) pp. 275–294 |
| [a16] | B. Simon, G. Stolz, "Operators with singular continuous spectrum: sparse potentials" Proc. Amer. Math. Soc. , 124 : 7 (1996) pp. 2073–2080 |
| [a17] | A. Kiselev, "Absolutely continuous spectrum of one-dimensional Schrödinger operators with slowly decreasing potentials" Comm. Math. Phys. , 179 (1996) pp. 377–400 |
| [a18] | "Spectral theory and computational methods of Sturm–Liouville problems" D. Hinton (ed.) P.W. Schaefer (ed.) , M. Dekker (1997) |
| [a19] | P. Deift, R. Killip, "On the absolutely continuous spectrum of one-dimensional Schrödinger operators with square-summable potentials" Comm. Math. Phys. , 203 (1999) pp. 341–347 |
Sturm–Liouville theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sturm%E2%80%93Liouville_theory&oldid=23062