Linear ordinary differential equation of the second order

An equation of the form

$$x'' + p(t)x' + q(t)x = r(t) $$

where $x(t)$ is the unknown function and $p(t)$, $q(t)$, and $r(t)$ are given functions, continuous on some interval $(a,b)$. For any real numbers $x_0$, $x_0'$, and $t_0 \in (a,b)$, there is a unique solution 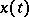of (1) defined for all 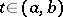with initial conditions , .

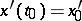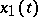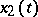If and are linearly independent solutions of the corresponding homogeneous equation

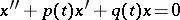(2)

and 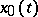is a particular solution of the inhomogeneous equation (1), then the general solution of (1) is given by the formula

where 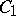and 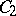are arbitrary constants. If one knows one non-zero solution 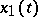of (2), then a second solution 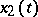of it, linearly independent of 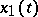, is given by the formula

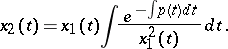If two linearly independent solutions 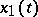and 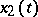of (2) are known, then a particular solution 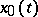of (1) can be found by the method of variation of constants.

In the study of (2) an important role is played by transformations of it to equations of other types. For example, by the change of variables 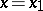, , 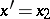equation (2) reduces to a normal system of linear equations of the second order; by a change of the unknown function,

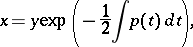equation (2) reduces to the equation 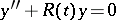, where

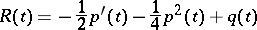is called the invariant of equation (2); by the change of variable 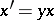, equation (2) reduces to the Riccati equation

After multiplication by

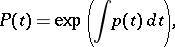equation (2) takes the self-adjoint form

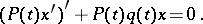Equation (2) can be integrated by quadratures only in isolated cases. The most important special types of non-integrable equations (2) give rise to special functions.

Sturm's theorem on the separation of zeros: If 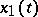and 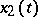are linearly independent solutions of (2) and 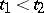are adjacent zeros of 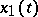, then on the interval 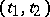there is exactly one zero of .

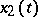Suppose that in the equations

(3)

the functions 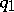and 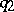are continuous and 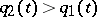on 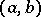. Then (the comparison theorem): If 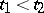are adjacent zeros of a non-zero solution of the first equation in (3), then on 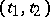there is at least one zero of any solution of the second equation in (3).

The linear boundary value problem for equation (1) can be stated as follows: Find a solution 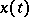of (1) that satisfies the boundary conditions

where 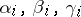are given constants and

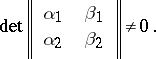The Sturm–Liouville problem for the equation

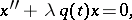where 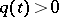is continuous on 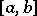, can be stated as follows: Find those values of the parameter 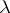for which this equation has a non-zero solution 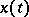satisfying the boundary conditions 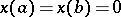. These values of 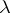are called the eigen values, and the corresponding solutions are called the eigen functions.

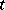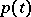If and in equation (2) are complex and the functions and 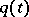are holomorphic at the point 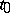, then for any numbers and 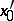there is a unique complex solution 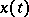of (2), holomorphic at 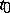, satisfying the initial conditions 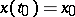, . If in the equation

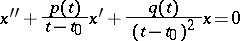(4)

the functions 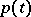and 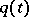are holomorphic at the point 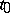and at least one of the numbers 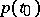, , 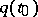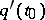is non-zero, then 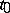is called a regular singular point for equation (4). In a neighbourhood of such a point one looks for a solution of (4) in the form of a generalized power series

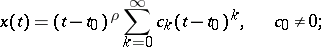(5)

here 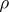is found from the defining equation

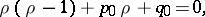where 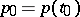and 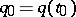. Suppose that the roots 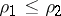of this equation are real. If 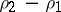is not an integer, then there are two linearly independent solutions of the form (5), for and for 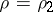. If 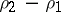is an integer, then, generally speaking, there is only one solution of the form (5), for ; the second solution has a more complicated form (see [3]–[6]).

References

[1]	L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian)
[2]	E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1947)
[3]	G. Sansone, "Ordinary differential equations" , 1–2 , Zanichelli (1948–1949) (In Italian)
[4]	P. Hartman, "Ordinary differential equations" , Birkhäuser (1982)
[5]	F. Tricomi, "Repertorium der Theorie der Differentialgleichungen" , Springer (1968)
[6]	V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian)

Comments

See also Differential equation, ordinary; Linear ordinary differential equation.

References

[a1]	E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956)
[a2]	E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17