Rayleigh-Faber-Krahn inequality
An inequality concerning the lowest eigenvalue of the Laplace operator, with Dirichlet boundary condition, on a bounded domain in ${\bf R} ^ { n }$ ($n \geq 2$).
Let $0< \lambda _ { 1 } ( \Omega ) < \lambda _ { 2 } ( \Omega ) \leq \lambda _ { 3 } ( \Omega ) \leq \dots$ be the Dirichlet eigenvalues of the Laplacian in $\Omega \subset \mathbf{R} ^ { n }$, i.e.,
\begin{equation} \tag{a1} - \Delta u = \lambda u \text { in } \Omega, \end{equation}
\begin{equation} \tag{a2} u=0 \text{ on the boundary of } \Omega. \end{equation}
(Cf. also Dirichlet boundary conditions; Dirichlet eigenvalue.) Here, $\Delta$ is the Laplace operator and $\Omega$ is an open bounded subset of ${\bf R} ^ { n }$ ($n \geq 2$). If $n = 2$, the Dirichlet eigenvalues are proportional to the square of the eigenfrequencies of an elastic, homogeneous, vibrating membrane with fixed boundary (cf. also Natural frequencies).
The Rayleigh–Faber–Krahn inequality for the membrane (i.e., $n = 2$) states that
\begin{equation} \tag{a3} \lambda _ { 1 } \geq \frac { \pi { j } _ {0,1 } ^ { 2 } } { A }, \end{equation}
where $j_{0,1} = 2.4048\dots$ is the first zero of the Bessel function of order zero (cf. also Bessel functions) and $A$ is the area of the membrane. Equality is attained in (a3) if and only if the membrane is circular. In other words, among all membranes of given area, the circle has the lowest fundamental frequency. This inequality was conjectured by Lord Rayleigh [a14], based on exact calculations for simple domains and a variational argument for near circular domains. In 1918, R. Courant [a5] proved the weaker result that among all membranes of the same perimeter $L$, the circular one yields the least lowest eigenvalue, i.e.,
\begin{equation} \tag{a4} \lambda _ { 1 } \geq \frac { 4 \pi ^ { 2 } j _ { 0,1 } ^ { 2 } } { L ^ { 2 } }, \end{equation}
with equality if and only if the membrane is circular. Rayleigh's conjecture was proven independently by G. Faber [a6] and E. Krahn [a7]. The corresponding isoperimetric inequality in dimension $n$,
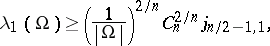 | (a5) |
was proven by Krahn [a8]. In (a5), $j_{m,1}$ is the first positive zero of the Bessel function $J _ { m }$, $| \Omega |$ is the volume of the domain and $C _ { n } = \pi ^ { n / 2 } / \Gamma ( n / 2 + 1 )$ is the volume of the $n$-dimensional unit ball. Equality is attained in (a5) if and only if $\Omega$ is a ball.
The proof of the Rayleigh–Faber–Krahn inequality rests upon two facts: a variational characterization for the lowest Dirichlet eigenvalue and the properties of symmetric decreasing rearrangements of functions. The variational characterization of the lowest eigenvalue is given by
\begin{equation} \tag{a6} \lambda _ { 1 } ( \Omega ) = \operatorname { inf } _ { u \in H _ { 0 } ^ { 1 } ( \Omega ) } \frac { \int_{\Omega} ( \nabla u ) ^ { 2 } d x } { \int _ { \Omega } u ^ { 2 } d x }. \end{equation}
Concerning decreasing rearrangements, let $\Omega$ be a measurable subset of ${\bf R} ^ { n }$, then the symmetrized domain $\Omega ^ { * }$ is a ball with the same measure as $\Omega$. If $u$ is a real-valued measurable function defined on a bounded domain $\Omega \subset \mathbf{R} ^ { n }$, its spherical decreasing rearrangement $u^*$ is a function defined on the ball $\Omega ^ { * }$ centred at the origin and having the same measure as $\Omega$, such that $u^*$ depends only on the distance from the origin, is decreasing away from the origin and is equi-measurable with $u$. See [a13], [a18], [a4] for properties of rearrangements of functions. Since the function $u$ and its spherical decreasing rearrangement are equi-measurable, their $L^{2}$-norms are the same. What Faber and Krahn actually proved is that the $L^{2}$-norm of the gradient of a function decreases under rearrangements (see [a18] for details, and also [a9] for a different approach to this fact). The fact that the $L^{2}$-norm of the gradient of a function decreases under rearrangements, combined with the variational characterization (a6), immediately gives the Rayleigh–Faber–Krahn inequality.
Isoperimetric inequalities for the lowest eigenvalue.
There are several isoperimetric inequalities for the lowest eigenvalue of boundary value problems, similar to the Rayleigh–Faber–Krahn inequality. The lowest non-trivial Neumann eigenvalue also satisfies an isoperimetric inequality. Let $0 = \mu _ { 1 } ( \Omega ) < \mu _ { 2 } ( \Omega ) \leq \mu _ { 3 } ( \Omega ) \leq \dots$ be the Neumann eigenvalues of the Laplace operator in $\Omega \subset \mathbf{R} ^ { n }$, i.e.,
\begin{equation} \tag{a7} - \Delta u = \mu u \text { in } \Omega, \end{equation}
\begin{equation} \tag{a8} \frac { \partial u } { \partial n } = 0 \text{ on the boundary of } \Omega. \end{equation}
If $n = 2$, G. Szegö [a17] proved
\begin{equation} \tag{a9} \mu _ { 2 } ( \Omega ) \leq \frac { \pi p _ { 1 } ^ { 2 } } { A }, \end{equation}
where $p _ { 1 } = 1.8412 \ldots$, with equality if and only if $\Omega$ is a circle. The corresponding result for dimension $n$,
\begin{equation} \tag{a10} \mu _ { 2 } ( \Omega ) \leq \left( \frac { 1 } { | \Omega | } \right) ^ { 2 / n } C _ { n } ^ { 2 / n } p _ { n / 2,1 } ^ { 2 }, \end{equation}
was proven by H.F. Weinberger [a19], with equality if and only if $\Omega$ is a ball. Here, $C_n$ is the volume of the unit ball in dimension $n$. In (a9) and (a10), $p_{ m , 1}$ denotes the first positive zero of the derivative of the Bessel function $J _ { m }$. For $n = 2$, Weinberger [a19] also proved
\begin{equation} \tag{a11} \frac { 1 } { \mu _ { 2 } ( \Omega ) } + \frac { 1 } { \mu _ { 3 } ( \Omega ) } \geq \frac { 2 A } { \pi p _ { 1 } ^ { 2 } }, \end{equation}
with equality if and only if $\Omega$ is a circle.
There is also an analogue of the Rayleigh–Faber–Krahn inequality for domains in spaces of constant curvature [a15]. The optimal Rayleigh–Faber–Krahn inequalities for domains in $S ^ { n }$ was proven by E. Sperner [a16].
In [a14], Lord Rayleigh also conjectured an isoperimetric inequality for the lowest eigenvalue, $\Lambda _ { 1 }$, of the clamped plate. The eigenvalue problem for the clamped plate is given by
\begin{equation*} \Delta ^ { 2 } u _ { 1 } = \Lambda _ { 1 } u _ { 1 } \text { in } \Omega \end{equation*}
with
\begin{equation*} u _ { 1 } = \left| \frac { \partial u } { \partial n } \right| = 0 \ \text{in the boundary of} \ \Omega. \end{equation*}
Here, $\Omega$ is a bounded open subset of $\mathbf{R} ^ { 2 }$. Rayleigh's conjecture for the clamped plate reads
\begin{equation} \tag{a12} \Lambda _ { 1 } ( \Omega ) \geq \Lambda _ { 1 } ( \Omega ^ { * } ), \end{equation}
where $\Omega ^ { * }$ is a ball of the same area as $\Omega$. Rayleigh's conjecture was proven by N. Nadirashvili [a12]. Equality is attained in (a12) if and only if $\Omega$ is a circle. For dimension $3$, the corresponding isoperimetric inequality was proven by M.S. Ashbaugh and R.D. Benguria [a2]. To prove the analogous result for dimensions $4$ and higher is still an open problem (as of 2000, see [a3] however).
Back in the membrane problem, if one goes beyond the lowest eigenvalue, there are several isoperimetric inequalities as well as a number of open problems. The simplest combination $\lambda _ { 2 } ( \Omega ) / \lambda _ { 1 } ( \Omega )$ satisfies the following inequality [a1]:
\begin{equation} \tag{a13} \frac { \lambda _ { 2 } ( \Omega ) } { \lambda _ { 1 } ( \Omega ) } \leq \frac { j _ { n / 2,1 } ^ { 2 } } { j _ { n / 2 - 1,1 } ^ { 2 } }, \end{equation}
in $n$ dimensions, where equality is obtained if and only if $\Omega$ is a ball. Stability results for both the Rayleigh–Faber–Krahn inequality (a3), (a4) and inequality (a13) have been obtained by A.D. Melas [a11] (in simple words, "stability" means that if $\Omega$ is convex and the appropriate left-hand side on either (a3), (a4) or (a13) is not too different from its corresponding isoperimetric value, then $\Omega$ is approximately a ball).
References
| [a1] | M.S. Ashbaugh, R.D. Benguria, "A sharp bound for the ratio of the first two eigenvalues of Dirichlet Laplacians and extensions" Ann. of Math. , 135 (1992) pp. 601–628 |
| [a2] | M.S. Ashbaugh, R.D. Benguria, "On Rayleigh's conjecture for the clamped plate and its generalization to three dimensions" Duke Math. J. , 78 (1995) pp. 1–17 |
| [a3] | M.S. Ashbaugh, R.S. Laugesen, "Fundamental tones and buckling loads of clamped plates" Ann. Scuola Norm. Sup. Pisa Cl. Sci. (Ser. IV) , XXIII (1996) pp. 383–402 |
| [a4] | C. Bandle, "Isoperimetric inequalities and applications" , Adv. Publ. Program , Pitman (1980) |
| [a5] | R. Courant, "Beweis des Satzes, dass von allen homogenen Membranen gegebenen Umfanges und gegebener Spannung die kreisförmige den tiefsten Grundton besitzt" Math. Z. , 1 (1918) pp. 321–328 |
| [a6] | G. Faber, "Beweis, dass unter allen homogenen Membranen von gleicher Fläche und gleicher Spannung die kreisförmige den tiefsten Grundton gibt" Sitzungsber. Bayer. Akad. Wiss. München, Math.-Phys. Kl. (1923) pp. 169–172 |
| [a7] | E. Krahn, "Über eine von Rayleigh formulierte Minimaleigenschaft des Kreises" Math. Ann. , 94 (1925) pp. 97–100 |
| [a8] | E. Krahn, "Über Minimaleigenschaften der Kugel in drei und mehr Dimensionen" Acta Comm. Univ. Tartu (Dorpat) , A9 (1926) pp. 1–44 (English transl.: Ü. Lumiste and J. Peetre (eds.), Edgar Krahn, 1894-1961, A Centenary Volume, IOS Press, 1994, Chap. 6, pp. 139-174) |
| [a9] | E.H. Lieb, "Existence and uniqueness of the minimizing solution of Chocquard's nonlinear equation" Stud. Appl. Math. , 57 (1977) pp. 93–105 |
| [a10] | Ü. Lumiste, J. Peetre, "Edgar Krahn, 1894-1961, A Centenary Volume" , IOS Press (1994) pp. Chap. 6 |
| [a11] | A.D. Melas, "The stability of some eigenvalue estimates" J. Diff. Geom. , 36 (1992) pp. 19–33 |
| [a12] | N.S. Nadirashvili, "Rayleigh's conjecture on the principal frequency of the clamped plate" Arch. Rational Mech. Anal. , 129 (1995) pp. 1–10 |
| [a13] | G. Pólya, G. Szegö, "Isoperimetric inequalities in mathematical physics" , Ann. of Math. Stud. , 27 , Princeton Univ. Press (1951) |
| [a14] | J.W.S. Rayleigh, "The theory of sound" , London (1894/96) pp. 339–340 (Edition: Second) |
| [a15] | E. Schmidt, "Beweis der isoperimetrischen Eigenschaft der Kugel im hyperbolischen und sphärischen Raum jeder Dimensionenzahl" Math. Z. , 49 (1943) pp. 1–109 |
| [a16] | E. Sperner, "Zur Symmetrisierung von Funktionen auf Sphären" Math. Z. , 134 (1973) pp. 317–327 |
| [a17] | G. Szegö, "Inequalities for certain eigenvalues of a membrane of given area" J. Rat. Mech. Anal. , 3 (1954) pp. 343–356 |
| [a18] | G. Talenti, "Elliptic Equations and Rearrangements" Ann. Scuola Norm. Sup. Pisa , 3 : 4 (1976) pp. 697–718 |
| [a19] | H.F. Weinberger, "An isoperimetric inequality for the $N$-dimensional free membrane problem" J. Rat. Mech. Anal. , 5 (1956) pp. 633–636 |
Rayleigh-Faber-Krahn inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rayleigh-Faber-Krahn_inequality&oldid=55546