Queue with priorities

priority queue

A priority mechanism in a queueing system discriminates customers based on their classes. Such a discrimination appears in a number of situations of everyday life and in major engineering systems, including, notably, job scheduling in manufacturing, operating systems in computers, and channel access protocols in communication networks. Clever assignment of priorities brings customer satisfaction while keeping the total workload unchanged. Extensive analysis (and optimization in operation) of queues with priority has been done by being motivated for application to specific systems as well as from theoretical interest. See also Queueing theory.

The description of the results below is based on a multi-class M/G/1 queue, namely, a queueing system with Poisson arrival processes (cf. also Poisson process), generally distributed service times, a single server, and (implicitly) an infinite capacity of the waiting room. One assumes $P$ classes of customers indexed by $p = 1 , \dots , P$. Customers of class $p$ arrive in a Poisson process at rate $\lambda _ { p }$. The mean and the second moment of the service time of each customer of class $p$ are denoted by $b _ { p }$ and $b _ { p } ^ { ( 2 ) }$, respectively. The server utilization (traffic intensity) by customers of class $p$ is given by $\rho _ { p } = \lambda _ { p } b _ { p }$, and the total server utilization by $\rho = \sum _ { p = 1 } ^ { P } \rho _ { p }$. The stability condition is given by $\rho < 1$.

For priority queues, one must distinguish pre-emptive service from non-pre-emptive service. A service discipline is said to be non-pre-emptive if, once the service to a customer is started, it is not disrupted until the whole service requirement is completed. Thus, only at the end of each service time one of the waiting customers of the highest priority class is selected for the next service. Among the customers with the same class, the tie is broken by a usual rule for non-priority queues, such as first-come-first-served (FCFS), last-come-first-served (LCFS), and random order for service (ROS). In a pre-emptive service queue, the service is given to one of the customers of the highest priority class present in the system at all times. The service is immediately pre-empted by the arrival of a customer of higher priority class. The pre-emption of service can be a model of server breakdown, where the service time for customers of higher priority class corresponds to the breakdown plus repair times.

From the viewpoint of customers, the single most important performance measure is the mean response time $\textsf{E} [ T _ { p } ]$, the expected time from the arrival to service completion. For non-pre-emptive service queues, one has $\mathsf{E} [ T _ { p } ] = \mathsf{E} [ W _ { p } ] + b _ { p }$, where $\mathsf{E} [ W _ { p } ]$ is the mean waiting time, the expected time from the arrival to service start. Thus, $\mathsf{E} [ W _ { p } ]$ is discussed for queues with non-pre-emptive service, and $\textsf{E} [ T _ { p } ]$ for queues with pre-emptive service.

If the service discipline is a non-pre-emptive service for non-priority queues, the mean waiting time of a customer of class $p$ is given by

\begin{equation*} \textsf{E}[W]_{\text{FCFS}} = \frac { 1 } { 2 ( 1 - \rho ) } \sum _ { k = 1 } ^ { P } \lambda _ { k } b _ { k } ^ { ( 2 ) }, \end{equation*}

regardless of the class $p$ (which is also the same for LCFS and ROS). If the service discipline is priority based, then $\mathsf{E} [ W _ { p } ]$ naturally depends on $p$, as presented below.

The service discipline is called work-conserving if:

a) the server is not idle when any customer is waiting;

b) the discipline does not affect the amount of service time or the arrival time of any customers. A fundamental law for a multi-class M/G/1 queue with non-pre-emptive work-conserving service is Kleinrock 's work conservation law [a3]:

\begin{equation*} \sum _ { p = 1 } ^ { P } \rho _ { p } E [ W _ { p } ] = \frac { \rho } { 2 ( 1 - \rho ) } \sum _ { p = 1 } ^ { P } \lambda _ { p } b _ { p } ^ { ( 2 ) }. \end{equation*}

This law says that the intensity-weighted sum of the mean waiting times can never change, no matter how sophisticated or elaborate the service discipline may be. If one class of customers is given favourable treatment, other classes must suffer.

In queues with absolute (or exogenous) priority, the priority classes are assigned to customers before their arrival and remain unchanged until departure. Usually, customers of class $p$ are said to have priority for service over those of class $q$ if and only if $p < q$; thus, class $1$ is the highest priority and class $P$ the lowest. Basic service disciplines with absolute priority may be classified as follows:'

non-pre-emptive: — pre-emptive: pre-emptive resume pre-emptive repeat identical pre-emptive repeat different pre-emptive loss

A classic monograph on the analysis of priority queues is [a2].

For an M/G/1 queue with non-pre-emptive priority discipline and $\rho < 1$ (unsaturated case), the mean waiting time for a customer of class $p$ is given by

\begin{equation*} \mathsf{E} [ W _ { p } ] _ { \text{NP} } = \frac { 1 } { 2 ( 1 - \sigma _ { p - 1 } ) ( 1 - \sigma _ { p } ) } \sum _ { k = 1 } ^ { P } \lambda _ { k } b _ { k } ^ { ( 2 ) }, \end{equation*}

\begin{equation*} 1 \leq p \leq P, \end{equation*}

where $\sigma _ { p } = \sum _ { k = 1 } ^ { p } \rho _ { p }$. It can be easily confirmed that this satisfies the conservation law, that 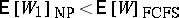and 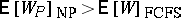, and that $\mathsf{E} [ W _ { p } ] _ { \operatorname{NP} } < \mathsf{E} [ W _ { q } ] _ { \operatorname{NP} }$ if $p < q$. In the saturated case ($\rho \geq 1$), one has

\begin{equation*} \mathsf{E} [ W _ { p } ] _ { \text{NP} } = \end{equation*}

\begin{equation*} = \frac { 1 } { 2 ( 1 - \sigma _ { p - 1 } ) ( 1 - \sigma _ { p } ) } \left[ \sum _ { k = 1 } ^ { q - 1 } \lambda _ { k } b _ { k } ^ { ( 2 ) } + ( 1 - \sigma _ { p - 1 } ) \frac { b _ { q } ^ { ( 2 ) } } { b _ { q } } \right] , 1 \leq p \leq q - 1, \end{equation*}

and $\mathsf{E} [ W _ { p } ] = \infty$ for $q \leq p \leq P$, where $q = \operatorname { inf } \{ { k } : \sigma _ { k } \geq 1 \}$. In a saturated queue with absolute priorities, there is no chance of service to customers of classes $q + 1$ through $P$ in the steady state. All the customers of classes $1$ through $q - 1$ and a portion of customers of class $q$ are served. An example of the non-pre-emptive priority discipline is the shortest job first (SJF), where the priority index (possibly continuous) is exactly the required service time.

The four types of the pre-emptive priority discipline differ as to the amount of service continued for the pre-empted customer when the server returns to him. First, a discipline is called pre-emptive resume if the pre-emption causes no loss or creation of service so that the service for the pre-empted customer is taken up where it left off. In the second type, called pre-emptive repeat identical, the original service time is repeated from the beginning regardless of the number of pre-emptions. In the third type, called pre-emptive repeat different, each repeated service time is newly sampled from the given distribution for the pre-empted customer class. Finally, if the pre-empted customer immediately disappears from the system, the discipline is called pre-emptive loss.

Many variations of the above-mentioned disciplines can be considered. For example, the service may be pre-empted only up to the specified number of times, and then continued without pre-emption till completion, or discontinued once for all. In a discretionary priority discipline, the first portion of the service time (e.g., a message header in a data transmission system) is served in pre-emptive repeat identical manner because it may contain control information, the middle portion (e.g., a user data field) is served in pre-emptive resume manner because the control information has already been acquired, and the last portion (e.g., a message trailer) is served without pre-emption because it is close to the end of service. There may be a pre-emption distance $d$ such that the pre-emption occurs only when a customer whose class is higher than the currently served one by $d$ or more classes arrives.

For an M/G/1 queue with pre-emptive resume priority discipline, the mean response time for a customer of class $p$ is given by

\begin{equation*} \mathsf{E} [ T _ { p } ] _ {\text{PR} } = \frac { 1 } { 2 ( 1 - \sigma _ { p - 1 } ) ( 1 - \sigma _ { p } ) } \sum _ { k = 1 } ^ { p } \lambda _ { k } b _ { k } ^ { ( 2 ) } + \frac { b _ { p } } { 1 - \sigma _ { p - 1 } } \end{equation*}

if $\sigma _ { p } < 1$, and $\mathsf{E} [ T _ { p } ] _ { \text{PR} } = \infty$ otherwise. Here, the response time is not affected by the customers of lower priority class. Usually, the discrimination among different classes is more distinct for the pre-emptive resume discipline than for the non-pre-emptive one. Exact analytical expressions of $\textsf{E} [ T _ { p } ]$ are also available for other types of pre-emptive priority disciplines, albeit in somewhat more complicated form [a1], [a2], [a5].

In queues with dynamic (or endogenous) priority, the priority class of each customer is determined according to the state of the system. There is no pre-assigned absolute priority. Some of the dynamic priority disciplines may be grouped as follows:'

cyclic: exhaustive gated limited time sharing: round robin processor sharing shortest remaining processing time first: — time dependent: —

In a cyclic priority (also called alternating priority or polling model) discipline, a queue of multiple classes of customers is attended by a single server in the cyclic order of class indices [a4]. The service is non-pre-emptive. The term "polling" originated with the polling data link control scheme developed in the early 1970s, in which the central computer interrogates each terminal on a multi-drop communication line to find whether it has data to transmit. The addressed terminal transmits data (service), and the computer then examines the next terminal. The same model was used for the performance evaluation of token ring local area network in the 1980s. It can also be applied to patrolling machine repairman, traffic lights at an intersection, etc. The ubiquitous application of cyclic priority discipline is not surprising, because the cyclic allocation of the server (resource) is a natural and simple way for fair arbitration to multiple users (requesters).

The three types of cyclic priority disciplines differ with respect to the rule by which the server leaves the class. In the exhaustive service discipline, the server continues to serve each class until it empties. Customers that arrive with the class currently in service are also served in the same service period for that class. In the gated service discipline, the server serves only those customers that were found in a class when it visited that class. Those that arrive during the service time are set aside to be served in the next round of visit. In the limited service discipline, at most one customer is served at each visit to a class if any are present. It is usually assumed that it takes the server some time, called the switch-over time, to move from one class to the next.

The mean waiting times are simply expressed for a symmetric queue in which the parameters of arrival, service, and switch-over processes are identical for all classes. If the mean and the variance of each switch-over time are denoted by $r$ and $\delta ^ { 2 }$, respectively, they are given by

\begin{equation*} \mathsf{E} [ W ] _ { \operatorname { exh } } = \frac { \delta ^ { 2 } } { 2 r } + \frac { P \lambda { b } ^ { ( 2 ) } + r ( P - \rho ) } { 2 ( 1 - \rho ) }, \end{equation*}

\begin{equation*} \mathsf{E} [ W ] _ { \text{gated} } = \frac { \delta ^ { 2 } } { 2 r } + \frac { P \lambda b ^ { ( 2 ) } + r ( P + \rho ) } { 2 ( 1 - \rho ) } , \mathsf{E} [ W ] _ { \text{lim} } = \frac { \delta ^ { 2 } } { 2 r } + \frac { P \lambda b ^ { ( 2 ) } + r ( P + \rho ) + P \lambda \delta ^ { 2 } } { 2 ( 1 - \rho - P \lambda r ) }, \end{equation*}

where the subscripts are dropped from $\lambda _ { p }$ and $b _ { p } ^ { ( 2 ) }$ due to symmetry. Note that

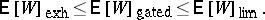However, an advantage of the limited service discipline is that each class gets a chance of service even when other classes are saturated, which is not the case for exhaustive and gated service disciplines. No closed-form expressions are available for the mean waiting times for an asymmetric system; they can be calculated through the numerical solution to a set of linear equations. However, there is a pseudo-conservation law for a queue even with mixed service disciplines:

\begin{equation*} \sum _ { p \in \text{E,G} } \rho _ { p } \mathsf{E} [ W _ { p } ] + \sum _ { p \in \text{L} } \rho _ { p } \left( 1 - \frac { \lambda _ { p } R } { 1 - \rho } \right) \mathsf{E} [ W _ { p } ] = \end{equation*}

\begin{equation*} = \frac { \rho } { 2 ( 1 - \rho ) } \sum _ { p = 1 } ^ { P } \lambda _ { p } b _ { p } ^ { ( 2 ) } + \rho \frac { \Delta ^ { 2 } } { 2 R } + \end{equation*}

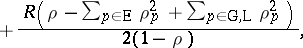where $\text{E}$, $\text{G}$, and $\operatorname{L}$ stand for the index sets of the classes with exhaustive, gated, and limited service disciplines, respectively, and $R$ and $\Delta ^ { 2 }$ are the mean and the variance of the sum of all switch-over times. If the switch-over times are zero, the pseudo-conservation law reduces to Kleinrock's conservation law. Another important performance measure for a queue with cyclic priority discipline is the mean cycle time $\mathsf{E} [ C ]$, the expected time that it takes the server to complete a cycle of visits to all classes. This is given by

\begin{equation*} \mathsf{E} [ C ] = \frac { R } { 1 - \rho } \end{equation*}

for all disciplines.

A pre-emptive service version of cyclic priority discipline may be the round robin scheduling, by which a service quantum $q$ is given cyclically to all the customers in the queue. This was studied as a model of a time sharing computer system in the late 1960s. By making $q \rightarrow 0$ in round robin scheduling, one gets the processor sharing (PS) discipline where, if $n$ customers are in the queue, each receives continuous service at the $n$th rate of the server's full capacity. In a processor sharing queue, the mean response time for a customer with service time $x$ is given by

\begin{equation*} \mathsf{E} [ T ( x ) ] _{\text{PS}} = \frac { x } { 1 - \rho }. \end{equation*}

The linear dependence of the mean response time on the customer's service time requirement is the simplest discrimination one could hope for [a3]. The unconditional mean waiting time in a processor sharing queue is given by

\begin{equation*} \mathsf{E} [ W ] _ { \operatorname {PS} } = \frac { \rho b } { 1 - \rho }, \end{equation*}

where $b$ is the mean service time averaged over all classes. Unlike the 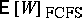, $\mathsf{E} [ W ]_{ \text{PS}}$ remains finite if the variance of the service time is infinite. Interestingly, $\mathsf{E} [ T ( x ) ]$ and $\mathsf{E} [ W ]$ in a queue with pre-emptive last-come first-served (LCFS-PR) discipline are the same as $\mathsf{E} [ T ( x ) ] _ { \operatorname{PS} }$ and $\mathsf{E} [ W ]_{ \text{PS}}$, respectively. In both disciplines, every customer starts to receive service as soon as he arrives.

The least mean response time for all work conserving disciplines is achieved by the shortest-remaining-processing-time first (SRPTF) discipline by which the customer whose remaining service time is the smallest is always placed into service. For an M/G/1 queue with SRPTF discipline, the mean response time is given by

\begin{equation*} \mathsf{E} [T]_{ \operatorname { SRPTF }} = \end{equation*}

\begin{equation*} =\lambda \int _ { 0 } ^ { \infty } \frac { \int _ { 0 } ^ { x } y [ 1 - B ( y ) ] d y } { [ 1 - \rho ( x ) ] ^ { 2 } } d B ( x ) + \int _ { 0 } ^ { \infty } \frac { 1 - B ( x ) } { 1 - \rho ( x ) } d x, \end{equation*}

where $\lambda$ is the total arrival rate, $B ( x )$ is the distribution function of the service time, and $\rho ( x ) = \lambda \int _ { 0 } ^ { x } y d B ( y )$. The optimality has been proved.

In a queue with a non-pre-emptive time-dependent priority discipline, the priority of each waiting customer changes in time. For example, the priority grows in proportion to the time he has been waiting. The growth rate depends on his class. When the server becomes free, the customer with the highest priority is chosen for the next service. In this case, it is possible to design a system with desired ratios of the mean waiting times $\mathsf{E} [ W _ { p + 1} ] / \mathsf{E} [ W _ { p } ]$, $1 \leq p \leq P - 1$, by capitalizing on the freedom of adjusting the ratios of the priority growth rates [a2], [a3]. One may also consider another time-dependent discipline, in which the priority grows as the specified deadline for service completion comes close.

References

[a1]	"Handbuch der Bedienungstheorie II" B.W. Gnedenko (ed.) D. König (ed.) , Akad. Verlag Berlin (1984) pp. Chap. 6
[a2]	N.K. Jaiswal, "Priority queues" , Acad. Press (1968)
[a3]	L. Kleinrock, "Queueing systems 2: Computer applications" , Wiley (1976) pp. Chaps. 3 and 4
[a4]	H. Takagi, "Analysis of polling systems" , MIT (1986)
[a5]	H. Takagi, "Queueing analysis 1: A foundation of performance evaluation: Vacation and priority systems" , North-Holland (1991) pp. Chap. 3