Petri net
A mathematical model of discrete dynamical systems, including data systems (parallel programs, operating systems, computers and their equipments, and computer networks), which is oriented to the qualitative analysis and synthesis of such systems (discovering deadlocks or conflict situations and bottlenecks, computer-aided synthesis of parallel programs and computer components, etc.). It was introduced by C. Petri in the 1960s. A Petri net is a set $N = (T,P,F,M_0)$, where $T$ is a finite set of symbols called transitions, $P$ is a finite set of symbols called places, $P \cap T = \emptyset$, $F$ is an incidence function: $$ F : T \times P \cup P \times T \rightarrow \{0,1\} $$ and $M_0$ is an initial marking $$ M_0 : P \rightarrow \{1,2,\ldots\} \ . $$
Informally speaking, a Petri net is a labelled oriented bipartite graph having a set of vertices $T \cup P$ (see Figure, in which $P = \{p_1,p_2,p_3\}$, $T = \{a,b,c,d\}$).
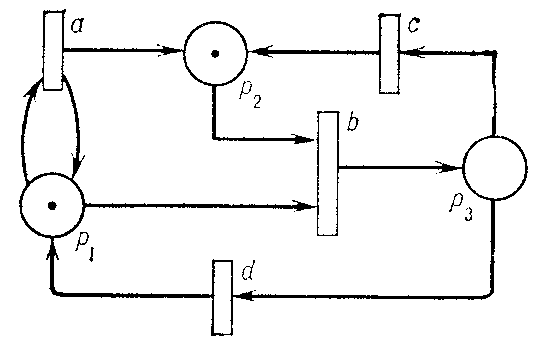
Figure: p072480a
From a place-vertex $p \in P$, represented by a circle, there runs an arc to a transition-vertex $T \in T$, represented by a rectangle, if and only if $$ F(p,t) = 1 $$ ($p$ is the input place for $t$). From a transition-vertex $t$ there runs an arc to the place-vertex $P$ if and only if $$ F(t,p) = 1 $$ ($p$ is an output place for $t$). The place $p$ is initially marked with a marking $M_0(p) \ne 0$, which is frequently represented by a corresponding number of tokens.
The dynamics of the modelled system is described in terms of the functioning of the Petri net. The net operates in discrete time by passing from marking to marking. Each marking is a function $M : P \rightarrow \{0,1,2,\ldots\}$; a change in the marking (beginning with $M_0$) is performed by a net transition. A transition $t \in T$ can fire with marking $M$ if for any $p \in P$, $$ M(p) \ge F(p,t) $$ i.e. if each input place of $t$ has at least one token. The firing of $t$ given $M$ replaces the latter by $M'$ in accordance with the following rule: for any $p \in P$, $$ M'(p) = M(p) - F(p,t) + F(t,p) $$ i.e. $t$ removes a token from each input place, and adds a token to each output place. If several transitions can fire, some one of them fires. The net halts if at some marking (a deadlock marking) none of the transitions can fire. For a given initial marking, a Petri net can generate by virtue of its indeterminate operation various sets of firing sequences. These form words over the alphabet $T$, and the set of all words generated by the Petri net is called its language. Two Petri nets are equivalent if they generate the same language.
Research on Petri nets is conducted along two lines. The mathematical theory is advanced by a formal analysis of their properties. The most interesting problems include recognizing deadlock situations, recognizing equivalence of nets from the languages they generate, evaluating complexity of nets, and comparing the expressive power for various subclasses of Petri nets and their extensions. It has been found that the deadlock problem is solvable, and the properties of the class of languages generated by Petri nets have been examined. This class is strictly contained in the class of recursively-enumerable languages and strictly includes the class of regular languages, while it partially intersects with the class of context-free languages. The second line is the use of Petri nets as the basis of models for discrete dynamical systems in information technology, economics, digital engineering, etc.
In distinction to finite automata (cf. Automaton, finite), which are used to describe global changes in the states of a system, Petri nets concentrate on local events (these correspond to transitions), local conditions (these correspond to places), and local links between events and conditions. Therefore, one can give a more adequate simulation of distributed asynchronous systems in terms of Petri nets rather than automata.
References
| [1] | J.L. Peterson, "Petri net theory and the modelling of systems" , Prentice-Hall (1981) |
| [2] | V.E. Kotov, "Petri nets" , Moscow (1986) (In Russian) |
| [3] | P.H. Starke, "Petri-Netze" , Deutsch. Verlag Wissenschaft. (1981) |
| [4] | W. Reisig, "Petri nets" , EATCS Monographs on Theoretical Computer Science , 4 , Springer (1985) Zbl 0555.68033 |
Comments
Being a basic model of parallel computations, Petri nets have been studied very extensively during recent years. There is a yearly conference on Petri nets. The best overview of currently active research is contained in the proceedings of this conference, published by Springer. The monograph [a1] contains a brief account on Petri nets; [3] is an introductory text to Petri nets. For some information on the use of Petri nets in the analysis of concurrent processes cf. e.g. [a2].
References
| [a1] | A. Salomaa, "Computation and automata" , Encyclopedia of Mathematics and Its Applications 25, Cambridge Univeristy Press (1985) Zbl 0565.68046 |
| [a2] | V.I. [V.I. Varshavskii] Varshavsky, "Self-timed control of concurrent processes" , Kluwer (1990) (Translated from Russian) Zbl 0725.94011 |
Petri net. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Petri_net&oldid=39044