Penrose tiling

Around 1975, R. Penrose discovered a pair of figures (tiles) in the plane with the following properties: i) the plane can be tiled (no gaps, no overlappings) by infinitely many copies of these two, in infinitely many (even continuously many) ways; ii) none of these tilings is periodic; iii) any finite part of such a tiling occurs infinitely often in each one of the others. See [a4], [a5].

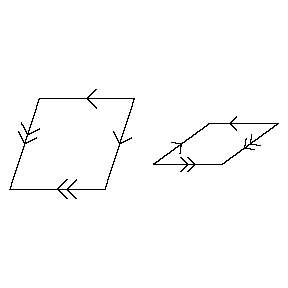
Figure: p110100a

The simplest case of a pair of such tiles is the set of arrowed rhombs (see Fig.a1; all edges have the same length, and all angles are multiples of $36^\circ$), where shape fitting is replaced by arrow fitting: there are two kinds of arrows, single and double, and the fitting condition is that adjacent tiles should have the same kind of arrows in the same direction along their common edge. Fig.a2 shows a part of a tiling with these arrowed rhombs.

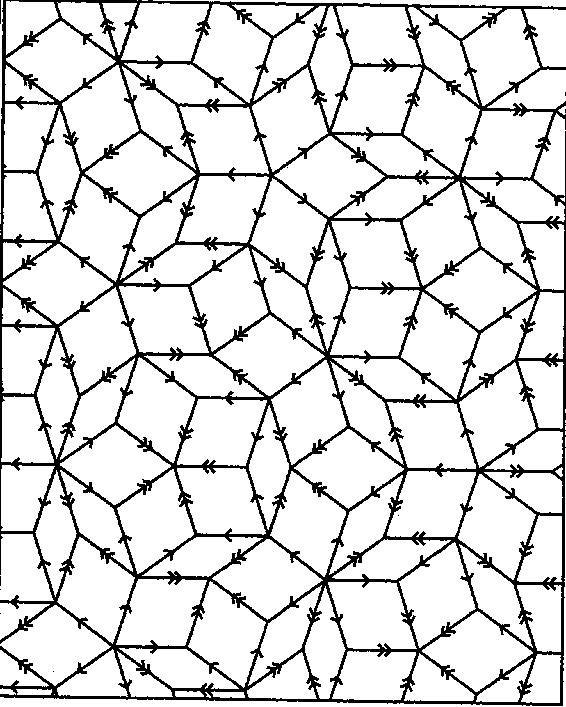
Figure: p110100b

A key to Penrose's discovery is the idea of deflation, where parts of a tiling are subdivided so as to give a new tiling with tiles similar to the old ones, but just a constant times smaller (the constant is the golden number $(-1+\sqrt5)/2$). It is not proper subdivision with these rhomb tiles, and therefore it is better to work with half rhombs, see [a3], [a6].

Three essentially different ways for generating Penrose tilings are as follows.

i) Start with a single tile and apply deflation repeatedly, each time followed by multiplication with $(1+\sqrt5)/2$. This gives tilings of bigger and bigger parts of the plane, and by König's principle one can select (non-constructively) convergent subsequences.

ii) Start with a single half rhomb and apply the inverse of deflation infinitely often. At each step there are various ways to proceed, and these options can be controlled in a simple finite oriented graph. The set of all infinite paths in that graph corresponds to the set of all Penrose tilings. See [a3], [a6].

iii) It can be proved that all Penrose tilings can be obtained as the topological duals of pentagrids: superpositions of five grids of parallel equidistant lines, obtained from one of these five by rotation over multiples of $72^\circ$ followed by translations. See [a1].

This grid presentation (or in other form, the projection method, where the tilings are obtained by projection of slices from an ordinary cubic lattice in a space of higher dimension) can be generalized at once to many kinds of grids in $n$-space. Their duals became adequate models for the quasi-crystals discovered in 1984 by D. Schechtman and others (see [a7]). The X-ray spectra of these quasicrystals correspond to the Fourier transforms of the generalized Penrose tilings (see [a2]).

References

[a1]	N.G. de Bruijn, "Algebraic theory of Penrose's non-periodic tilings of the plane" Indagationes Mathematicae , 43 (1981) pp. 38–66 Kon. Nederl. Akad. Wetensch. Proc. Ser. A , 84 (1981)
[a2]	N.G. de Bruijn, "Quasicrystals and their Fourier transform" Indagationes Mathematicae , 48 (1986) pp. 123–152 Kon. Nederl. Akad. Wetensch. Proc. Ser. A , 89 (1986)
[a3]	N.G. de Bruijn, "Updown generation of Penrose tilings" Indagationes Mathematicae N.S. , 1 (1990) pp. 201–219
[a4]	M. Gardner, "Mathematical games. Extraordinary nonperiodic tiling that enriches the theory of tiles" Scientific Amer. , 236 (1977) pp. 110–121
[a5]	R. Penrose, "Pentaplexity" Math. Intelligencer , 2 (1979) pp. 32–37
[a6]	M. Senechal, "Quasicrystals and geometry" , Cambridge Univ. Press (1995)
[a7]	P.J. Steinhardt, S. Ostlund, "The physics of quasicrystals" , World Sci. (1987)

🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️