Natural numbers object

An object in a category equipped with structure giving it properties similar to those of the set of natural numbers in the category of sets. Natural numbers objects have been most extensively studied in the context of a topos, but the definition (due to F.W. Lawvere [a6]) makes sense in any category with finite products. Lawvere's definition (like the Peano axioms for the set of natural numbers) takes the basic structure of the natural numbers object $N$ in a category $\mathcal{C}$ to consist of the zero element $o : 1 \rightarrow N$ (where $1$ denotes the terminal object of $\mathcal{C}$) and the successor mapping $s : N \rightarrow N$; the condition they are required to satisfy is that, given any diagram of the form

\begin{equation*} A \stackrel { x } { \rightarrow } B \stackrel { t } { \rightarrow } B \end{equation*}

in $\mathcal{C}$, there is a unique $f : N \times A \rightarrow B$ such that

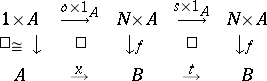commutes. If $\mathcal{C}$ is Cartesian closed (see Closed category), it is sufficient to demand this condition in the case when $A$ is the terminal object $1$. It is clear from the form of the definition that a natural numbers object, if it exists, is unique up to canonical isomorphism.

The definition is a particular case of the scheme of primitive recursion, rephrased in categorical terms; it implies that every primitive recursive function of $k$ variables is "realized" as a morphism $N ^ { k } \rightarrow N$ in $\mathcal{C}$, and that two such morphisms are equal provided the equality of the corresponding functions is provable in primitive recursive arithmetic. (For more information on the representability of recursive functions in categories, see [a5], Part III.)

Any Grothendieck topos (see Site) contains a natural numbers object; more generally, in any Cartesian closed category with countable coproducts, the countable copower of $1$ will serve as a natural numbers object. However, there are examples of toposes, such as the effective topos of M. Hyland, in which a natural numbers object exists but is not a countable copower of $1$. Natural numbers objects in toposes were studied by P. Freyd [a2]: he showed that an object $N$ in a topos, equipped with morphisms $o$ and $s$ as above, is a natural numbers object if and only if the diagram

is a coproduct and

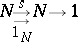is a co-equalizer, and also that these conditions are equivalent to the validity of the Peano axioms expressed in the internal logic of the topos. Further, a topos contains a natural numbers object if and only if it contains an object $A$ which is "Dedekind-infinite" in the sense that there exists a monomorphism $A \rightarrow A$ whose image is disjoint from some well-supported subobject of $A$. From the first of Freyd's characterizations, it follows that a functor between countably-cocomplete toposes which preserves finite limits and finite coproducts will preserve countable coproducts if and only if it preserves co-equalizers.

Natural numbers objects suffice not only for the recursive definition of morphisms, but also (under suitable hypotheses) for the recursive construction of objects of a topos. In particular, G. Wraith showed that the existence of a natural numbers object in a topos implies the existence of list objects: a list object over $A$ is an object $L A$ equipped with morphisms $o _ { A } : 1 \rightarrow L A$ and $s _ { A } : A \times L A \rightarrow L A$ such that, given morphisms $x : B \rightarrow C$ and $t : A \times C \rightarrow C$, there is a unique $f : L A \times B \rightarrow C$ making

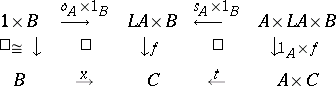commute. (Note that a natural numbers object is just a list object over $1$.) Given these, B. Lesaffre showed how to translate the usual recursive construction of free algebras (for any finitely-presented algebraic theory) into the internal logic of any topos with a natural numbers object, and P. Johnstone used the latter to construct "classifying toposes" containing generic models of such theories over any such topos. (For details of these developments, see [a4].) Conversely, A. Blass [a1] showed that the presence of a natural numbers object is necessary as well as sufficient for the construction of classifying toposes.

The existence of a natural numbers object, as a postulate, plays much the same role in topos theory as the axiom of infinity (see Infinity, axiom of) does in set theory. In classical set theory, this axiom is normally viewed as giving rise to the incompleteness phenomenon (see Gödel incompleteness theorem), via Gödel numbering of formulas; however, in the constructive logic of toposes, the picture is rather different. P. Freyd [a3] showed that (provided one assumes a meta-theory with the axiom of infinity, so that one can construct free algebras) the free topos $\mathcal{F}$ (without natural numbers object) contains a non-zero object $R$ such that the slice category $\mathcal{F} / R$ has a natural numbers object. Using this, he was able to demonstrate the existence of a "rewrite rule" which converts any sentence in higher-order intuitionistic type theory with the axiom of infinity into a sentence in the corresponding theory without the axiom of infinity, in such a way that provability is preserved and reflected.

References

[a1]	A.R. Blass, "Classifying topoi and the axiom of infinity" Algebra Univ. , 26 (1989) pp. 341–345
[a2]	P. Freyd, "Aspects of topoi" Bull. Austral. Math. Soc. , 7 (1972) pp. 1–76
[a3]	P. Freyd, "Numerals and ordinals" , unpublished manuscript (1980)
[a4]	P.T. Johnstone, G.C. Wraith, "Algebraic theories in toposes" P.T. Johnstone (ed.) R. Paré (ed.) , Indexed Categories and their Applications , Lecture Notes Math. , 661 , Springer (1978) pp. 141–242
[a5]	J. Lambek, P.J. Scott, "Introduction to higher order categorical logic" , Cambridge Univ. Press (1986)
[a6]	F.W. Lawvere, "An elementary theory of the category of sets" Proc. Nat. Acad. Sci. , 52 (1964) pp. 1506–1511