Mixed and boundary value problems for hyperbolic equations and systems
Problems of finding solutions of (systems of) partial differential equations of hyperbolic type that satisfy specific conditions on the boundaries of their domains (or on parts of it) (see Boundary conditions; Initial conditions).
A boundary value problem for (a system of) hyperbolic equations in some domain 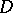 of a Euclidean space
of a Euclidean space 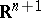 is called a mixed or initial boundary value problem if the desired solution, as well as the boundary conditions, must also satisfy initial conditions, or if the support
is called a mixed or initial boundary value problem if the desired solution, as well as the boundary conditions, must also satisfy initial conditions, or if the support 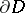 of the boundary data consists of both characteristic and non-characteristic oriented manifolds.
of the boundary data consists of both characteristic and non-characteristic oriented manifolds.
For second-order hyperbolic equations, the support of the initial data in a mixed problem is the spatially-oriented part of 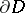 . On the time-oriented part of
. On the time-oriented part of 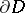 , the boundary conditions are usually of the same type as for parabolic equations (see Mixed and boundary value problems for parabolic equations and systems).
, the boundary conditions are usually of the same type as for parabolic equations (see Mixed and boundary value problems for parabolic equations and systems).
Let  be a domain in
be a domain in 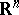 of points
of points 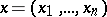 with a sufficiently smooth boundary
with a sufficiently smooth boundary 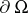 , and let
, and let
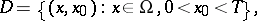 |
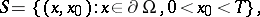 |
 |
Consider in 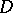 the second-order linear hyperbolic equation
the second-order linear hyperbolic equation
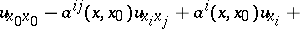 | (1) |
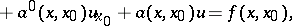 |
where summation is from 1 to  over repeated subscripts
over repeated subscripts 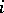 ,
, 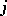 and the form
and the form 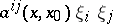 must be positive definite.
must be positive definite.
The basic mixed problems for equation (1) can be combined into the following: One has to find a solution 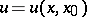 of equation (1) in
of equation (1) in 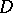 that satisfies the initial conditions
that satisfies the initial conditions
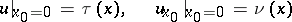 | (2) |
on 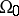 and one of the boundary conditions
and one of the boundary conditions
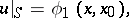 | (3) |
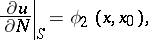 | (4) |
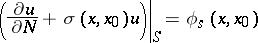 | (5) |
on 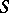 , where
, where 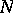 is a co-normal with respect to the operator
is a co-normal with respect to the operator 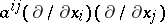 . Problems (2), (3); (2), (4); and (2), (5) are usually called the first, second and third mixed problem for equation (1), respectively.
. Problems (2), (3); (2), (4); and (2), (5) are usually called the first, second and third mixed problem for equation (1), respectively.
Under fairly general assumptions on the coefficients of (1) and on the boundary  , and also on the given functions, one can prove the existence and uniqueness of both regular and generalized solutions of all three mixed problems. The structural and differentiability properties of these solutions in the closed domain
, and also on the given functions, one can prove the existence and uniqueness of both regular and generalized solutions of all three mixed problems. The structural and differentiability properties of these solutions in the closed domain 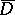 in dependence on the smoothness of the boundary have also been investigated [8]. When
in dependence on the smoothness of the boundary have also been investigated [8]. When 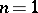 , the solutions of the mixed problems can be obtained in explicit form.
, the solutions of the mixed problems can be obtained in explicit form.
Mixed problems have been investigated for a wide class of linear and non-linear hyperbolic equations and systems (see Quasi-linear hyperbolic equations and systems). There is a satisfactory theory of mixed problems for strictly-hyperbolic equations and systems of the form
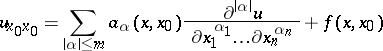 |
with initial data on the spatially-oriented part of the boundary of  lying in the plane
lying in the plane  . There has also been a successful study of mixed problems for hyperbolic equations and systems in case the supports of the initial or the boundary conditions are surfaces of degenerate type or of the order of these equations (see Degenerate partial differential equation). Most substantial results have been obtained for second-order linear equations of the form
. There has also been a successful study of mixed problems for hyperbolic equations and systems in case the supports of the initial or the boundary conditions are surfaces of degenerate type or of the order of these equations (see Degenerate partial differential equation). Most substantial results have been obtained for second-order linear equations of the form
 |
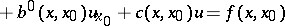 |
with coefficients satisfying the condition
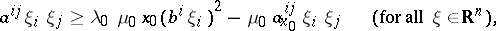 |
where 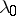 and
and 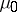 are positive constants, and especially for equations of the form
are positive constants, and especially for equations of the form
 | (6) |
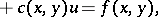 |
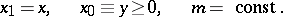 |
Mixed problems with interior or exterior boundary conditions (see Exterior and interior boundary value problems) result from mathematical models of many processes in the theory of scattering of waves on obstructions. For example, the Sommerfeld radiation condition (see Radiation conditions) results from the problem of finding a solution  of the wave equation
of the wave equation
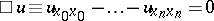 |
for all points  lying outside a bounded domain
lying outside a bounded domain 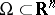 , given that the derivative of
, given that the derivative of  in the direction of the exterior normal to
in the direction of the exterior normal to 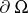 vanishes for any moment of time
vanishes for any moment of time 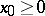 , where the initial conditions correspond to a planar wave running from infinity in the direction of the
, where the initial conditions correspond to a planar wave running from infinity in the direction of the 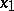 -axis.
-axis.
The basic boundary value problems for hyperbolic equations and systems are the Goursat and the Darboux–Picard problems and their multi-dimensional analogues (see Goursat problem; Cauchy characteristic problem, and also [1]).
The Goursat and Darboux–Picard problems, and various generalizations of them, have been thoroughly investigated for second-order hyperbolic equations and systems with split principal parts of the form
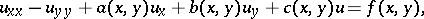 |
where  ,
, 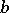 and
and  are given real
are given real 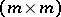 -matrices, and
-matrices, and 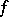 is a given and $u$ the desired
is a given and $u$ the desired 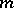 -dimensional vector. Substantial results have also been obtained for a fairly wide class of systems of second-order hyperbolic equations with non-split principal parts in the absence of parabolic degeneracy. It has been shown that the characteristic Goursat problem
-dimensional vector. Substantial results have also been obtained for a fairly wide class of systems of second-order hyperbolic equations with non-split principal parts in the absence of parabolic degeneracy. It has been shown that the characteristic Goursat problem
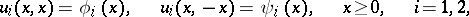 |
for the hyperbolic system
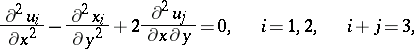 |
with two independent variables  ,
, 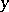 does not have a unique solution, and the effect of the lowest terms on the well-posedness of this problem has been found [3]. The influence of the nature of parabolic degeneracy on the well-posedness of both the local and the non-local boundary value problem for degenerate hyperbolic equations and systems has been thoroughly investigated [3]. This applies in particular to basic (local) boundary value problems for linear degenerate hyperbolic equations of the form
does not have a unique solution, and the effect of the lowest terms on the well-posedness of this problem has been found [3]. The influence of the nature of parabolic degeneracy on the well-posedness of both the local and the non-local boundary value problem for degenerate hyperbolic equations and systems has been thoroughly investigated [3]. This applies in particular to basic (local) boundary value problems for linear degenerate hyperbolic equations of the form
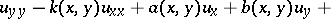 |
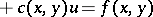 |
in bounded domains with an arbitrary piecewise-smooth boundary, and the influence of the order of non-characteristic degeneracy on the well-posedness of the Darboux problem and the non-equivalence of characteristics as supports of boundary conditions has been described (see [10]).
As to finding multi-dimensional analogues of the Darboux and Tricomi problems (see Mixed-type differential equation), much work has been done on non-local boundary value problems, and especially on problems with a shift (see [9]), for hyperbolic equations with a given condition on the characteristic parts of the boundary that connect pointwise the values of the desired solution and its (fractional) derivatives or integrals of some specific order.
Many boundary value problems with a shift that have been studied with great completeness and generality in the case of equation (1) are encompassed by the following formulation. In the domain bounded by the characteristics
 |
and the interval 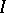 :
: 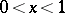 on the line
on the line 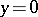 , one has to find a (sufficiently smooth) solution
, one has to find a (sufficiently smooth) solution 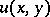 of equation (1) that satisfies on
of equation (1) that satisfies on 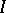 the local condition
the local condition
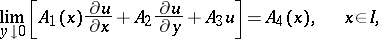 | (7) |
and on  the non-local condition
the non-local condition
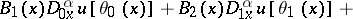 | (8) |
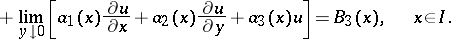 |
Here 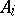 ,
, 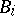 ,
, 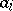 are given functions,
are given functions, 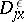 is the fractional integro-differential operator of order
is the fractional integro-differential operator of order  defined by
defined by
 |
if 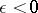 , and by
, and by
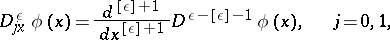 |
if 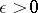 , where
, where 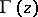 is the gamma-function,
is the gamma-function,  is the integer part of
is the integer part of  and
and 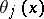 is the point of intersection of the characteristic emanating from
is the point of intersection of the characteristic emanating from 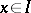 with the characteristic
with the characteristic 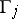 of equation (1):
of equation (1):
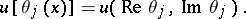 |
A detailed study has been made of boundary value problems with a shift for an equation of the form (1) which, in characteristic coordinates 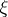 and
and 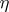 , reduces to an Euler–Darboux–Poisson equation
, reduces to an Euler–Darboux–Poisson equation
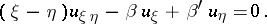 |
A special case of the problems (7), (8) is the Darboux problem, which asks for a (sufficiently smooth) solution 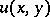 of equation (6) satisfying the (local) boundary conditions
of equation (6) satisfying the (local) boundary conditions
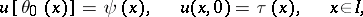 |
or
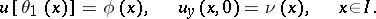 |
The condition 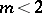 , or the Gellerstedt condition
, or the Gellerstedt condition 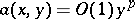 ,
, 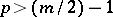 ,
, 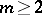 , is essential in order that the Darboux problem be well-posed (see [3], [10]).
, is essential in order that the Darboux problem be well-posed (see [3], [10]).
A qualitatively new multi-dimensional analogue of the Darboux problem is the Bitsadze problem, which in the case of the wave equation  can be posed in the following way (see [1]). In the domain
can be posed in the following way (see [1]). In the domain 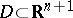 bounded by a part
bounded by a part 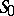 of the plane
of the plane  and the two characteristic surfaces
and the two characteristic surfaces
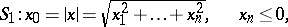 |
and
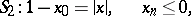 |
one has to find a solution of the equation satisfying 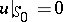 ,
, 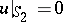 or
or 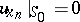 ,
, 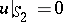 .
.
Other multi-dimensional analogues have been studied, both of the Darboux problem and of non-local boundary value problems (of the type (2), (3)) for hyperbolic equations in special domains, for which the non-characteristic part of the boundary is usually a spatially-oriented surface. Most complete results have been obtained in the case of the Euler–Darboux–Poisson equation 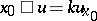 .
.
For an equation of the form
 |
much attention has been devoted to the following non-local problem. In the domain 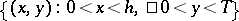 one has to find a (sufficiently smooth) solution
one has to find a (sufficiently smooth) solution 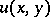 of equation
of equation
given that, for all 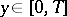 ,
,
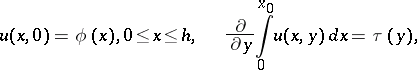 |
or
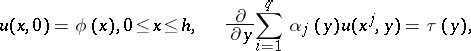 |
where 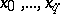 are given points in the interval
are given points in the interval 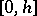 .
.
A new aspect in the theory of boundary value problems is the study of third-order hyperbolic equations of the form
 | (10) |
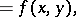 |
which lie at the basis of mathematical models for many processes and phenomena in the theory of mass or heat transfer in porous media. An extensive theory has been developed of both local and non-local linear boundary value problems for hyperbolic equations of the form (10), and in particular, an analogue of the Riemann method has been devised.
For linear symmetric hyperbolic systems of the first order (see Linear hyperbolic partial differential equation and system), a study has been made, within the limits of the theory of systems of first-order equations, of boundary value problems with admissible boundary conditions on 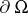 (see [6]).
(see [6]).
The Dirichlet problem is not, in general, well-posed for hyperbolic equations and systems in arbitrary domains. By methods of energy estimates and integral equations the well-posedness of this problem has been established for a wide class of second-order hyperbolic equations in special cylindrical domains.
References
| [1] | A.V. Bitsadze, "Certain classes of partial differential equations" , Moscow (1981) (In Russian) |
| [2] | V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian) |
| [3] | S. Gellerstedt, "Sur une équation linéaire aux derivées partielles du type mixte" Ark. Mat. Astr. Fys. , 25A : 29 (1937) pp. 1–23 |
| [4] | S.K. Godunov, "The equations of mathematical physics" , Moscow (1979) (In Russian) |
| [5] | T.D. Dzhuraev, "Boundary value problems for equations of mixed and mixed-composite type" , Tashkent (1979) (In Russian) |
| [6] | A.A. Dezin, "General questions in the theory of boundary value problems" , Moscow (1980) (In Russian) |
| [7] | M.M. Lavrent'ev, V.G. Romanov, V.G. Vasil'ev, "Multidimensional inverse problems for differential equations" , Springer (1970) (Translated from Russian) |
| [8] | O.A. Ladyzhenskaya, "A mixed problem for a hyperbolic equation" , Moscow (1953) (In Russian) |
| [9] | A.M. Nakhushev, "Certain boundary value problems for hyperbolic equations and for equations of mixed type" Differential Eq. , 5 : 1 (1969) pp. 37–57 Differentsial'nye Uravn. , 5 : 1 (1969) pp. 44–59 |
| [10] | A.M. Nakhushev, "Darboux's problem for degenerate hyperbolic equations" Differential Eq. , 7 : 1 (1971) pp. 41–48 Differentsial'nye Uravn. , 7 : 1 (1971) pp. 49–56 |
| [11] | M.S. Salakhitdinov, "Equations of mixed-composite type" , Tashkent (1974) (In Russian) |
| [12] | A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [13] | M.Kh. Shkhanukov, "Boundary-value problems for a third-order equation occurring in the modelling of water filtration in porous media" Differential Eq. , 18 : 4 (1982) pp. 509–517 Differentsial'nye Uravn. , 18 : 4 (1982) pp. 689–698 |
Comments
Concerning the terminology "mixed" see (the editorial comment to) Mixed and boundary value problems for parabolic equations and systems.
Mixed and boundary value problems for hyperbolic equations and systems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mixed_and_boundary_value_problems_for_hyperbolic_equations_and_systems&oldid=29417