Metric isomorphism
of two measure spaces  and
and  ; also "strict isomorphism" or "point isomorphism"
; also "strict isomorphism" or "point isomorphism"
2020 Mathematics Subject Classification: Primary: 28Axx [MSN][ZBL]
A bijective mapping  for which images and inverse images of measurable sets are measurable and have the same measure (here
for which images and inverse images of measurable sets are measurable and have the same measure (here  is some Boolean
is some Boolean  -algebra or
-algebra or  -ring of subsets of the set
-ring of subsets of the set  , called measurable, and
, called measurable, and  is a given measure on
is a given measure on  ). There is the more general notion of a (metric) homomorphism of these spaces (called also measure-preserving transformation), that is, a mapping
). There is the more general notion of a (metric) homomorphism of these spaces (called also measure-preserving transformation), that is, a mapping 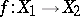 such that inverse images of measurable sets are measurable and have the same measure. For
such that inverse images of measurable sets are measurable and have the same measure. For 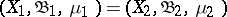 , instead of an isomorphism or a homomorphism one speaks of a (metric) automorphism or an endomorphism.
, instead of an isomorphism or a homomorphism one speaks of a (metric) automorphism or an endomorphism.
In correspondence with the usual tendency in measure theory to ignore sets of measure zero, there is (and is primarily used) a "modulo 0" version of all these ideas. For example, let 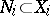 ,
, 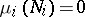 ,
, 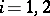 , and let
, and let 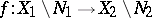 be a metric isomorphism; then it is said that
be a metric isomorphism; then it is said that 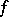 is an isomorphism modulo 0, or almost isomorphism of the original measure spaces (the stipulation "modulo 0" is often omitted).
is an isomorphism modulo 0, or almost isomorphism of the original measure spaces (the stipulation "modulo 0" is often omitted).
For a number of objects given in 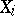 (subsets, functions, transformations, and systems of these) one can give a meaning to the assertion that under a metric isomorphism
(subsets, functions, transformations, and systems of these) one can give a meaning to the assertion that under a metric isomorphism 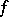 these objects transform into each other. It is then said that
these objects transform into each other. It is then said that 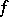 is a metric isomorphism of the corresponding objects. It is also possible to speak of their being metrically isomorphic modulo 0. This means that for certain
is a metric isomorphism of the corresponding objects. It is also possible to speak of their being metrically isomorphic modulo 0. This means that for certain 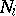 of measure zero the corresponding objects
of measure zero the corresponding objects 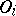 may be considered as objects
may be considered as objects 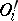 in
in 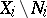 (for transformations this means that the
(for transformations this means that the 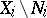 are invariant relative to these transformations, whereas for subsets and functions this makes sense for any
are invariant relative to these transformations, whereas for subsets and functions this makes sense for any 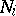 : take the intersection of the considered subsets with
: take the intersection of the considered subsets with 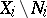 or the restrictions of the functions to
or the restrictions of the functions to 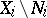 ) and that
) and that 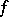 is a metric isomorphism of the objects
is a metric isomorphism of the objects 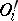 . A class of all objects metrically isomorphic modulo 0 to each other is called a (metric) type; two objects of this class are said to have the same type.
. A class of all objects metrically isomorphic modulo 0 to each other is called a (metric) type; two objects of this class are said to have the same type.
Associated with 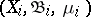 are the Hilbert spaces
are the Hilbert spaces 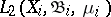 in which, in addition to the usual Hilbert space structure, there is also the operation of ordinary multiplication of functions (defined, it is true, not everywhere, since the product of
in which, in addition to the usual Hilbert space structure, there is also the operation of ordinary multiplication of functions (defined, it is true, not everywhere, since the product of 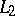 functions is not always in
functions is not always in 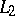 ), and the Boolean measure σ-algebras
), and the Boolean measure σ-algebras 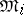 , obtained from
, obtained from 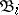 by identifying sets with symmetric difference of measure zero (that is, factorizing with respect to the ideal of sets of measure zero). A metric isomorphism
by identifying sets with symmetric difference of measure zero (that is, factorizing with respect to the ideal of sets of measure zero). A metric isomorphism 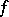 modulo 0 induces an isomorphism of the Boolean measure algebras
modulo 0 induces an isomorphism of the Boolean measure algebras 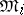 and a unitary isomorphism of the Hilbert spaces
and a unitary isomorphism of the Hilbert spaces 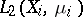 which is also multiplicative, that is, takes a product (whenever defined) to the product of the images of the multiplicands. If
which is also multiplicative, that is, takes a product (whenever defined) to the product of the images of the multiplicands. If 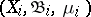 is a Lebesgue space, then the converse is true: Every isomorphism of the Boolean measure
is a Lebesgue space, then the converse is true: Every isomorphism of the Boolean measure 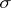 -algebras
-algebras 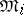 , or every multiplicative unitary isomorphism of the spaces
, or every multiplicative unitary isomorphism of the spaces 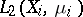 , is induced by some metric isomorphism modulo 0.
, is induced by some metric isomorphism modulo 0.
References
| [R] | V.A. Rokhlin, "On the fundamental ideas of measure theory" Mat. Sb. , 25 : 1 (1949) pp. 107–150 (In Russian) |
Comments
See also Ergodic theory for additional references. As a rule, the adjective "metric" is not anymore used and one simply speaks of an isomorphism of measure spaces, a homomorphism of measure spaces, etc.
References
| [H] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) MR0033869 Zbl 0040.16802 |
Metric isomorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Metric_isomorphism&oldid=26626