Low-dimensional topology, problems in
Many problems in two-dimensional topology (cf. Topology of manifolds) arise from, or have to do with, attempts to lift algebraic operations performed on the chain complex $\underline{\underline{C}} ( \tilde { K } )$ of a universal covering complex $\tilde { K } ^ { 2 }$ to geometric operations on the complex $K ^ { 2 }$ (here and below, "complex" means a $P L C W$-complex, i.e. a polyhedron with a $C W$-structure, see [a4] for a precise definition; for simplicity, one may think of a polyhedron): The chain complex $\underline{\underline{C}} ( \tilde { K } )$ encodes the relators of the presentation (cf. Presentation) associated to $K ^ { 2 }$ only up to commutators between relators.
A first classical example for this phenomenon occurs in the proof of the $s$-cobordism theorem (see [a7], which thus only works for manifolds of dimension $\geq 6$. In this context, J. Andrews and M. Curtis (see [a8]) asked whether the unique $5$-dimensional thickening of a compact connected $2$-dimensional complex (in short, a $2$-complex) in a $5$-dimensional piecewise-linear manifold (a PL-manifold) is a $5$-dimensional ball.
They show that this is implied by the Andrews–Curtis conjecture.
Andrews–Curtis conjecture.
This conjecture reads:
AC) any contractible finite $2$-complex $3$-deforms to a point, i.e. there exists a $3$-dimensional complex $L^3$ such that $L^3$ collapses to $K ^ { 2 }$ and to a point: $K ^ { 2 } \swarrow L ^ { 3 } \searrow \operatorname{pt}$. (Cf. [a4] for the precise notion of a collapse, which is a deformation retraction through "free faces" .)
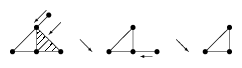
Figure: l120170a
A sequence of "elementary" collapses yielding a collapse
To a contractible finite $2$-complex there corresponds a balanced presentation (cf. Presentation) $\mathcal{P} = \langle x _ { 1 } , \dots , x _ { n } | R _ { 1 } , \dots , R _ { n } \rangle$ of the trivial group. $3$-deformations can be translated into a sequence of Andrews–Curtis moves on $\mathcal{P}$:
1) $R _ { i } \rightarrow R _ { i } ^ { - 1 }$;
2) $R _ { i } \rightarrow R _ { i } R _ { j }$, $i \neq j$;
3) $R _ { i } \rightarrow w R _ { i } w ^ { - 1 }$, $w$ any word;
4) add a generator $x_{n+1}$ and a relation $wx_{n+1}$, $w$ any word in $x _ { 1 } , \ldots , x _ { n }$.
Hence, an equivalent statement of the Andrews–Curtis conjecture is: Any balanced presentation of the trivial group can be transformed into the empty presentation by Andrews–Curtis moves.
Note that redundant relations cannot be added, since by Tietze's theorem (see [a9]) any two presentations of a group become equivalent under insertion and deletion of redundant relations and Andrews–Curtis moves.
Here are some prominent potential counterexamples to AC):
1) $\langle a , b , c | c ^ { - 1 } b c = b ^ { 2 } , a ^ { - 1 } c a = c ^ { 2 } , b ^ { - 1 } a b = a ^ { 2 } \rangle$ (E.S. Rapaport, see [a42]);
2) $\langle a , b | b a ^ { 2 } b ^ { - 1 } = a ^ { 3 } , a b ^ { 2 } a ^ { - 1 } = b ^ { 3 } \rangle$ (R.H. Crowell and R.H. Fox, see [a10], and [a11] for a generalization to an infinite series);
3) $\langle a , b | a b a = b a b , a ^ { 4 } = b ^ { 5 } \rangle$ (S. Akbulut and R. Kirby, see [a12]). This example corresponds to a homotopy $4$-sphere which is shown to be standard by a judicious addition of a $2$-, $3$-handle pair, see [a13], and [a6];
4) $\langle a , b | a = [ a ^ { p } , b ^ { q } ] , b = [ a ^ { r } , b ^ { s } ] \rangle$ (C.McA. Gordon).
An analogue of the conjecture is true in all dimensions different from $2$; in fact, the following generalization of it to non-trivial groups and keeping a subcomplex fixed holds (see [a14] for $n \geq 3$ and [a15] for $n = 1$; cf. also Homotopy type): Let $n \neq 2$; and let $f : K _ { 0 } \rightarrow K _ { 1 }$ be a simple-homotopy equivalence of connected, finite complexes, inducing the identity on the common subcomplex $L$, $n = \operatorname { max } ( \operatorname { dim } ( K _ { 0 } - L ) , \operatorname { dim } ( K _ { 1 } - L ) )$. Then $f$ is homotopic rel $L$ to a deformation $K _ { 0 } ^ { n + 1 } \searrow K _ { 1 }$ which leaves $L$ fixed throughout. A deformation is a composition of expansions and collapses; if the maximal cell dimension involved is $n$, this will be denoted by $K N L$, see [a7].
The corresponding statement for $n = 2$ is called the relative generalized Andrews–Curtis conjecture ( "generalized" because the fundamental group of $K_i$ may be non-trivial; "relative" because of the fixed subcomplex). The subcase $L = \phi$, i.e. the expectation that a simple-homotopy equivalence between finite $2$-dimensional complexes can always be replaced by a $3$-deformation, is called the generalized Andrews–Curtis conjecture, henceforth abbreviated AC'); see [a4].
Suppose $\mathcal{P} = \langle a _ { 1 } , \dots , a _ { g } | R _ { 1 } , \dots , R _ { n } \rangle$ and $\mathcal{Q} = \langle a _ { 1 } , \dots , a _ { g } | S _ { 1 } , \dots , S _ { n } \rangle$ are presentations of $\pi$ such that
D) each difference $R _ { i } S _ { i } ^ { - 1 }$ is a consequence of commutators $[ R _ { j } , R _ { k } ]$ ($1 \leq j , k \leq n$) of relators, then the corresponding $2$-dimensional complexes $K ^ { 2 }$ and $L^{2}$ are simple-homotopy equivalent. Furthermore, up to Andrews–Curtis moves the converse is true, see [a16].
Thus, in terms of presentations, AC') states that under the assumption D), $R_i$ can actually be made to coincide with $S _ { i }$ by Andrews–Curtis moves, for all $i$. Even though AC') is expected to be false, D) implies that the difference $R _ { i } S _ { i } ^ { - 1 }$ between the $i$th relators by Andrews–Curtis moves can be pushed to become a product of arbitrarily high commutators of relators, see [a17]. Furthermore, taking the one-point union not only with a finite number of $2$-spheres, but also with certain $2$-complexes of minimal Euler characteristic, eliminates any potential difference between simple-homotopy and $3$-deformations: A simple homotopy equivalence between finite connected $2$-complexes $K ^ { 2 }$, $L^{2}$ gives rise to a $3$-deformation between the one point union of $K ^ { 2 }$ (respectively, $L^{2}$) with a sufficiently large number of standard complexes of ${\bf Z} _ { 2 } \times {\bf Z} _ { 4 }$, see [a16]. For a detailed discussion on the status of the conjectures AC), AC') and relAC'), see [a4], Chap. XII.
There is a close relation between $2$-complexes and $3$-manifolds. (cf. Three-dimensional manifold): Every compact connected $3$-dimensional manifold with non-empty boundary collapses to a $2$-dimensional complex, called a spine (see [a4], Chap. I, §2.2), and thus determines a $3$-deformation class of $2$-complexes. A counterexample to AC) which is a $3$-manifold with spine $K ^ { 2 }$ would disprove the $3$-dimensional Poincaré conjecture (cf. Three-dimensional manifold)
Zeeman conjecture.
This prominent conjecture on $2$-complexes actually implies the $3$-dimensional Poincaré conjecture. The Zeeman conjecture states that (see [a23]):
Z) if $K ^ { 2 }$ is a compact contractible $2$-dimensional complex, then $K ^ { 2 } \times I \searrow \operatorname{pt}$, where $I$ is an interval. Note that Z) also implies AC), as $K ^ { 2 } \nearrow K ^ { 2 }\times I \searrow \operatorname {pt}$ would be a $3$-deformation. Examples which fulfil $K ^ { 2 } \times I \searrow \operatorname{pt}$ are the dunce hat, Bing's house and the house with one room, see [a4]. However, $K ^ { 2 } \times I \searrow \operatorname{pt}$ is not even established (as of 1999) for most of the standard $2$-complexes of presentations $\langle a , b | a ^ { p } b ^ { q } , a ^ { r } b ^ { s } \rangle$ where $p s - q r = \pm 1$, even though these are Andrews–Curtis equivalent to the empty presentation.
As for AC), there is a straightforward generalization to non-trivial groups; the generalized Zeeman conjecture:
Z') $K ^ { 2 } / \searrow L ^ { 2 }$ implies $K ^ { 2 } \times I \searrow L ^ { 2 }$ or $L ^ { 2 } \times I \searrow K ^ { 2 }$. Of course, Z') implies both Z) and AC'). It is open (as of 1999) whether AC') implies Z'), but given a $3$-deformation between finite $2$-complexes $K ^ { 2 }/ \stackrel { 3 } { \searrow } L ^ { 2 }$, then $K ^ { 2 }$ can be expanded by a sequence of $2$-expansions to a $2$-complex $K ^ { \prime 2 } \searrow K ^ { 2 }$ such that $K ^ { \prime 2 } \times I \searrow \operatorname{pt}$, see [a18].
In the special case of expansion of a single $3$-ball, followed by a $3$-collapse, $K ^ { 2 } \nearrow K ^ { 2 } \cup _ { B ^ { 2 } } B ^ { 3 } \searrow L ^ { 2 }$, it is true that $K ^ { 2 } \times I \searrow L ^ { 2 }$, see [a19], [a20], [a21]. This can be viewed as a first step in proving Z') modulo AC'), as every $3$-deformation between finite $2$-complexes can be replaced by one where each $3$-ball is transient, i.e. is collapsed (in general from a different free face) immediately after its expansion, see [a22]. For $L ^ { 2 } = \operatorname {pt}$, this method is called collapsing by adding a cell and works for all above-mentioned examples for $K ^ { 2 } \times I \searrow \operatorname{pt}$.
A second general method for collapsing $K ^ { 2 } \times I$ was proposed by A. Zimmermann (see [a24]) and is called prismatic collapsing. At first one gets rid of the $3$-dimensional part of $K ^ { 2 } \times I$ as follows: For each $2$-cell $C ^ { 2 }$ of $K ^ { 2 }$ one collapses $C ^ { 2 } \times I$ to the union of $\partial C ^ { 2 } \times I$ and a $2$-cell $C ^ { * } \subset C ^ { 2 } \times I$ such that the direct product projection maps $\operatorname { lnt } C ^ { * }$ onto $\operatorname { lnt } C ^ { 2 }$ homeomorphically. Then one looks for a collapse of the resulting $2$-complex.
One may say that prismatic collapsing is a very rough method, but exactly this roughness allows one to give an algebraic criterion for the prismatic collapsibility of $K ^ { 2 } \times I$: Attaching mappings for $2$-cells of $K ^ { 2 }$ have to determine a basis-up-to-conjugation in the free fundamental group of the $1$-dimensional skeleton (see [a7]) of $K ^ { 2 }$.
Z) becomes true if one admits multiplication of $K ^ { 2 }$ by the $n$-fold product 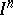 of $I$: For each contractible $K ^ { 2 }$ there exists an integer $n$ such that $K ^ { 2 } \times I ^ { n } \searrow \operatorname{pt}$, see [a19], [a20]. In fact, $n = 6$ suffices for all $K ^ { 2 }$, see [a25]. It is surprising that there is such a large gap between the presently (1999) known ($n = 6$) and Zeeman's conjectured ($n = 1$) values of $n$.
of $I$: For each contractible $K ^ { 2 }$ there exists an integer $n$ such that $K ^ { 2 } \times I ^ { n } \searrow \operatorname{pt}$, see [a19], [a20]. In fact, $n = 6$ suffices for all $K ^ { 2 }$, see [a25]. It is surprising that there is such a large gap between the presently (1999) known ($n = 6$) and Zeeman's conjectured ($n = 1$) values of $n$.
On the other hand, a generalization of Z) to higher-dimensional complexes is false, since for any $n > 2$ there exists a contractible complex $K ^ { n }$ of dimension $n$ such that $K ^ { n } \times 1$ is not collapsible, see [a26]. The proof of non-collapsibility is based on a very specific (one may say "bad" ) local structure of $K ^ { n }$. So, the idea to investigate Z) for $2$-dimensional polyhedra with a "nice" local structure (such polyhedra are called special) seems to be very promising.
In fact, if $K ^ { 2 }$ is a special spine of a homotopy $3$-ball $M ^ { 3 }$, then $K ^ { 2 } \times I$ collapses onto a homeomorphic copy of $M ^ { 3 }$, see [a27]. It follows that Z) is true for all special spines of a genuine $3$-ball and that for special spines of $3$-manifolds, Z) is equivalent to the $3$-dimensional Poincaré conjecture. Surprisingly, for special polyhedra that cannot be embedded in a $3$-manifold, Z) turns out to be equivalent to AC) (see [a28]), so that for special polyhedra, Z) is equivalent to the union of AC) and the $3$-dimensional Poincaré conjecture.
$\operatorname{Wh} ^ { * }$-question.
Another situation where dimension $2$ presents a severe difficulty in passing from chain complexes to geometry concerns the Whitehead group and the Whitehead torsion of a pair $( K , L )$, where $L$ is a strong deformation retraction of $K$ (cf. Whitehead group, Whitehead torsion). All elements of $\operatorname{Wh} ( \pi )$ can be realized by $\operatorname { dim } K = 3$. Let $\operatorname{Wh} ^ { * } ( \pi ) \subseteq \operatorname{Wh} ( \pi )$ be the set of those torsion values that can be realized by a $2$-dimensional extension, i.e. $\operatorname { dim } ( K - L ) \leq 2$. The $\operatorname{Wh} ^ { * }$-question is whether $\operatorname{Wh} ^ { * } ( \pi ) \neq \{ 0 \}$ can happen; see [a4]. If so, another related question is whether $\operatorname{ Wh} ^ { * } ( \pi )$ is a subgroup.
A famous result of O.S. Rothaus is that there exist examples $\tau \in \operatorname{Wh} ( \pi )$ for dihedral groups $\pi$ with $\tau \notin \operatorname{Wh} ^ { * } ( \pi )$; see [a29]. This result was the basis for work by M.M. Cohen [a26] on the generalization of Z) to higher dimensions.
Whitehead's asphericity question.
A $2$-complex $K$ is called aspherical if its second homotopy group $\pi_2 ( K )$ is trivial (or equivalently, if all $\pi _ { n } ( K )$ for $n \geq 2$ are trivial). J.H.C. Whitehead asked, (see [a30]), whether subcomplexes of aspherical $2$-complexes are themselves aspherical. An affirmative answer to this question is called the Whitehead conjecture:
WH) A subcomplex $K$ of an aspherical $2$-complex $L$ is aspherical.
A lot of work has already been done in trying to solve this conjecture and there are about six false results in the literature which would imply WH).
WH) is known to be true if $K$ has at most one $2$-cell and also in the case where $\pi_1 ( L )$ is either finite, Abelian or free, see [a31]. If $K$ is a subcomplex of an aspherical $2$-complex, then one can show that the second homology of the covering $\overline { K } \rightarrow K$ corresponding to the commutator subgroup is trivial. In fact, J.F. Adams has shown [a32] that $K$ has an acyclic regular covering $K ^ { * } \rightarrow \overline { K } \rightarrow K$ (i.e. $H _ { 2 } ( K ^ { * } ) = H _ { 1 } ( K ^ { * } ) = 0$). A counterexample to WH) can thus be covered by an acyclic complex, but not by a contractible one.
In any counterexample $K \subset L$ to WH), the kernel of the inclusion induced mapping $\pi _ { 1 } ( K ) \rightarrow \pi _ { 1 } ( L )$ has a non-trivial, finitely generated, perfect subgroup, [a33].
J. Howie has shown [a34] that if WH) is false, then there exists a counterexample $K \subset L$ satisfying either
a) $L$ is finite and contractible, and $K = L - e$ for some $2$-cell $e$ of $L$; or
b) $L$ is the union of an infinite ascending chain of finite non-aspherical subcomplexes $K = K _ { 0 } \subset K _ { 1 } \subset \ldots$ such that each inclusion mapping is nullhomotopic.
This result has been sharpened by E. Luft, who showed that if WH) is false, then there must even exist an infinite counterexample of type b).
Let $\mathcal{P} = \langle x _ { 1 } , \dots , x _ { g } | R _ { 1 } , \dots , R _ { n } \rangle$ be a finite presentation where each relator is of the form $x _ { i } = x _ { j } x _ { k } x _ { j } ^ { - 1 }$. Such a presentation may be represented by a graph $T _ { \mathcal{P} }$ in the following way: For each generator $x_{i}$ of $\mathcal{P}$, define a vertex labelled $i$ and for each relator $x _ { i } = x _ { j } x _ { k } x _ { j } ^ { - 1 }$ define an edge oriented from the vertex $i$ to the vertex $k$ labelled by $j$. If $T _ { \mathcal{P} }$ is a tree, then $\mathcal{P}$ or $T _ { \mathcal{P} }$ or the standard-$2$-complex $K _ { \mathcal{P} }$ modelled on $\mathcal{P}$ is called a labelled oriented tree.
Now Howie showed [a34] that if the Andrews–Curtis conjecture is true and all labelled oriented trees are aspherical, then there are no counterexamples of type a) to WH). Conversely, if there are no counterexamples of type a) to WH), then all labelled oriented trees are aspherical, which is easy to see since adding an extra relator $x _ { 1 } = 1$ to a labelled oriented tree yields a balanced presentation of the trivial group and hence a contractible complex.
So the finite case of WH) can be reduced to the study of the asphericity of labelled oriented trees. Every knot group has a labelled oriented tree presentation (the Wirtinger presentation, see, e.g., [a6]) and by a theorem of C.D. Papakyriakopoulos, [a36], it is known that these labelled oriented trees are aspherical. Every labelled oriented tree satisfying the small cancellation conditions $C ( 4 )$, $T ( 4 )$ or a more refined curvature condition such as the weight or cycle test, [a37], is aspherical. Apart from that, there are not many classes of aspherical labelled oriented trees known: Howie, [a35], shows the asphericity of labelled oriented trees of diameter at most $3$ and G. Huck and S. Rosebrock have two other classes of aspherical labelled oriented trees satisfying certain conditions on the relators.
An overview on WH), where further aspects of this conjecture are treated, can be found in [a4], Chap. X.
Wall's domination problem.
Given a CW-complex, it is natural to ask whether it can be replaced by a simpler one having the same homotopy type. Questions of this kind were first considered by J.H.C. Whitehead, who posed in particular the question: When is a CW-complex homotopy equivalent to a finite dimensional one? In [a38], C.T.C. Wall answered this by giving an algebraic characterization of finiteness. He also showed that a finite complex $X$ dominated by a finite $n$-complex $Y$ has the homotopy type of a finite $\operatorname{max}( 3 , n )$-complex if and only if a certain algebraic obstruction vanishes. ($X$ is dominated by $Y$ if the "homotopy of X survives passing through Y" , i.e. if there are mappings $f : X \rightarrow Y$, $g : Y \rightarrow X$ such that the composition $X \stackrel { f } { \rightarrow } Y \stackrel { g } { \rightarrow } X$ is homotopic to the identity). Whether "max3,n" can simply be replaced by "n" is still (1999) unanswered, due to difficulties when attempting to geometrically realize an algebraic $2$-complex.
In order to explain this in more detail, assume $B$ is a chain complex of free ${\bf Z} G$-modules,
\begin{equation*} B _ { 2 } \stackrel { d } { \rightarrow } B _ { 1 } \stackrel { d _ { 1 } } { \rightarrow } B _ { 0 } \rightarrow 0, \end{equation*}
where $B_0$ is freely generated by a single element $e_0$, $B _ { 1 }$ by $\{ e _ { 1 } ^ { i } \}$, $B _ { 2 }$ by $\{ e _ { 2 } ^ { j } \}$, $d _ { 1 } ( e _ { 1 } ^ { i } ) = g _ { i } e _ { 0 } - e _ { 0 }$ for some group element $g_i$, and $H _ { 1 } ( B ) = 0$, $H _ { 0 } ( B ) = \mathbf{Z}$. Wall asked if $B$ is necessarily the cellular chain complex of the universal covering $\widetilde { K }$ of a $2$-complex $K$ with fundamental group $G$. An affirmative answer would resolve the difficulties in dimension two mentioned above.
This topological set-up can also be rephrased in terms of combinatorial group theory. Let $F$ be the free group generated by $\{ x _ { i } \}$ and let $N$ be the kernel of the homomorphism from $F$ to $G$, sending $x_{i}$ to $g_i$. The image of the second boundary mapping $d _ { 2 }$ can be shown to be isomorphic to the relation ${\bf Z} G$-module $N / [ N , N ]$. Wall's question of geometric realizability now translates to asking whether the relation module generators $d _ { 2 } ( e _ { 2 } ^ { j } )$ lift to give a set of normal generators for $N$. This was answered negatively by M. Dunwoody (see [a39]).
Relation gap question.
M. Dyer showed that a more serious failure of this lifting problem, the relation gap question, would actually show that there does exist a finite $3$-complex dominated by a finite $2$-complex, with vanishing obstruction, that is not homotopically equivalent to a finite $2$-complex. Here, a finite presentation $F / N$ of a group $G$ is said to have a relation gap if no normal generating set of $N$ gives a minimal generating set for the relation module $N / [ N , N ]$. There have been many attempts to construct a relation gap in finitely presented groups (see [a4], p. 50). The existence of an infinite relation gap for a certain finitely-generated infinitely-related group was established in the influential paper of M. Bestvina and N. Brady [a1].
Eilenberg–Ganea conjecture.
Another problem revolving around geometric realizability, connected to the relation gap problem and the Whitehead conjecture, is the Eilenberg–Ganea conjecture. A group $G$ is of cohomological dimension $n$ if there exists a projective resolution of length $n$
\begin{equation*} 0 \rightarrow P _ { n } \rightarrow \ldots \rightarrow P _ { 0 } \rightarrow \mathbf{Z} \rightarrow 0 \end{equation*}
but no shorter one (see [a2] for a good reference on these matters). It was shown by S. Eilenberg, T. Ganea and J. Stallings ([a40], [a41]) that a group of cohomological dimension $n \neq 2$ admits an $n$-dimensional $K ( G , 1 )$ complex $K$. In particular, there is a geometric resolution of length $n$ arising as the augmented cellular chain complex of the universal covering of $K$.
The Eilenberg–Ganea conjecture states that this is true in dimension $2$ as well. This conjecture is widely believed to be wrong; promising potential counterexamples have been exhibited by Bestvina and also by Bestvina and Brady [a1]. If the group in question does not have a relation gap, then J.A. Hillman showed that a weaker version of the conjecture is true, see [a3]. In particular, if the group $G$ does not have a relation gap and acts freely and co-compactly on an acyclic $2$-complex, then it also admits a co-compact free action on a contractible $2$-complex.
A perhaps unsuspected connection between the Eilenberg–Ganea and the Whitehead conjecture was found by Bestvina and Brady in [a1]: at least one of the conjectures must be wrong!
References
| [a1] | M. Bestvina, N. Brady, "Morse theory and finiteness properties of groups" Invent. Math. , 129 (1997) pp. 445–470 |
| [a2] | K. Brown, "Cohomology of groups" , GTM , 87 , Springer (1982) |
| [a3] | J.A. Hillman, "2-knots and their groups" , Austral. Math. Soc. Lecture Notes 5 , Cambridge Univ. Press (1989) |
| [a4] | C. Hog-Angeloni, W. Metzler, A. Sieradski, "Two-dimensional homotopy and combinatorial group theory" , London Math. Soc. , 197 , Cambridge Univ. Press (1993) |
| [a5] | R. Kirby, "Problems in low-dimensional topology" W.H. Kazez (ed.) , Geometric Topology (1993 Georgia Internat. Topology Conf.) , 2 , Amer. Math. Soc. &Internat. Press (1993) pp. 35–473 |
| [a6] | D. Rolfsen, "Knots and links" , Publish or Perish (1976) |
| [a7] | C.P. Rourke, B.J. Sanderson, "Introduction to piecewise linear topology" , Springer (1972) |
| [a8] | J.J. Andrews, M.L. Curtis, "Free groups and handlebodies" Proc. Amer. Math. Soc. , 16 (1965) pp. 192–195 |
| [a9] | H. Tietze, "Ueber die topologische Invarianten mehrdimensionaler Mannigfaltigkeiten" Monatschr. Math. Phys. , 19 (1908) pp. 1–118 |
| [a10] | R.H. Crowell, R.H. fox, "Introduction to knot theory" , Ginn (1963) |
| [a11] | C.F. Miller, P.E. Schupp, Letter to M.M. Cohen , Oct. (1979) |
| [a12] | S. Akbulut, R. Kirby, "A potential smooth counterexample in dimension 4 to the Poincaré conjecture, the Schoenflies conjecture and the Andrews–Curtis conjecture" Topology , 24 (1985) pp. 375–390 |
| [a13] | R.E. Gompf, "Killing the Akbulut–Kirby sphere with relevance to the Andrews–Curtis and Schoenflies problems" Topology , 30 (1991) pp. 97–115 |
| [a14] | C.T.C. Wall, "Formal deformations" Proc. London Math. Soc. , 16 (1966) pp. 342–354 |
| [a15] | W. Metzler, "Aequivalenzaklassen von Gruppenbeschreibungen, Identitäten und einfacher Homotopietyp in niederen Dimensionen" , Lecture Notes London Math. Soc. , 36 , Cambridge Univ. Press (1979) pp. 291–326 |
| [a16] | C. Hog-Angeloni, W. Metzler, "Stabilization by free products giving rise to Andrews–Curtis equivalences" Note di Mat. , 10 : Suppl. 2 (1990) pp. 305–314 |
| [a17] | C. Hog-Angeloni, W. Metzler, "Andrews–Curtis Operationen mit höhere Kommutatoren der Relatorengruppe" J. Pure Appl. Algebra , 75 (1991) pp. 37–45 |
| [a18] | R. Kreher, W. Metzler, "Simpliziale Transformationen von Polyedren und die Zeeman-Vermutung" Topology , 22 (1983) pp. 19–26 |
| [a19] | P. Dierker, "Notes on collapsing $K \times I$ where $K$ is a contractible polyhedron" Proc. Amer. Math. Soc. , 19 (1968) pp. 425–428 |
| [a20] | W.B.R. Lickorish, "On collapsing $X ^ { 2 \times } I$" , Topology of Manifolds , Markham (1970) pp. 157–160 |
| [a21] | D. Gillman, "Bing's house and the Zeeman conjecture" Topology Appl. , 24 (1986) pp. 147–151 |
| [a22] | P. Wright, "Group presentations and formal deformations" Trans. Amer. Math. Soc. , 208 (1975) pp. 161–169 |
| [a23] | E.C. Zeeman, "On the dunce hat" Topology , 2 (1964) pp. 341–358 |
| [a24] | A. Zimmermann, "Eine spezielle Klasse kollabierbarere Komplexe $K ^ { 2 \times }I$" Thesis Frankfurt am Main (1978) |
| [a25] | M.M. Cohen, "Dimension estimates in collapsing $X \times I ^ { 2 }$" Topology , 14 (1975) pp. 253–256 |
| [a26] | M.M. Cohen, "Whitehead torsion, group extensions and Zeeman's conjecture in high dimensions" Topology , 16 (1977) pp. 79–88 |
| [a27] | D. Gillman, D. Rolfsen, "The Zeeman conjecture for standard spines is equivalent to the Poincaré conjecture" Topology , 22 (1983) pp. 315–323 |
| [a28] | S.V. Matveev, "Zeeman conjecture for unthickenable special polyhedra is equivalent to the Andrews–Curtis conjecture" Sib. Mat. Zh. , 28 : 6 (1987) pp. 66–80 (In Russian) |
| [a29] | O.S. Rothaus, "On the nontriviality of some group extensions given by generators and relations" Ann. of Math. , 106 (1977) pp. 599–612 |
| [a30] | J.H.C. Whitehead, "On adding relations to homotopy groups" Ann. of Math. , 42 (1941) pp. 409–428 |
| [a31] | W.H. Cockroft, "On two-dimensional aspherical complexes groups" Proc. London Math. Soc. , 4 (1954) pp. 375–384 |
| [a32] | J.F. Adams, "A new proof of a theorem of W.H. Cockroft" J. London Math. Soc. , 30 (1955) pp. 482–482 |
| [a33] | J. Howie, "Aspherical and acyclic $2$-complexes" J. London Math. Soc. , 20 (1979) pp. 549–558 |
| [a34] | J. Howie, "Some remarks on a problem of J.H.C. Whitehead" Topology , 22 (1983) pp. 475–485 |
| [a35] | J. Howie, "On the Asphericity of ribbon disc complements" Trans. Amer. Math. Soc. , 289 (1985) pp. 419–430 |
| [a36] | C.D. Papakyriakopoulos, "On Dehn's lemma and the asphericity of knots" Ann. of Math. , 66 (1957) pp. 1–26 |
| [a37] | G. Huck, S. Rosenbrock, "Eine verallgemeinerter Gewichtstest mit Anwendungen auf Baumpräsentationen" Math. Z. , 211 (1992) pp. 351–367 |
| [a38] | C.T.C. Wall, "Finiteness conditions for CW-complexes" Ann. of Math. , 81 (1965) pp. 56–69 |
| [a39] | J. Dunwoody, "Relation modules" Bull. London Math. Soc. , 4 (1972) pp. 151–155 |
| [a40] | S. Eilenberg, T. Ganea, "On the Lyusternik–Schnirelman category of abstract groups" Ann. of Math. , 46 (1945) pp. 480–509 |
| [a41] | J.R. Stallings, "On torsion-free groups with infinitely many ends" Ann. of Math. , 88 (1968) pp. 312–334 |
| [a42] | E.S. Rapaport, "Groups of order 1, some properties of presentations" Acta Math. , 121 (1968) pp. 127–150 |
Low-dimensional topology, problems in. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Low-dimensional_topology,_problems_in&oldid=56259