Freiheitssatz

independence theorem

A theorem originally proposed by M. Dehn in a geometrical setting and originally proven by W. Magnus [a1]. This theorem is the cornerstone of one-relator group theory.

The Freiheitssatz says the following: Let $G = \langle x _ { 1 } , \dots , x _ { n } : r = 1 \rangle$ be a group defined by a single cyclically reduced relator $r$. If $x_{1} $ appears in $r$, then the subgroup of $G$ generated by $x _ { 2 } , \dots , x _ { n }$ is a free group, freely generated by $x _ { 2 } , \dots , x _ { n }$.

In coarser language, the theorem says that if $G$ is as above, then the only relations in $x _ { 2 } , \dots , x _ { n }$ are the trivial ones.

The Freiheitssatz can be considered as a non-commutative analogue of certain more transparent results in commutative algebra. For example, suppose that $V = K ^ { n }$ is a linear space over a field $K$ with a basis $e _ { 1 } , \ldots , e _ { n }$. If $W = \operatorname { lin } ( w )$ is the subspace of $V$ generated by a vector $w = \sum _ { i = 1 } ^ { n } m _ { i } e _ { i }$ with $m _ { 1 } \neq 0$, then the elements $e _ { 2 } , \dots , e _ { n }$ are linearly independent modulo $W$.

Magnus' method of proof of the Freiheitssatz relies on amalgamations (cf. also Amalgam; Amalgam of groups). This method initiated the use of these products in the study of infinite discrete groups.

One of the by-products of Magnus' proof was an extraordinary description of the structure of these groups, which allowed him to deduce that one-relator groups have solvable word problem (cf. also Identity problem; [a2]).

There are two general approaches to extending the Freiheitssatz. The first is concerned with the notion of the one-relator product $G = * A _ { i } / N ( r )$ of a family $\{ A _ { i } \}$ of groups, where the element $r$ is cyclically reduced and of syllable length at least $2$ and $N ( r )$ is its normal closure in $* A_i$. Some authors (see [a3]) give conditions for the factors $A_i$ to inject into $G$.

The second approach is concerned with multi-relator versions of the Freiheitssatz (see [a3] for a list of references). For example, the following strong result by N.S. Romanovskii [a4] holds: Let 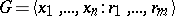have deficiency $d = n - m > 0$. Then there exist a subset of $d$ of the given generators which freely generates a subgroup of $G$.

References

[a1]	W. Magnus, "Über discontinuierliche Gruppen mit einer definierenden Relation (Der Freiheitssatz)" J. Reine Angew. Math. , 163 (1930) pp. 141–165
[a2]	W. Magnus, "Das Identitätsproblem für Gruppen mit einer definierenden Relation" Math. Ann. , 106 (1932) pp. 295–307
[a3]	B. Fine, G. Rosenberger, "The Freiheitssatz and its extensions" Contemp. Math. , 169 (1994) pp. 213–252
[a4]	N.S. Romanovskii, "Free subgroups of finitely presented groups" Algebra i Logika , 16 (1977) pp. 88–97 (In Russian)